太阳同步圆轨道空间相机瞬态外热流计算
2012-10-30刘巨
刘 巨
(中国科学院 长春光学精密机械与物理研究所,吉林 长春130033)
1 引 言
空间相机,尤其是外接于卫星平台的空间相机受到的空间热环境影响与航天器一样,主要为空间外热流的作用。但空间相机对温度范围的要求往往比航天器高很多,其控温精度范围仅为“几度”。因此,作为空间相机的热边界条件,其外热流计算应更为精细,尤其对相机通光孔所在的对地面,应考虑外热流对相机内部温度环境的影响,对其进行外热流的瞬态变化情况分析,以进行空间相机的适应性热设计。
目前,空间外热流的计算已经有较成熟的算法。文献[1-4]对航天器外热流计算方法进行了详尽的论述,并编制了相应的程序,但这些程序均未成体系,还限于研发阶段的探索,无法进行实际应用。国际上一些空间外热流计算商业程序软件较为成熟,如NEVADA、IDEAS/TMG 等,国内一些研究机构已引进这些软件,并应用于实际工程设计中。
针对太阳同步圆轨道,本文给出了空间定位的理论算式及必要参数。采用STK 软件进行了轨道与太阳相对位置关系( β 角) 的计算,进而对外热流综合能量最大和最小的轨道进行了空间定位,确定了轨道环境的高、低温工况。以外接于卫星平台的空间相机为例,采用IDEAS/TMG 模块对高、低温工况轨道周期内的瞬态外热流变化进行了详细的分析计算,结果可为空间相机的热分析计算及地面热试验外热流的模拟提供输入条件。
2 太阳同步圆轨道的定位问题
2.1 卫星的空间定位
在以地球中心为原点的赤经、赤纬坐标系中,卫星所处轨道位置由6 个轨道根数决定,即卫星轨道半长轴a、卫星轨道偏心率e、卫星轨道面与地球赤道面的倾角i、轨道升交点赤经Ω( 由春分点到升交点的地心角距) 、近地点幅角ω( 升交点到轨道近地点的角距) 、平近点角M( 卫星从近地点开始按平均轨道角速度运动转过的角度) 。其中,a、e是确定轨道大小和形状的根数,i、Ω 和ω是轨道平面和长半轴的空间定向根数,M为时间根数。6 个轨道根数满足下述关系[5-6]:

其中: r 为卫星位置矢量,E为偏近点角( 近地点和卫星对轨道长轴垂线的反向延长线与椭圆外切圆的交点之间的圆心角距) 。由此关系式即可解出任何时刻卫星的空间位置,即星历计算。
2.2 太阳同步圆轨道的空间定位
太阳同步轨道与黄道上太阳移动同步,轨道平面将每天向西移动0.986°,产生一条倒退轨道。太阳同步轨道每天经过赤道和各个纬度的时间都相同,由此可知,太阳同步轨道每个轨道周期的降交点地方时均相同。对于给定的太阳同步圆轨道,6 个轨道根数中的a,e,i,ω 为已知常数,即e,ω 为常数0,轨道半长轴a为轨道半径,i为轨道倾角。而M为轨道的时间根数,如果不考虑卫星在轨道周期内的时间历程,则可以得出结论:对于太阳同步圆轨道,升交点赤经Ω 是轨道空间定位的唯一待定参数。
由于太阳同步轨道的降交点地方时不变,在实际应用中,定义太阳同步圆轨道常常给出的必要参数为轨道高度a和降交点地方时,而对太阳同步轨道的某一圈轨道定位一般都采用升交点赤经Ω 进行。
3 太阳同步圆轨道空间相机瞬态外热流计算
进行空间外热流瞬态计算时,整个寿命周期内的瞬态外热流变化情况是难以实现的,要根据“极端”原则找出外热流综合能量最大和最小的轨道,对此两个轨道的外热流能量进行分析计算,得出寿命周期内外热流综合能量的最大值和最小值,可以认为,整个寿命周期内的外热流能量在最大值与最小值的范围内变化。
空间外热流主要有太阳辐射热流Q1、地球太阳反照热流Q2、地球红外辐射热流Q33 个部分。Q3仅与轨道高度有关,寿命周期内变化不大,因此空间外热流的变化主要体现在Q1与Q2的变化上,而Q1与Q2的变化是由于太阳在黄道上进行周期运动造成太阳与卫星轨道面夹角( β 角) 在一定范围内不断变化产生的结果。由此可知,卫星在轨运行期间轨道外热流综合能量的变化取决于太阳与轨道面的夹角—β 角。β 角越大,轨道外热流综合能量就越大,反之则越小,外热流综合能量变化正比于sin β。
经上述分析可知,太阳同步圆轨道瞬态外热流计算应分为两个步骤:
(1) 进行轨道与太阳位置的关系( β 角) 计算,由此确定外热流综合能量最大和最小的轨道;
(2) 对外热流综合能量最大和最小的轨道进行瞬态外热流的分析计算。
3.1 轨道与太阳的相对位置关系( β 角)计算
β 角计算公式[7]如下:
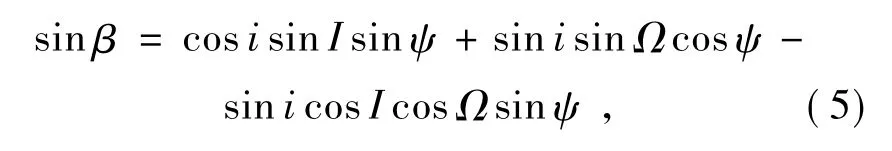
式中:i为轨道倾角,I为赤道面与黄道面的夹角,Ω 为升交点赤经,ψ 为太阳黄经。
实际工作中,往往采用稳定可靠的计算程序进行β 角计算,本文采用STK 软件进行β 角计算。假设太阳同步圆轨道参数为:
(1) 轨道高度:800 km;
(2) 降交点地方时:10∶00。
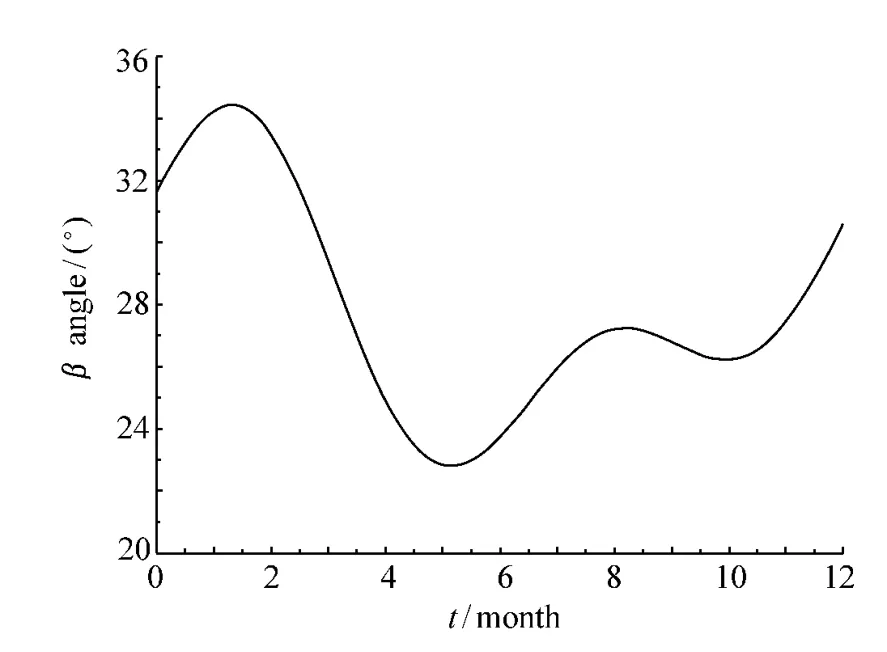
图1 一年内β 角变化曲线Fig.1 β angle curve in one year
经计算,得出一年内β 角变化曲线,如图1 所示。β 角极值及对应的日期和相应升交点赤经Ω值见表1。

表1 β 角极值情况Tab.1 Extra values of β angles
由此,定位出外热流综合能量最大值和最小值对应的两条轨道,即升交点赤经Ω 为109.5°和224.9°对应的两条轨道,通常把这两条轨道定义为高温和低温工况轨道。
3.2 瞬态外热流计算
空间外热流的算法已经比较成熟,都是将卫星划分为微元或单元进行计算,然后积分或求和。卫星外表面任一微元dA接收到的太阳辐射外热流dq1、地球太阳反照外热流dq2、地球红外辐射外热流dq3计算公式[7-8]分别如下:
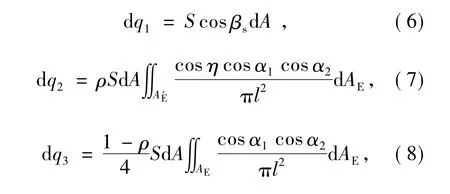
式中:S为太阳常数,βs为dA法线方向与太阳光矢量夹角,ρ 为地球太阳平均反照率,dAE为地球表面微元,A'E为受到太阳直接照射的地球表面面积,η 为dAE法线方向与太阳光矢量夹角,α1为dAE法线方向与dA-dAE连线夹角,α2为dA法线方向与dAE-dA连线夹角,l为dA到dAE之间的距离。
实际工作中,仍然要采用稳定可靠的计算程序进行外热流的计算。计算的输入条件除定位好的轨道外,还必须确定空间外热流物理参数,即太阳常数、地球太阳平均反照率、地球表面平均红外辐射密度。这3 个参数一年之间也在一定范围内变化,同样根据“极端”原则,在进行高、低温工况轨道外热流计算时,分别取较大值和较小值。
这里需要注意的是,根据β 角极值选定的高、低温工况轨道实际的外热流物理参数并不一定是最大或最小值。因此在计算中采用了“双重极端”原则,即在β 角最大的高温工况轨道选用外热流物理参数的极大值,在β 角最小的低温工况轨道选用外热流物理参数的极小值,这样就能确保整个寿命周期内的外热流能量变化在此两种工况下计算的外热流能量范围内。外热流物理参数选取[7]见表2。

表2 外热流物理参数Tab.2 Physical parameters of space heat fluxes
假设某空间相机外接于卫星平台,工作于前述假设的太阳同步圆轨道,相机对地定向,外包络尺寸为1.1 m×1.1 m ×1.5 m 的立方体,卫星平台为1.5 m×1.5 m×1.5 m 的立方体。太阳帆板在卫星飞行方向两侧,展开尺寸为4 m ×1.5 m。采用IDEAS 软件相关模块划分有限单元并进行表面属性赋值,建模后的外热流计算模型见图2,模型表面属性参数见表3。这里需要指出,为方便进行相机热分析计算及地面环境试验模拟工作,通常进行相机到达外热流的分析计算,因此将相机外包络表面假想为“黑”表面。
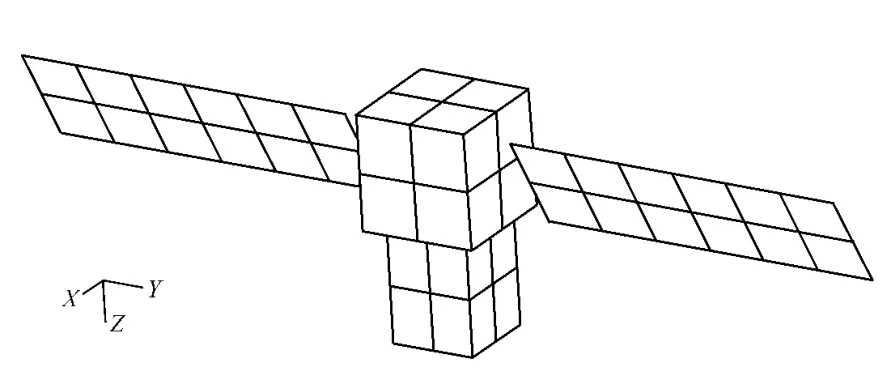
图2 外热流计算模型Fig.2 Calculation model of space fluxes
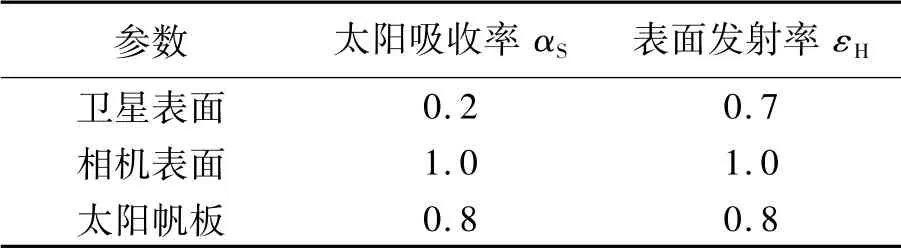
表3 模型表面属性参数Tab.3 Surface attribute parameters ofcalculation model
采用IDEAS/TMG 模块进行轨道建模及外热流计算。该模块进行轨道外热流计算时,通常将指定轨道分成若干等分,计算各等分位置的外热流,瞬态外热流变化则是根据各等分点外热流值拟合后得出的结果。在实际计算中,由于卫星进出“地影”时外热流能量变化较大,因此IDEAS/TMG 模块除计算各等分点外热流值之外,在卫星进出“地影”位置各计算两个点,这样使外热流拟合结果更为准确。
按照前述轨道参数,采用IDEAS/TMG 模块进行轨道建模,将轨道分成24 等分,实际计算28个点的外热流,然后进行数据拟合。由于计算结果较多,算例中,仅对相机对地面( 计算模型中的+Z方向) 的瞬态到达外热流进行分析计算,其它各面结果不一一列出。
经计算,高温工况轨道相机+Z面到达外热流变化曲线如图3 所示,低温工况轨道相机+Z面到达综合外热流变化曲线如图4 所示。两种工况计算起始位置均为当圈轨道升交点。相机+Z面轨道周期平均到达外热流计算结果见表4。

图3 高温工况轨道相机+Z 面到达外热流的变化Fig.3 Transient change curves of space heat fluxes of +Z surface in upper temperature orbit
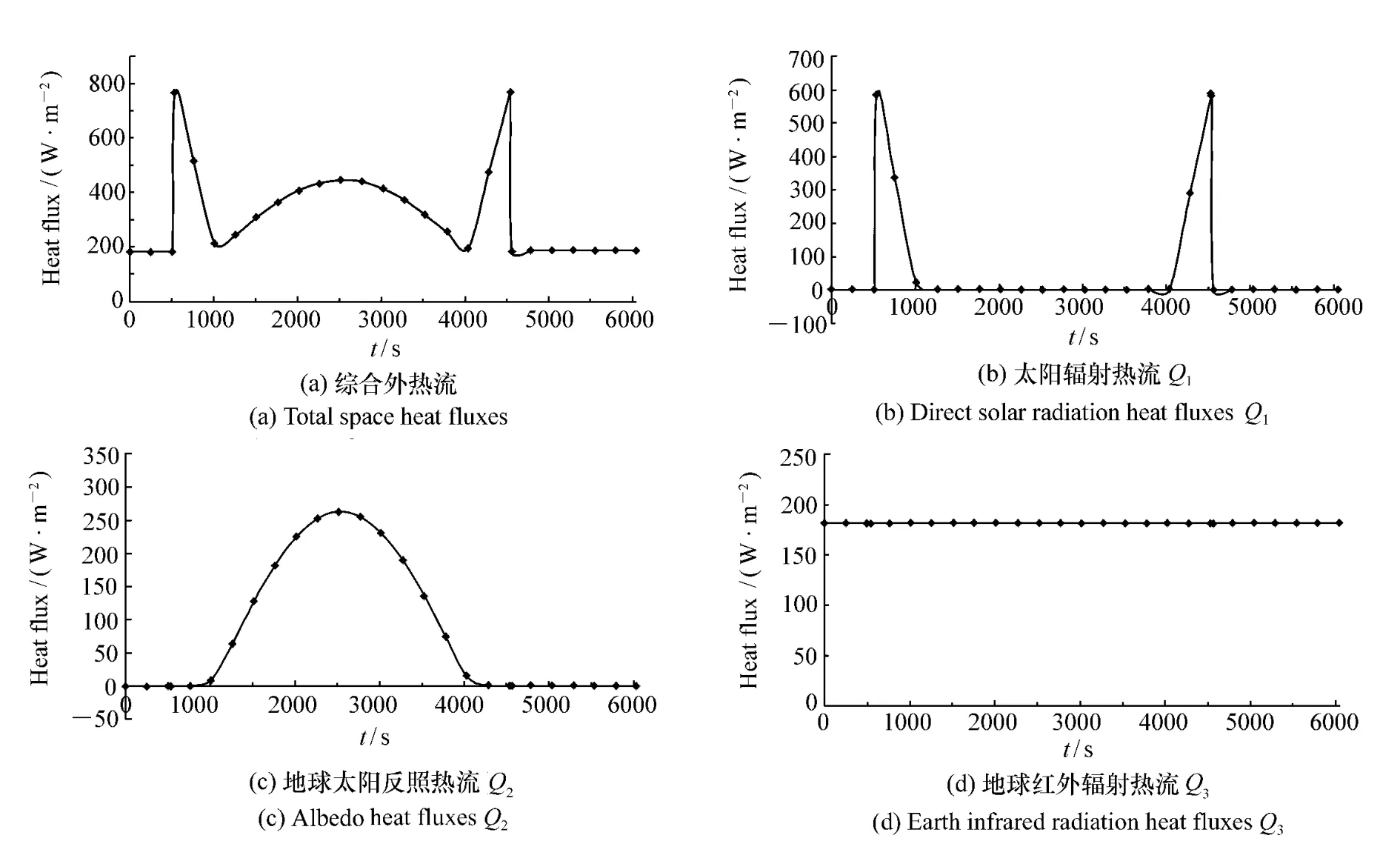
图4 低温工况轨道相机+Z 面到达外热流的变化Fig.4 Transient change curves of space heat fluxes of +Z surface in lower temperature orbit
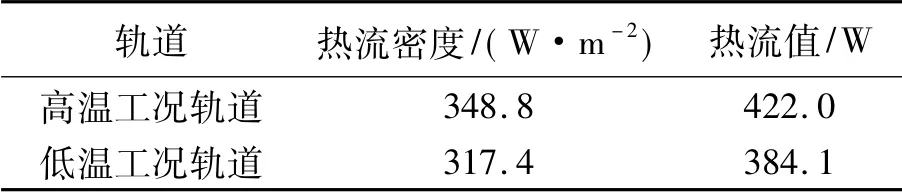
表4 相机+Z 面轨道周期平均到达外热流Tab.4 Orbit period averaged space heat fluxes of +Z surface
由以上计算结果不难得出一些结论,如:地球红外辐射热流在轨道周期内不变; 相机对地面进出地影区域受阳光直射; 高低温工况卫星进出地影的时间不同;以及Q1,Q2,Q3的变化范围等等,这里不多赘述。
4 结 论
本文从理论角度出发,结合软件应用,详细论述了太阳同步圆轨道空间相机瞬态外热流计算的整个过程。计算结果得出了相机各面的到达外热流及计算工况轨道周期内的瞬态变化情况,可以作为空间相机热设计、热分析的边界条件,也可以为空间相机地面热试验边界条件的模拟提供数据;对空间相机热分析和热试验的深入研究—空间相机在轨瞬态温度场预示和地面模拟空间环境的瞬态热平衡试验也具有重要的意义。
[1] 李万林.卫星空间外热流轨道参数ψ0、Ω0和ω0计算[J].中国空间科学技术,1993,13(6) :58-61.LI W L. Calculation of orbital parameters ψ0,Ω0and ω0used for calculating space heat flux[J].Chinese Space Sci. Technol.,1993,13(6) :58-61.( in Chinese)
[2] 翁建华,潘增富,闵桂荣.空间任意形状凸面的轨道空间外热流计算方法[J].中国空间科学技术,1994,14(2) :11-18.WENG J H,PAN Z F,MIN G R. A method of calculating external heat fluxes on arbitrary shaped convex surface of spacecraft[J].Chinese Space Sci. Technol.,1994,14(2) :11-18.( in Chinese)
[3] 翁建华,潘增富,闵桂荣.任意形状凹面和相互可视表面φ2、φ3的分析计算[J].中国空间科学技术,1994,14(3) :9-16.WENG J H,PAN Z F,MIN G R. Calculating orbital heat fluxes of concave surfaces and mutually visible surfaces with specula reflection[J].Chinese Space Sci. Technol.,1994,14(3) :9-16.( in Chinese)
[4] 赵立新.轨道空间外热流计算的一种新方法[J].光学 精密工程,1995,3(6) :80-85.ZHAO L X. A new method to calculate the heat flux in spacecraft orbits[J].Opt. Precision Eng.,1995,3(6) :80-85.( in Chinese)
[5] 刘林,胡松杰,王歆.航天动力学引论[M].南京:南京大学出版社,2006.LIU L,HU S J,WANG Y.An Introduction of Astrodynamics[M]. Nanjing: Nanjing University Express,2006. ( in Chinese)
[6] 郗晓宁,王威.近地航天器轨道基础[M].北京:国防科技大学出版社,2003.XI X N,WANG W.Fundamentals of Near-earth Spacecraft Orbit[M]. Beijing:National University of Defense Technology Press,2003.( in Chinese)
[7] 闵桂荣.卫星热控制技术[M].北京:宇航出版社,1991.MIN G R.Thermal Control Technique of Satellite[M]. Beijing:Astronautics Press,1991.( in Chinese)
[8] 闵桂荣,郭舜.航天器热控制[M].2 版.北京:科学出版社,1998.MIN G R,GUO SH.Thermal Control of Spacecraft[M]. 2nd ed. Beijing:Science Press,1998.( in Chinese)
