面料力学性能与结构性能的相关性分析
2012-10-29沈璐
沈 璐
(东华大学服装学院,上海 200051)
在服装生产过程中,面料的力学性能很大一部分决定了成衣的效果和质量,也是服装的成衣加工性能的客观体现,因此服装面料力学性能的研究已经成为目前纺织服装科研方面的一大主题。 同时面料结构参数也是影响成衣效果的重要指标,因此,企业为了提高生产的准确性,迫切需要得到有关服装面料结构参数与力学性能参数的关系作为客观参考,以适应市场需要。 本文对面料力学性能与结构性能的相关性作了分析。
1 结构参数主成分因子提取
针对误差剔除和筛选后的120种织物面料,做了相关的结构参数测量,得出其厚度、克重、经密和纬密几种结构性能参数,同时以厚度与克重的比值作为一种新的性能表达指标,间接表达织物紧度。
针对织物结构性能参数进行SPSS相关性分析得出,织物厚度、克重、织物厚克比值以及织物经密、纬密,都表现显著的相关性,其中织物厚克比值与织物厚度和克重表现出显著的正相关性,与织物经密和纬密表现出显著的负相关,故可以求取织物厚克比值与其他几个变量直接之间的回归关系,以织物厚克比值作为反映织物结构性能的综合性因子,回归分析结果见表1。

表1 模型拟合过程
表1中R2表示自变量xi与因变量y之间线性关系密切程度的指标,取值范围在0~1之间,其值越接近1,表示线性关系越强。为消除自变量的个数以及样本量的大小对判定系数的影响,这里引入修正后的R2,作为回归模拟优劣的评价指标。由表中和修正的值可以看出,R2和修正后的R2之间的差异性很小,即建立的回归方程比较好。
方差分析表显示回归拟合过程中每一步的方差分析结果。Sig为F值大于F临界值得概率,表1中结果表明,当回归方程包含不同的自变量时,其显著性概率值均小于0.001,即拒绝回归系数均为0的原假设[2],因此,最终的回归方程应该包括这4个自变量,且方程拟合效果很好。
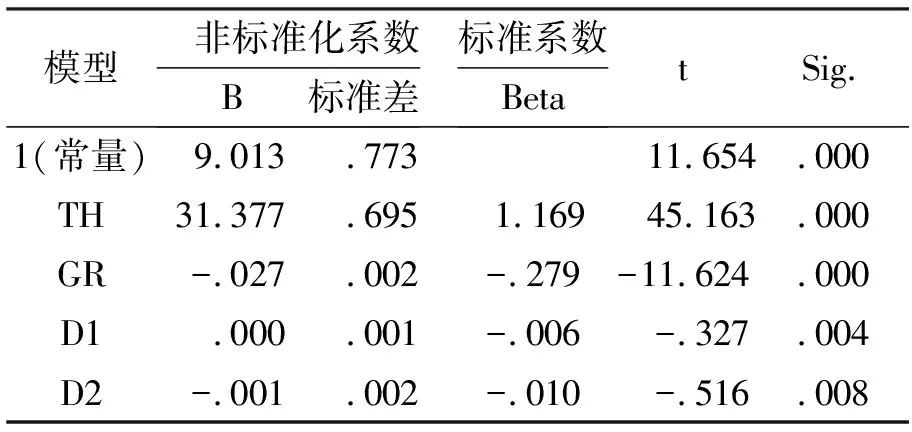
表2 回归分析因子系数表
备注:TH—织物厚度,GR—织物单位面积克重,TH/GR—织物厚克比值,D1—织物经密,D2—织物纬密。因变量:TH/GR。
由表2得知,B为结构性能主成分因子与力学性能主成分因子之间的回归系数,Sig值表示的是回归系数的优化程度,此值越接近于0,说明回归拟合度越好,表中每个主成分因子对应的Sig值都小于0.05,即织物厚克比值参数与其他结构性能因子的回归线性拟合度都较好。因此织物厚克比值与厚度、克重、经密和纬密间的回归关系方程可以写为:
TH/GR=9.013+31.377×TH-0.027×GR-0.001×D2
(1)
为验证主成分因子获取的正确性以及其表达信息的准确性与完整性,对织物厚克比值与各结构变量进行散点图线性模拟,得出厚克比值与各结构自变量之间具有高度的线性相关性,即织物厚克比值这一新生成的变量指标完全可作为以表达织物结构性能的综合性指标。
2 力学参数主成分因子提取
本文尽可能多的选择多种物理力学性能指标,并采用多元线性逐步回归来计算出织物的风格值,得出各种物理力学性能指标对织物质量和风格的影响程度,并通过一种全面、整体、科学的表达式来定量表达;从中找出影响织物质量和风格的主要物理力学性能指标[3]。本文中面料力学性能参数是通过KES织物风格测试仪分别对各种织物的表面性能参数、弯曲性能参数、剪切性能参数、拉伸性能参数、织物克重、织物厚度以及织物经纬密等相关参数进行测量;以此应力下的力学性能参数来更加准确表征服装面料穿着时的效果[4]。
根据仪器对样品的损伤程度,即拉伸>剪切>弯曲>压缩>表面摩擦,安排样品力学性能测试顺序:表面摩擦→压缩→弯曲→剪切→拉伸;实验采取同种实验相同部位测量三次求均值的方法,以减少测量误差,其中拉伸性能、剪切性能、弯曲性能和表面摩擦性能有经纬向之分,采取经向、纬向各测试三次求其均值,以更加准确的表征面料的风格性能。
材料准备:首先对分类后选取的120种织物面料进行预缩和熨烫,针对预缩和熨烫完成后的面料进行试验样片准备,每种面料在距布边10 cm内取样,以20 cm×20 cm的规格裁剪6块样品,并且一条边与经向平行,标清面料分类及编号和经纬方向,然后在恒温恒湿实验室中放置24 h以上,以便面料样品在标准环境下有足够的时间恢复至自然伸展状态,以减小因环境因素对实验结果造成的偏差;按顺序进行测试。
由相关性分析可得出:弯曲性能与剪切性能、压缩能量、压缩回弹性和拉伸性能都表现出显著的相关性;剪切性能与弯曲性能和拉伸性能表现出显著的相关性;压缩性能与弯曲性能和拉伸性能表现出显著的相关性;拉伸性能与弯曲性能、剪切性能、压缩能量和压缩回弹性表现出显著的相关性;并且除经、纬向表面摩擦系数平均偏差MMD数据显示出较明显的不相关性之外,其他同一类参数下经、纬向数据均表现出显著的相关性,因此这里将相关性显著的经、纬向数据进行用均值表示此参数的综合性能。
对使用均值表征的面料综合性能数据进行因子分析及主成分分析,得出6种主成分,由分析得出总共有6组数据变量的累计贡献率达到了90%以上,故获取6个新的变量作为表达所有织物风格信息的6个主成分,给其命名分别为Factor1、Factor2、Factor3、Factor4、Factor5、Factor6。
3 结构性能与力学性能参数相关性模型的建立
针对织物结构性能参数中所提取的织物厚克比值和力学性能参数中所提取的六个主成分因子,论文进一步使用SPSS数据分析软件对其进行多元线性回归分析,寻找其间的线性关系,并对其间的线性关系进行线性模拟。

表3 模型拟合过程
注:预测值:(常量),Factor1, Factor2, Factor3, Factor4, Factor5, Factor6。因变量:TH/GR。
表3中使用了反映自变量与因变量之间线性关系密切程度的指标R2和修正后的R2来判定因变量和自变量线性回归模拟的拟合优度,以更加准确地反映线性模拟效果;由表中和修正的值可以看出,R2和修正后的R2之间的差异性很小,即建立的回归方程比较好。
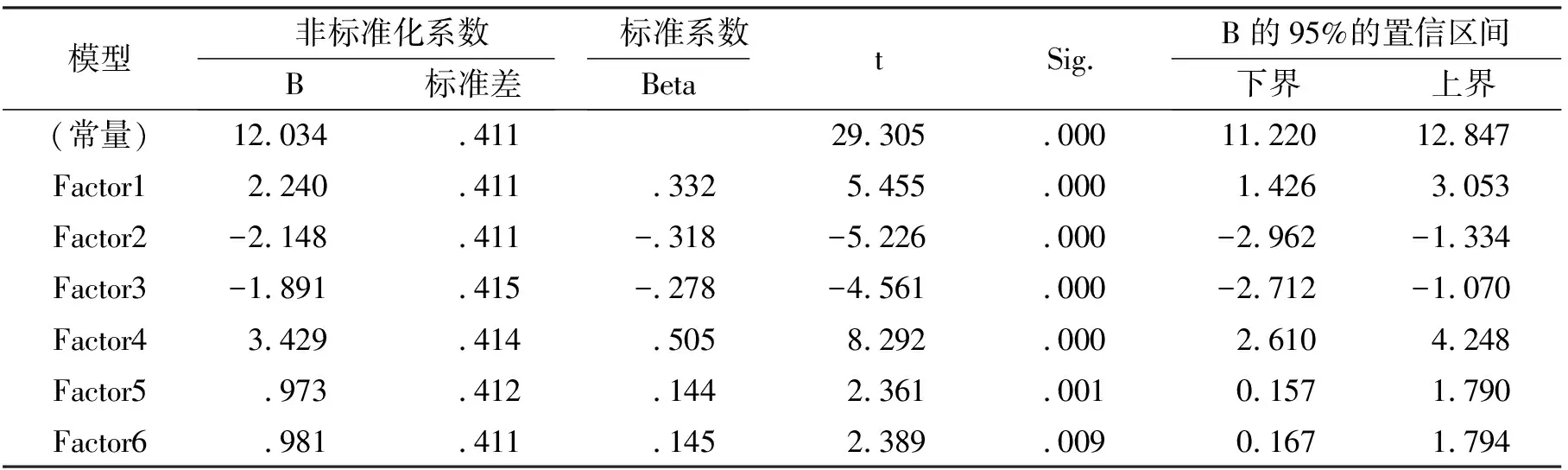
表4 回归分析因子系数表
由表4得知,B为结构性能因子与力学性能主成分因子之间的回归系数,Sig值表示的是回归系数的优化程度,此值越接近于0,说明回归拟合度越好,表中每个主成分因子对应的Sig值都小于0.05,即每个力学主成分因子与结构性能因子的回归线性拟合度都较好。因此织物结构性能与力学性能回归关系方程可以写为:
TH/GR=12.034+2.240×Factor1-2.148×Factor2-1.891×Factor3+3.429×Factor4+0.973×Factor5+0.981×Factor6
(2)
4 结论
本文选取企业常用面料,在实验基础上用SPSS进行数据分析,建立了各类面料主成分因子与织物结构性能间的相关性模型。实现了目前企业对面料性能客观性评价的需求,为以后新开发面料以及投放市场打下了基础。
[1] 卢纹岱.SPSS统计分析[M].第4版.北京:电子工业出版社.2010.
[2] 庄楚强,何春雄.应用数理统计基础[M].第3版.广州:华南理工大学出版社.2006.
[3] 陈丽,许树文,张国君.西服面料与粘合衬配伍效果的评判模型[J].浙江纺织服装职业技术学院学报,2006 (1):13-21.
[4] 张金瑞.轻薄毛精纺面料与双点粘合衬的配伍性研究[D].上海:东华大学,2005:12-14.
