数学家与π

黑龙江 张艳 姜彦琪

数学家与π

黑龙江 张艳 姜彦琪

圆周率是表示圆的周长与直径的比的一个定值。本文通过介绍古今中外著名数学家探索其准确近似值的过程，从而展现π的魅力以及数学方法的奇异美。

圆周率；阿基米德；刘徽；祖冲之

引言

圆周率是一个极其驰名的数。从有文字记载的历史开始，这个数就引起了外行人和学者们的兴趣。作为一个非常重要的常数，圆周率最早是出于解决有关圆的计算问题。圆的周长总是直径的3倍多一些，表示这3倍多一些的数是一个固定的数，我们把圆的周长和直径的比值称之为圆周率。用字母π表示。圆周率是一个无限不循环小数，也就是说它的小数部分既是无限的又是无规律的，是永远写不完的。回顾历史，我们可以将这一计算历程分为几个阶段。

1 实验时期

通过实验对π值进行估算，这是计算π的的第一阶段。估算基本上都是以观察或实验为根据，是基于对一个圆的周长和直径的实际测量而得出的。大约公元前2000年，古巴比伦人用近似值3.125表示π。在古代世界，实际上长期使用π＝3这个数值。最早见于文字记载的有基督教《圣经》中的章节。在我国刘徽之前“圆径一而周三”曾广泛流传。我国第一部《周髀算经》中就有记载。木工师傅有两句从古流传下来的口诀：叫做：“周三径一，方五斜七”，意思是说，直径为1的圆，周长大约是3，边长为5的正方形，对角线之长约为7。这正反映了早期人们对圆周率π和这两个无理数的粗略估计。东汉时期官方还明文规定圆周率取3为计算面积的标准。后人称之为“古率”。早期的人们还使用了其它的粗糙方法。如古埃及、古希腊人曾用谷粒摆在圆形上，以数粒数与方形对比的方法取得数值。或用匀重木板锯成圆形和方形以秤量对比取值……由此，得到圆周率的稍好些的值。如古埃及人应用了约四千年的4(8/9)2=3.1605。

2 几何法时期

阿基米德在一篇论文《圆的测定》中第一次创用上、下界来确定π的近似值，他使用了基于内接和外切多边形的几何方法证明了“圆周长与圆直径之比小于3+(1/7)而大于3+(10/71)”，得到了上下界：3.1408＜π＜3.1428。到公元150年左右，希腊天文学家托勒密得出π＝3.1416，取得了自阿基米德以来的巨大进步。

在我国，首先是由数学家刘徽得出较精确的圆周率。公元263年前后，刘徽提出著名的割圆术，得出π＝3.14，通常称为“徽率”，他指出这是不足近似值。虽然他提出割圆术的时间比阿基米德晚一些，但其方法确有着较阿基米德方法更美妙之处。割圆术仅用内接正多边形就确定出了圆周率的上、下界，简捷很多。另外，有人认为在割圆术中刘徽提供了一种绝妙的精加工办法，以致于他将割到192边形的几个粗糙的近似值通过简单的加权平均，竟然获得具有4位有效数字的圆周率π＝3927/1250＝3.1416。而这一结果，如果通过割圆计算，需要割到3072边形。这一神奇的精加工技术是割圆术中最为精彩的部分，令人遗憾的是，由于人们对它缺乏理解而被长期埋没了。

恐怕大家更加熟悉的是祖冲之所做出的贡献，祖冲之关于圆周率的两大贡献。其一是求得圆周率3.1415926＜π＜3.1415927。其二是，得到π的两个近似分数即：约率为22／7；密率为355／113。他算出π的8位可靠数字，不但在当时是最精密的圆周率，而且保持世界记录九百多年。以致于有数学史家提议将这一结果命名为“祖率”。

1150年，印度数学家婆什迦罗第二计算出π=3927/1250=3.1416。1424年，中亚细亚地区的天文学家、数学家卡西著《圆周论》，计算了3×228＝805,306,368边内接与外切正多边形的周长，求出π值，他的结果是：π＝3.14159265358979325有十七位准确数字。这是国外第一次打破祖冲之的记录。16世纪的法国数学家韦达利用阿基米德的方法计算π近似值，用6×216正边形，推算出精确到9位小数的π值。他采用比阿基米德更先进的工具：十进位置制。17世纪初，德国人鲁道夫用了几乎一生的时间钻研这个问题。他也将新的十进制与早的阿基米德方法结合起来，但他是从正方形开始的，一直推导出了有262条边的正多边形，约4,610,000,000,000,000,000边形！这样，算出小数35位。为了记念他的这一非凡成果，在德国圆周率π被称为“鲁道夫数”。但是，用几何方法求其值，计算量很大，它已引导数学家们走得很远，再向前推进，必须在方法上有所突破。

3 分析法时期

这一时期人们开始摆脱求多边形周长的繁难计算，利用无穷级数或无穷连乘积来1593年，韦达给出

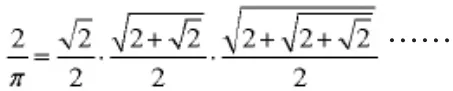
这一不寻常的公式是π的最早分析表达式。它表明仅仅借助数字2，通过一系列的加、减、乘、除和开平方就可算出π值。接着有多种表达式出现。如沃利斯1650年给出：

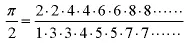
1706年，梅钦建立了一个重要的公式，现以他的名字命名

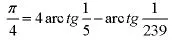
再利用分析中的级数展开，他算到小数后100位。显然，级数方法宣告了古典方法的过时。此后，对于圆周率计算的纪录一个接着一个：1844年，达塞利用公式：

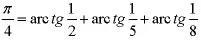
算到了200位。19世纪以后，类似的公式不断涌现，π的位数也迅速增长。1873年，谢克斯利用梅钦的一系列方法，算到小数后707位。这一惊人的结果成为此后74年的标准。此后半个世纪，人们对他的计算结果深信不疑，或者说即便怀疑也没有办法来检查它是否正确。以致于在1937年巴黎博览会发现馆的天井里，依然显赫地刻着他求出的π值。又过了若干年，数学家弗格森对他的计算结果产生了怀疑，其疑问基于如下猜想：在π的数值中，各数码出现的机会应该相同。当他对谢克斯的结果进行统计时，发现各数字出现次数过于参差不齐。1946年，弗格森发现从第528位开始是错的（应为4，误为5）。直到1948年1月弗格森和伦奇两人共同发表有808位正确小数的π。这是人工计算π的最高记录。

4 计算机时期

1946年，世界第一台计算机ENIAC制造成功，标志着人类历史迈入了电脑时代，导致了计算方面的根本革命。1949年，ENIAC根据梅钦公式计算到2035（一般说是2037）位小数，包括准备和整理时间在内仅用了70小时。计算机的发展一日千里，其记录也就被频频打破。

5 结束语

现在打破记录，不管推进到多少位，也不会令人感到特别的惊奇了。实际上，把π的数值算得过分精确，应用意义并不大。现代科技领域使用的π值，有十几位已经足够。如果用鲁道夫的35位小数的π值计算一个能把太阳系包围起来的圆的周长，误差还不到质子直径的百万分之一。我们还可以引美国天文学家西蒙·纽克姆的话来说明这种计算的实用价值：“十位小数就足以使地球周界准确到一英寸以内，三十位小数便能使整个可见宇宙的四周准确到连最强大的显微镜都不能分辨的一个量。”那么为什么数学家们还象登山运动员那样，奋力向上攀登，一直求下去而不是停止对π的探索呢？为什么其小数值有如此的魅力呢？通过几何、微积分、概率等广泛的范围和渠道发现π竟然与这么些表面看来风马牛不相及的试验，沟通在一起，这的确使人惊讶不已，这充分显示了数学方法的奇异美。

[1]张顺艳.数学的源与流.高等教育出版社，2003.

[2]刘耀，赵敦.趣谈高等数学.兰州大学出版社，2000.

[3]李心灿.高等数学应用205例.北京：高等教育出版社，1997.

[4]刘耀，徐军民，陈知先.新编高等数学（第一册）.兰州大学出版社，1988.

[5]b·B鲍尔加尔斯基著，潘德松，沈金钊译.数学简史.知识出版社，1984.

[6]韩雪涛.计算圆周率.http://www.pep.com.cn/200503/ca.669359.htm，2003.

（编辑 李艳华）

（作者单位：牡丹江市卫生学校）