关于Pell方程x2-(4n+2)y2=-1的解的几个判别方法
2012-10-27杜先存赵金娥
杜先存,赵金娥
(红河学院a.教师教育学院,b.数学系,云南蒙自 661199)
通常的Pell方程指形如x2-Dy2=±1或x2-Dy2=±4(x,y∈Z,D 是一个非完全平方的正整数)的不定方程.广义的Pell方程是上述形式的推广,它具有以下两种基本形式:
x2-Dy2=C(x,y,C∈Z,D 是一个非完全平方的正整数);
ax2-by2=±1或±2或±4(x,y∈Z,ab∈Z+,a,b是非完全平方的正整数).
Pell方程经过许多人的研究,不仅在理论上已日臻成熟,而且其应用价值也在不断被挖掘.在现实生活中,关于Pell方程的应用也非常广泛,在其他一些领域,如计算机科学、电子学、信号的数字处理等方面,也应用到Pell方程的相关知识.Pell方程的理论成果在丢番图逼近理论及代数数论中起着十分重要的作用,并且对于解决一类丢番图方程解的存在性问题有着很大的帮助.
关于广义Pell方程x2-Dy2=C的解的问题,文献[1]已有一些结果.关于广义Pell方程ax2-by2=1的解的问题,文献[2]已有一些结果.关于Pell方程

的整数解的问题,文献[3-5]已有如下结果:
定理1′[3]当D≡1(mod 4)时,(*)有整数解.
定理2′[4]当≡5(mod 8)且为素数时,(*)有正整数解.
定理3′[5]当D≡3(mod 4)或D 含 有4m+3型素因子时,(*)无整数解.
定理4′[5]当D≡0(mod 4)时,(*)无整数解.
定理5′[5]当≡1(mod 8)且为素数时,若D=r2+s2(其中r、s为奇数),如果r≡±3(mod 8),s≡±3(mod 8),则(*)无整数解.
对于D≡2(mod 4)的情形,即Pell方程(*)变为
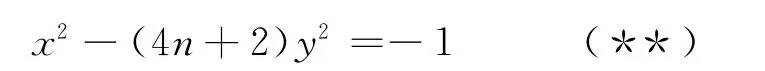
则比较复杂.本文就Pell方程(**)的解进行讨论.
1 预备知识
引理1[6]当n∈Z+时,一切大于2的质数,不是形如4n+1就是形如4n-1.
引理2[6]当n∈Z+时,任意多个形如4n+1的数的积仍是4n+1的数.
2 相关定理及证明
2.1 n为奇数的情形
定理1 当n为奇数且2n+1为素数时,(**)无整数解.
证明 当n为奇数时,令n=2k+1(k∈N),因为2n+1为合数,所以4k+3为合数.设4k+3=pi(pi为质数,i=1,2,…,s),则由引理1,得pi(i=1,2,…,s)不是形如4n+1就是形如4n-1的数.若pi(i=1,2,…,s)全为4n+1型,则由引理2,得pi仍是4n+1型的数,这与“4k+3(=4(k+1)-1)是4n-1型的数”矛盾,故pi(i=1,2,…,s)中至少有一个是4n-1(=4(n-1)+3)型的数,即4k+3中至少有一个是4m+3型的素因数.因此,由定理3′,得式(1)无整数解,故(**)无整数解.则(**)为x2-(8k+6)y2=-1,即
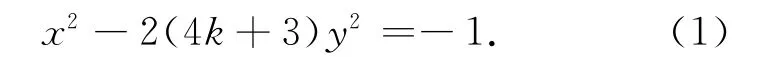
因为2n+1为素数,所以4k+3为素数.由定理3′得,式(1)无整数解,故(**)无整数解.
定理2 当n为奇数且2n+1为合数时,(**)无整数解.
证明 当n为奇数时,令n=2k+1(k∈N),则(**)为x2-(8k+6)y2=-1,即
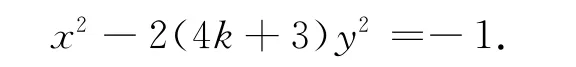
2.2 n为偶数的情形
证明 当n为偶数时,令n=2k(k∈N),则(**)为x2-(8k+2)y2=-1,即
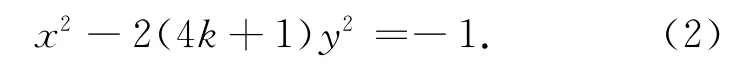
定理4 当n为偶数且2n+1中含有4m+3型素因子时,(**)无整数解.
证明 当n为偶数时,令n=2k(k∈N),则(**)为x2-(8k+2)y2=-1,即
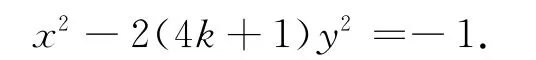
由于2n+1中含有4m+3型素因子,则8k+2中含有4m+3型素因子.因此,由定理3′,得式(2)无整数解,故(**)无整数解.

因为k为单数,设k=2k′+1(k′∈N),则2n+1=4k+1=8k′+5,所以8k′+5≡5(mod 8),即2n+1≡5(mod 8).又因为2n+1为素数,故由定理2′,得式(2)有正整数解,所以(**)有正整数解.
3 实 例
例 判断下列方程是否有解:
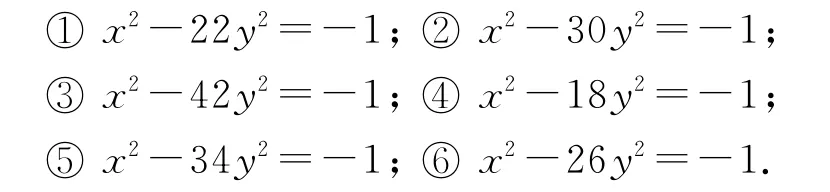
解 ① 因为22=2×11=2×(2×5+1),5为奇数,故由定理1,得x2-22y2=-1无整数解.
② 因为30=2×15=2×(2×7+1),7为奇数且15=3×5,故15中含素因数3和5,故由定理2,得x2-30y2=-1无整数解.
③ 因 为42=2×21=2×(2×10+1),10为偶数且,故由定理3,得x2-42y2=-1无整数解.
④ 因 为18=2×9=2×(2×4+1),4为偶数且9中含素因数3,故由定理4,得x2-18y2=-1无整数解.
⑤ 因 为34=2×17=2×(2×8+1),8为偶数且34=32+52,3≡3(mod 8),5≡-3(mod 8),故由定理5,得x2-34y2=-1无整数解.
[1] 赵丕卿,赵刚堂.Pell方程x2-(a2-1)y2=k的解集[J].沈阳大学学报,2009,21(5):107-110.
[2] 杜先存,万飞,赵金娥.Pell方程ax2-by2=1的最小解[J].湖北民族学院学报,2012,30(1):35-38.
[3] 柯召,孙琦.谈谈不定方程[M].哈尔滨:哈尔滨工业大学出版社,2011:22-23.
[4] 曹珍富.不定方程及其应用[M].上海:上海交通大学出版社,2007:2-4.
[5] 曹珍富.丢番图方程引论[M].哈尔滨:哈尔滨工业大学出版社,1989:160-161.
[6] 王进明.初等数论[M].北京:人民教育出版社,2002:27.
