框架域子带间局部隐马尔可夫模型在图像去噪中的应用

申 森

（太原大学外语师范学院，山西 太原 030012）

框架域子带间局部隐马尔可夫模型在图像去噪中的应用

申 森

（太原大学外语师范学院，山西 太原 030012）

噪声是影响图象质量的主要因素，因此，有必要在分析和利用图像之前消除噪声。在本文中，研究了基于框架域子带间局部隐马尔可夫模型。这种模型能很好地捕捉小波框架系数的“聚集”特性，也能捕捉方向间小波框架系数的相关性。本文利用这种模型进行图像去噪。实验表明，本文提出的去噪方法取得了较高的去噪结果。

局部隐马尔可夫模型；图像去噪；小波变换

1.引言

图像在采集、获取以及传输的过程中，往往要受到噪声的污染，成为影响视觉质量的含噪图像。图像降噪的目的就是尽可能好地改善图像的质量。人们根据实际图像的特点、噪声的统计特征和频谱分布规律发展了各式各样的降噪方法，其中最为直观的方法是根据噪声能量一般集中于高频，而图像频谱则分布于一个有限区间的特点，采用低通滤波的方式进行降噪，例如滑动平均窗滤波器、Wiener 线性滤波器等。文献[1]通过建立描述边缘的数学模型，提出了边缘重构技术。Yang[2]，Charbonnier[3]提出了半二次正则化方法，能很好地保持图像的边缘。

近年来，人们将小波变换与其它方法结合实现对图像降噪。Crouse 等人将小波理论与马尔可夫模型(HMM) 联系起来，提出小波域隐马尔可夫模型[4]-[6]。一些学者利用小波域隐马尔可夫模型，特别是小波域隐马尔可夫树模型，来进行图像处理，如图像去噪[7][8]，图像分隔[9]。

2.基于框架域子带间局部隐马尔可夫模型

图像可以看作为二维矩阵，设图像为{f[i,j],i,j=1, 2,...,N}，其中 N =2s,s ∈Z+。二维框架变换可以将图像的基本特征在时域与频域中同时展现出来。设小波框架滤波器的低通滤波器为L，高通滤波器分别为H1,H2，则通过小波框架变换，图像变为九个子带：子带k=1,2,...,J 称为分辨率细节信息，其中J为最大分解尺度。子带LLJ称为最低分辨率低频信息。

图像经小波框架变换后小波框架系数呈现稀疏性分布，即大部分小波框架系数的幅值比较小，只有少部分小波框架系数幅值较大。实际上，小波框架系数的概率密度函数呈现尖峰值、重拖尾的非高斯分布特征。高斯混合模型可以很好地描述这种非高斯性。高斯混合模型描述如下：

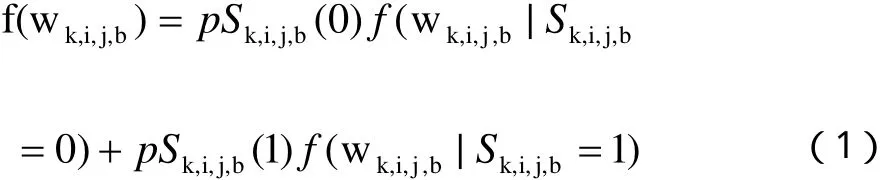
其中：

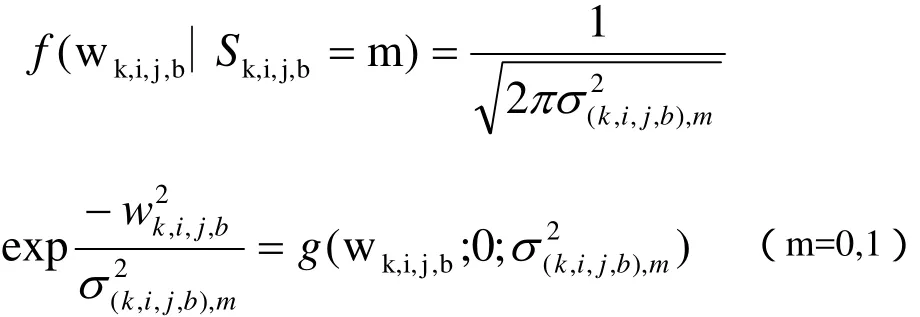
pSk,i,j,b(m)为 概 率 质 量 函 数 。 有 pSk,i,j,b(0)表示不同状态：表示小波框架系数处于状态 0 时的条件密度函数，表示小波框架系数处于状态1时的条件密度函数。

小波框架系数的幅值和它相邻的系数幅值有关，因此我们提出局部高斯混合模型，假设每个框架小波系数 wk,i,j,b符合局部高斯混合模型，其参数通过下式给出：

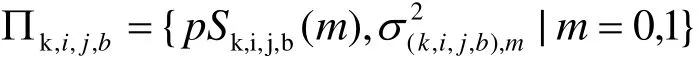
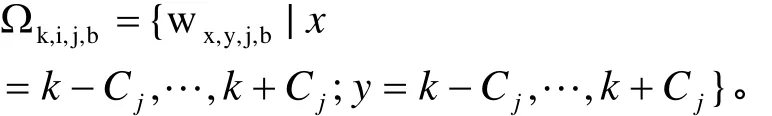
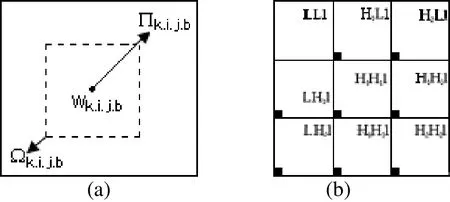
图1 ：(a) 局部高斯混合模型结构示意图。 (b) 局部高斯混合模型上的元素集合.黑点表示在同一尺度和位置的随机变量W。

子带之间的相关性对框架域是非常有用的。 为分析相关性，我们把在同一尺度和位置上的小波框架系数用wk,i,j=｛ wk,i,j,｜bb ∈B}表示，如图1.b所示，其中B={H1L ，我们通过定义随机变量如果则它的值为或者，如果则它的值为其中为集合的平均能量。利用高斯混合模型，把wk,i,j与式(1)结合,我们提出基于框架域的子带间局部隐马尔可夫模型。如下：

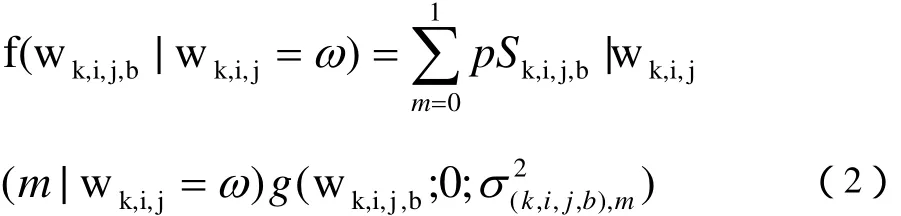
其中：

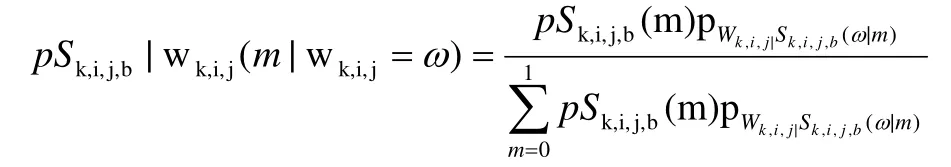
基于框架域的两状态，零均值子带间局部隐马尔可夫模型参数向量为：

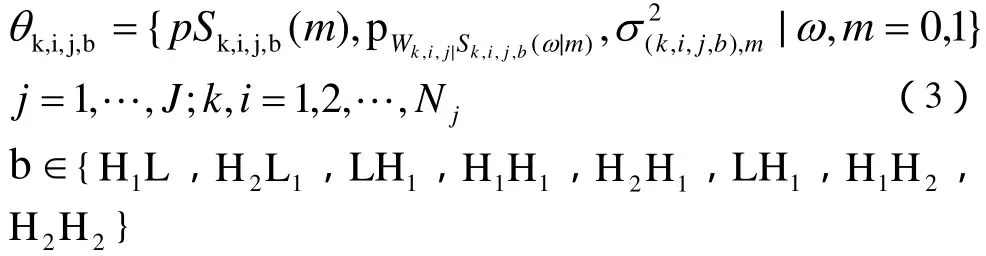
3.去噪算法和实验结果

数字图像去噪的模型如下：

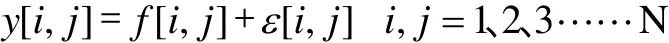
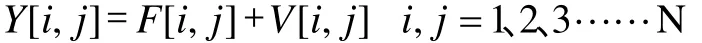
如F[i,j]服从零均值的混合高斯分布，则Y[i,j]也服从零均值的混合高斯分布，其方差为F[i,j]与噪声V[i,j]的方差之和，而其它参数与F[i,j]的参数相同。 因此，如果带噪图像Y[i,j]的参数为则原始图像 F[i,j]的参数为其中

给定子带间局部隐马尔可夫模型的参数, 可得F[i,j]的条件均值估计

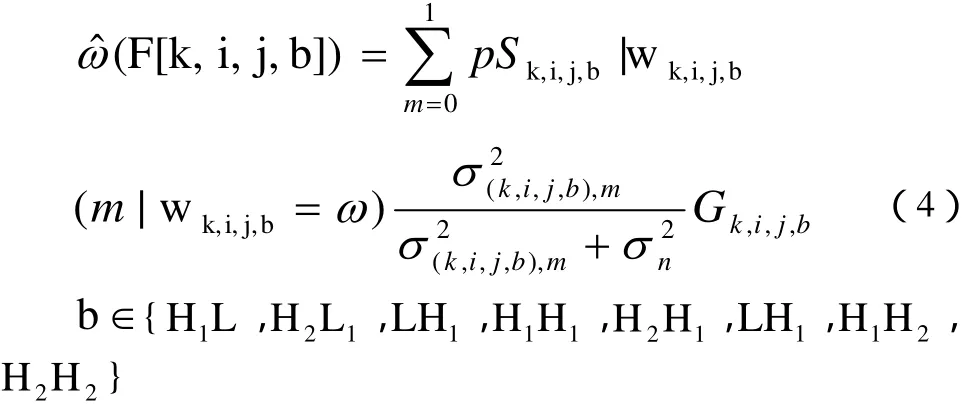
1）对观察到的图像 y[ i,j]进行J层小波框架分解。

2）通过 EM 算法估计基于框架域的子带间局部隐马尔可夫模型的参数向量。

3）对每一子带（最低频LL保持不变），通过（4）估计F [i,j ]。

4）对 F [i,j]进行逆小波框架变换，得到去噪图像fˆ[i,j]。

本文选取了lena图像进行去噪实验。给lena图像加零均值的标准高斯噪声，σ ∈｛10 ,15,20,25,30｝。去噪效果用峰值信噪比来衡量。

算法流程如下：

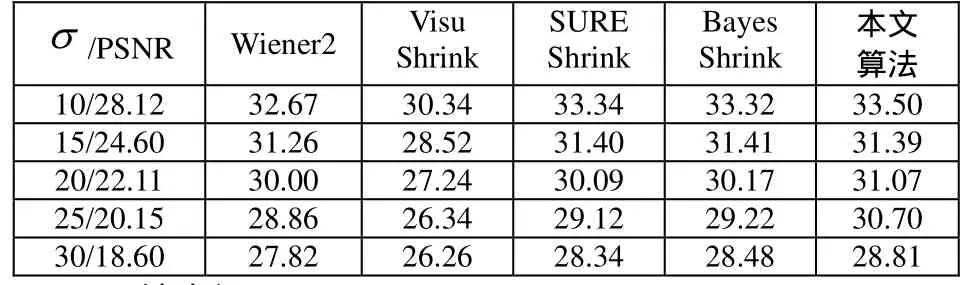
表1 不同算法的去噪比较(PSNR值)

4.结束语

在本文中，提出了基于框架域子带间局部隐马尔可夫模型。这种模型能很好地捕捉小波框架系数的“聚集”特性，也能捕捉方向间小波框架系数的相关性。本文利用这种模型进行图像的去噪处理。实验仿真表明，本文提出的去噪方法取得了较高的峰值信噪比。

[1] Guoliang Fan, Wai-Kuen Cham.Model-based reconstruction for low bit-rate wavelet-compressed images[J].IEEE,Transactions on Circuits and Systems for Video Technology,2000,V10(1): 120-132。

[2] D.Geman and C.Yang.Nonlinear image recovery with half-quadratic regularization and FFT’s [J].IEEE, Trans.Image processing, 1995,V(4)7:932-946。

[3] Pierre Charbonnier, L.Blanc-Feraud, G.Aubert, and Michel Barlaud.Deterministic edge-preserving regularization in computed imaging [J].IEEE, Trans.Image processing, 1997,V(6)2:298-311。

[4] Crouse M.S., Nowak R.D., Baraniuk R.G.Hidden Markov models for wavelet-based signal processing[C].In: Proceedings of the 30st Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 1996, 1029-1035。

[5] M.Crouse, R.Nowak, and R.Baraniuk.Wavelet-based statistical signal processing using hidden Markov models [J].IEEE Trans.Signal Process, 1998, V(46)4:886-902。

[6] M.Crouse, R.Nowak, and R.Baraniuk.Contextual hidden Markov models for wavelet-domain signal processing[A].Processing of the 31st Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 1997:95-100。

[7] J.Romberg, H.Choi, and R.Baraniuk.Bayesain tree-structured image modeling using wavelet domain hidden Markov Models[J].IEEE Trans.Image Process, 2001,V(10)7:1056-1068

[8] G.Fan and X.-G.Xia.Image denoising using local contextual hidden Markov model in the wavelet domain[J].IEEE Signal Process.Lett, 2001, V(8)5:125-128。

[9] H, Choi and R.Baraniuk.Multiscale image segmentation using wavelet-domain hidden Markov models[J].IEEE, Trans.Image Processing, 2001, V(10):1309-1321。

TN941.2+1

A

1008-7427（2012）04-0159-02

2012-02-24