一种基于粗糙集理论的灰度图像增强方法

张 艳， 阳 博

(中南林业科技大学 计算机与信息工程学院，湖南 长沙 410004)

0 引言

在自然科学、社会科学与工程技术的很多领域中，都不同程度地涉及到对不确定因素和不完备信息的处理。1965年Zadeh创立的模糊集理论与1982年Z.Pawlak倡导的粗糙集理论是处理不确定性的两种很好的方法。除了之外，基于概率统计的方法也是处理不确定性的一种有效方法。与模糊集和概率论等方法相比，粗糙集方法的最大优点是不需要附加信息或先验知识，在模糊集方法与概率统计等方法中，往往需要模糊隶属函数、基本概率指派函数和有关统计概率分布等，而这些信息有时并不容易得到。正是基于这一优点，粗糙集理论得以迅速兴起，并逐渐成为人工智能以及其他处理不确定性领域的研究热点，广泛应用于在机器学习，知识获取，数据挖掘，决策分析，过程控制，模式识别等领域[1-3]。

在灰度数字图像的增强处理中,作为一种和模糊集理论不同的方法，粗糙集理论将图像看成一个知识系统，基于不可分辨关系，根据像素的两个条件属性：灰度值属性和噪声属性，将像素分类到不同等价类，即划分成明暗区域和噪声区域，利用粗糙集的上下近似原理，求得无噪声区的粗糙集表示方式，并对较亮无噪声子图，采用直方图均衡变换，对较暗无噪声子图，采用指数变换，最后重叠，从而达到增强非边缘区域，减弱噪声的目的。

1 粗糙集基本原理

1.1 几个基本概念

论域U：由研究对象组成有限非空集合，记为U，称为论域。

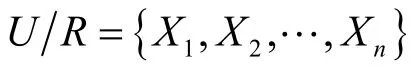
不可分辨关系IND( P)：在U上某个等价关系簇中的全部等价关系的交集，称为不可分辨关系，不可分辨关系也是等价关系[4]。

1.2 粗糙集和上下近似

令X是U的子集，R是U上的一个等价关系，若X可以用R中的某些等价类求并得来，则X是精确集，否则X是粗糙集。作为粗糙集X，可用其两个精确集来描述：上近似和下近似[5]。

1)下近似R_(X)：X的一个最大子集，其中的元素肯定是R下U中所有能归入X的元素。

2)上近似R_(X)：包含X的一个最小集合，其中的元素是在R下U中可能归入X的元素。

3)边界域=上近似—下近似，即BNR(X)=R_(X)-R_(X )，边界域中的元素既不能肯定归于X，也不能肯定归入-X。当R_(X)=R(X )时，集合 X关于R是精确集，而_R_(X)≠R_(X)时，X关于R是粗糙集，可用(R_(X),R_(X))这对集合来近似表示。

应用粗糙集来判断分类，是根据某些条件属性判断决策属性的分类。比如在灰度图像中，某些像素点的灰度值大于一定阀值，则仅根据灰度值这一属性可以判断这些点属于“较亮”的集合。在这个集合中，这些点是不相互区别的。而若再加上与相邻子块的灰度值之差(即噪声)这一属性，则这些原本确定属于“较亮”集合的点，则可能属于“较亮边缘噪声”集合了。这一可能性就反应了粗糙集所研究的不确定性，可用来处理模糊不确定的边缘特性[6-8]。

2 基于粗糙集的灰度图像增强方法

将一幅大小为M×N的二维图像作为U，像素点x为U中的一个对象，f( x, y)为x的灰度值。

2.1 像素点分类

定义灰度图像的两个条件属性c1和c2，c1表示像素点灰度值属性，c2表示两相邻子块的平均灰度值之差的绝对值，即噪声属性，记C={c1，c2}。而决策属性d表示像素的分类，为方便表示，d= {1,2,3,4}，1表示较亮无噪声区，2表示亮区的边缘噪声区，3表示较暗无噪声区，4表示暗区边缘噪声区。

利用不可分辨关系的概念，将U中的像素点分别按两个条件属性划分等价类，划分方法具体如下：

1)对于c1灰度值属性，某个像素点 x的灰度值fc1(x, y)，若 fc1(x, y)满足：

Rc1={(x, y)|fc1(x, y)＞f1}，f1为灰度值阀值，则c1=1，表示该像素点的灰度值在[f1+1,255]之间，归入Rc1等价类，表示该像素点属于图像中的“较亮”的集合。否则c1=0，表示像素点的灰度值 fc1(x, y)在[0,f1]之间，归入Rc1的非集等价类，表示该像素点属于图像中的“较暗”的集合。

2)对于c2噪声属性，将图像可按1×1，2×2或4×4像素组成子块进行分块，对子块与相邻子块的像素灰度平均值之差的绝对值，记为fc2(x, y) =int|m( Sij)-m( Si±1,j±1)|，若fc2(x, y)满足：Rc2={(x, y)|fc2(x, y) ＞f2}，f2为噪声阀值，则c2=1，表示像素点x有噪声，归入Rc2等价类，即该像素属于边缘噪声集合。否则c2=0，表示像素点x无噪声，归入等价类，即该像素属于无噪声集合。

2.2 增强处理算法

根据粗糙集理论，对所有像素点xi，按照两个条件属性，判断其所属的集合，作为决策依据，对不同集合做出不同的增强处理，算法如下：

1)预处理：设原图像为X，求其直方图和大小，设定灰度阀值 f1和噪声阀值 f2。

2)取得较亮子图P，并做处理：对属于较亮集合的所有像素点灰度值用灰度阀值f1代替；对属于较亮区域边缘的噪声集合中的像素点灰度值用相邻子块灰度平均值代替。

3)取得较暗子图Q，并做处理：对属于较暗集合的所有像素点灰度值用灰度阀值f1代替；对属于较暗区域边缘的噪声集合中的像素点灰度值用相邻子块灰度平均值代替。

4)分别采取不同的变换：对较亮子图P作直方图均衡变换，使较亮区域变得更清晰；而对较暗子图Q作直方图指数变换，系数取值越大则亮区范围越扩大，以增强较低灰度级别的细节。

5)输出：将两个子图重叠后，输出最终的增强图像。

2.3 阀值选取

对灰度图像来说，直方图有几种情况：

1)若直方图只有明显的两个峰值，一个峰值代表较亮区域灰度值，一个峰值代表较暗区域灰度值，那么就简单地取两峰中间所对应的灰度值为灰度阀值 f1，噪声阀值 f2取 f1的一半。如文中使用的图像2.bmp。

2)若直方图中峰值有多个，则需要用其他方法计算灰度阀值，如用遗传算法计算最大类间方差阀值等方法得到 f1，f2=f1/2。如文中使用的图像1.bmp。

3)若原图分辨率很低，有较大噪声，直方图分布很稀，则取较密集分布的峰值的中间值为灰度阀值f1，f2=f1/2。如文中使用的图像3.bmp。

3 实验结果与分析

现针对2.3节描述的直方图的3种情况，选取了3幅二维灰度图像，分别实验了上面阐述的增强方法，子块按1×1的像素进行划分，得到的增强效果如图1﹑图2﹑图3﹑图4﹑图5和图6所示，在明暗区域细节上均有明显增强：

图1 原始图像1.bmp

图2 增强图像12.bmp

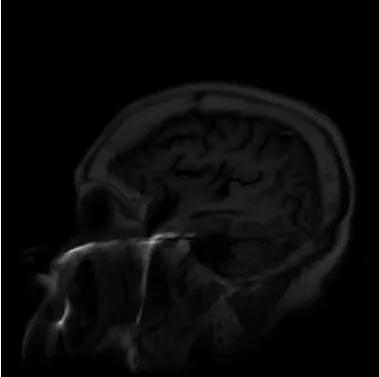
图3 原始图像2.bmp

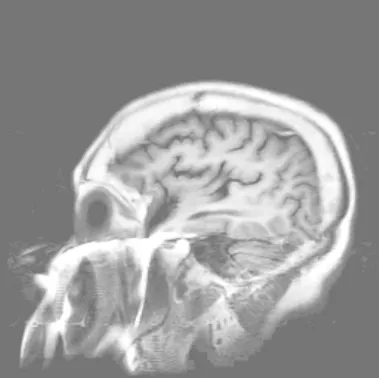
图4 增强图像22.bmp

图5 原始图像3.bmp

图6 增强图像32.bmp

1)图像1大小为512×512，灰度阀值 f1=180，f2=90，指数变换系数c=3.8。

2)图像 2大小为 256×256，灰度阀值 f1=40，f2=25，指数变换系数c=7.6。

3)图像 3大小为 364×239，灰度阀值 f1=30，f2=15，指数变换系数c=6.5。

4 结语

二维灰度图像，有明显较亮和较暗区域，而边缘区域的噪声往往影响图像的质量[9-10]，为了增强图像的对比度，对低灰度级别有丰富细节进行增强。文中的实验初步尝试并比较了 3种不同直方图特性的图像在采用该方法后得到的效果，可以看出在明暗增强及边缘噪声处理效果和对低灰度级别有丰富细节的图像有增强效果。文中阐述了灰度图像增强的一种方法，针对不同特性的直方图还可研究阀值选取的其他方法，并进一步研究粗糙集与其他增强算法结合的方法，更好地提高图像质量。

[1]高会生,冯力娜.基于粗糙集的电力通信网综合权重确定方法[J].通信技术，2009,42(10):145-147.

[2]唐忠,曹俊月.基于粗糙集属性约简的 SVM异常入侵检测方法[J].通信技术，2009,42(02):261-263.

[3]郑梦泽.基于粗糙集的交通信号控制决策研究[J].通信技术，2010，43(04):225-226.

[4]胡寿松,何亚群.粗糙决策理论与应用[M].北京: 北京航空航天大学出版社，2004.

[5]张文修,吴伟志.粗糙集理论介绍和研究综述[J].模糊系统与数学，2000,14(04):1-12.

[6]徐立中,王慧斌,杨锦堂.基于粗糙集理论的图像增强方法[J].仪器仪表学报,2000,21(05):514,524.

[7]刘映杰,马义德,夏春水.粗糙集理论及其在图像处理中的应用[J].计算机应用研究，2007(04):176-178.

[8]李孟歆,吴成东,侯静.粗糙集在图像处理中的研究进展[J].仪器仪表学报，2008(08):230-233.

[9]唐崇武,李会方,何俊婷,等.改进的直方图均衡图像增强算法及实现[J].信息安全与通信保密，2009(12):72-75.

[10]李侃.粗糙集文本过滤系统研究及硬件实现[J].信息安全与通信保密，2006(03):44-46.