较为精密的Hardy-Hilbert不等式的一个加强
2012-10-26隆建军
隆建军
较为精密的Hardy-Hilbert不等式的一个加强
隆建军
(攀枝花市大河中学,四川,攀枝花 617061)

Hardy-Hilbet不等式;权系数;Euler-Maclaurin不等式
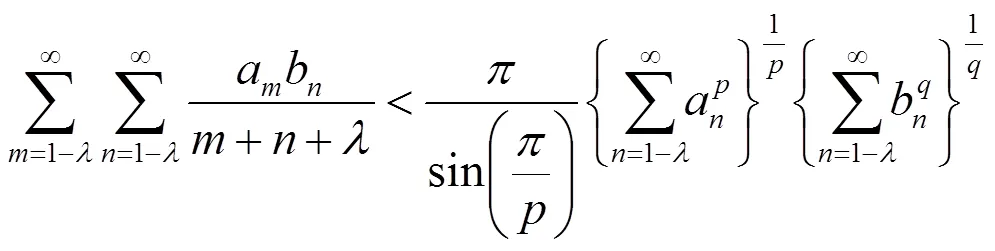

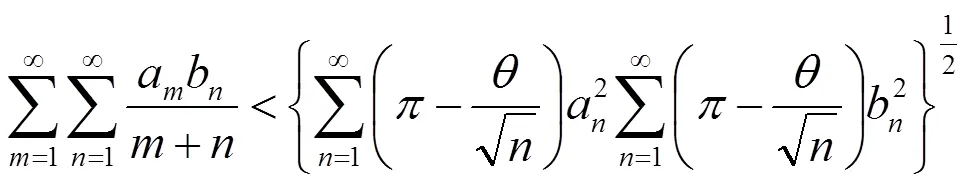
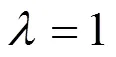
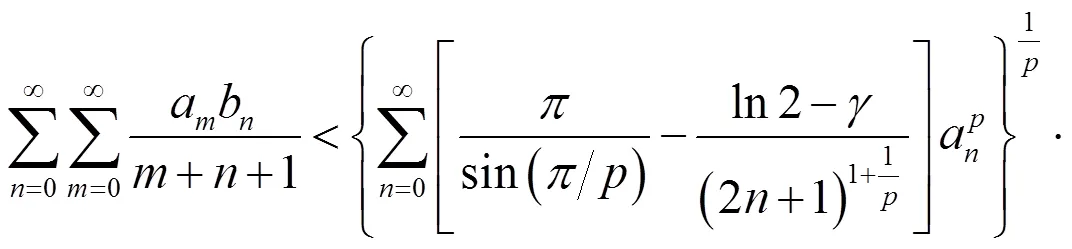

2003年,Bicheng Yang建立如下权系数不等式[9]:
得到(1)的一个改进形式:
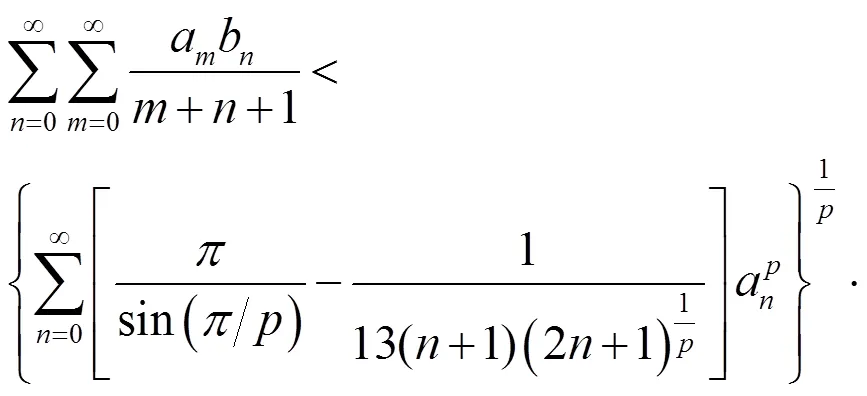



1 几个引理
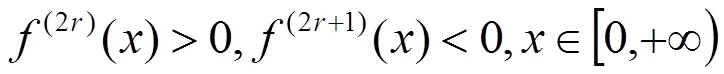



所以,由Euler-Maclaurin求和公式公式和以上计算,有



又由于

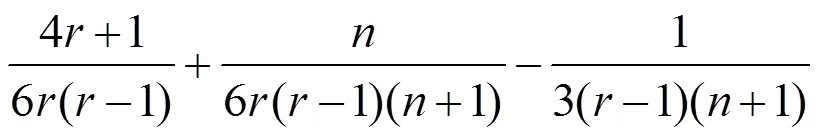

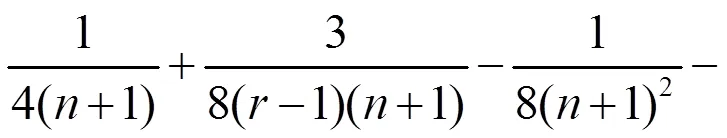
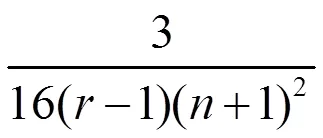

把(9)、(10)、(11)式代入(8)式,有
即
所以有
故,引理2的(7)式成立。
2 主要结论及其证明
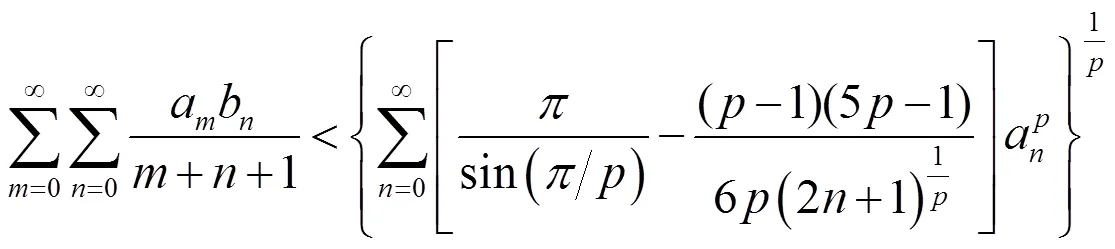




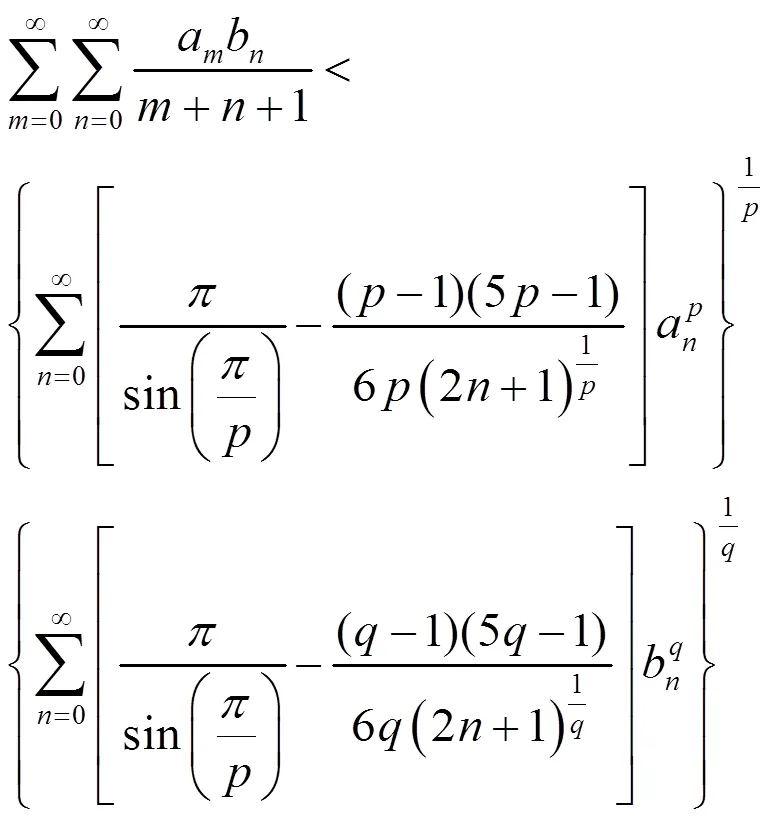
故定理1的(12)式成立。证毕。

由(7)式和以上所得,有
故定理2成立。证毕。
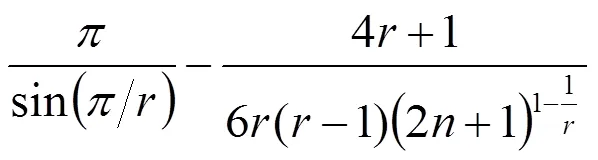
[1] Hardy G H, Littlewood J E, Polya G. Inequalities[M]. Cambridge: Cambridge Univ Press,1952.
[2] 高明哲.关于Hilbert重级数定理的一个注记[J].湖南数学年刊,1992,11(1-2):142-147.
[3] 赵德钧.关于Hilbert重级数定理的一个改进[J].数学的实践与认识,1993(1):85-90.
[4] 杨必成.关于一般Hilbert重级数定理的改进[J].数学研究,1996,29(2):64-70.
[5] 杨必成,高明哲.关于hardy-Hilbert不等式的一个最佳常数[J].数学进展,1997,26(2):159-164.
[6] 杨必成,朱匀华.正实轴上的Hurwitz ζ-函数不等式[J].中山大学学报,1997,36(3):30-25.
[7] Hsu L C,Wang Y J.A refinement of Hilbert's double series theorem[J].J Math Res Exp,1991,11(1):143-144.
[8] Yang B.On a strengthened version of the more accurate Hardy-Hilbert's inequality[J].Acta Math.Sinica(N.S.), 1999, 42:1103-1110.
[9] Yang Bicheng. A strengthened Hardy-Hilbert's inequality[J]. Proceedings of the Jangjeon Mathematical Society, 2003, 6(2):119-124.
[10] 徐立治,王兴华.数学分析的方法及例题选讲[M].北京:高等教育出版社,1985:81-98.
ON A STRENGTHENED VERSION OF THE MORE ACCURATE HARDY-HILBERT'S INEQUALITY
LONG Jian-jun, YANG Hou-xue
(Dahe Middle School of Panzhihua, Panzhihua, Sichuan 617061,China;)

Hardy-Hilbert inequality; weight coefficient; Euler-Maclaurin inequality
O178
A
10.3969/j.issn.1674-8085.2012.04.006
1674-8085(2012)04-0025-05
2012-01-07;
2012-03-21
隆建军(1981-),男,四川安岳人,中学二级教师,主要从事解析不等式研究(E-mail: longjianjun1234@163.com).
