加工时间不确定的船体分段空间调度方法

张志英，张风薇

(同济大学 机械工程学院，上海200092)

目前在大型离散制造企业如船舶和飞机制造中，动态空间调度是一个典型问题，它是指在空间布局的基础上兼顾时间效率，综合考虑空间因素和时间因素相互制约、相互影响的耦合关系，从而来安排生产调度计划.针对这类问题，目前专家学者普遍采用的解决方法是人工智能优化算法和基于规则的启发式方法［1］.

针对船舶建造过程中的空间调度问题，Lee等提出了基于船舶形状的启发式调度规则［2］;郑俊丽等运用形状相似和工艺相似策略，提出了一种缩短最大完工时间的船舶分段空间调度算法［3］;陈洁等运用运筹学方法结合场地平均时空利用率指标构建综合加工优先顺序、交货期等因素的非线性规划模型［4］.然而，上述方法都将船舶分段空间调度假定为在一个确定的生产环境中进行，实际船舶分段建造过程中往往存在大量不确定因素如急件插入和随机的设备故障等，而且还存在大量不精确信息如分段开工时间、完工时间和加工时间等，以及不完备信息如原材料的质量状况、在制品生产情况等.这些不确定因素、不精确和不完备信息会导致分段及其关联件的建造不能按照计划进行，出现提前/拖期等现象，最直接体现在对加工时间的影响，使得加工时间表现为模糊数［5］或随机分布，如正态分布［6］.因此，这种由随机环境产生的调度方案也不是唯一的，根据计划人员对生产环境给出的不同评估，在不同影响因子条件下将有不同的调度方案.这就需要研究不确定环境下的调度问题，针对各种置信水平的不确定生产环境提出可行的调度解.张丽华等在加工时间和工件交付期都服从指数分布的条件下，提出了最优调度的几个性质，并运用动态规划的方法给出了求解最优解的算法［7］;朱海平等提出一种支持多目标和多优先级车间调度策略的随机规划模型，并给出了求解算法，从而在不确定的车间信息环境下做出正确调度策略［8］;R.Tavakkoli-Moghaddam等提出了解决设备布局问题的数学模型，运用该模型能最小化设备、厂房布局的总成本［9］.

本文综合考虑了分段空间调度问题中的时空耦合性以及不确定因素造成的加工时间随机性，建立加工时间不确定环境下的船体分段空间调度模型，结合某大型船厂实际生产数据进行验证，得出不同置信水平下的调度解，结果表明该方法更符合船厂分段建造调度的实际情况.

1 问题描述与假设

在船舶分段建造中，空间调度问题普遍存在.与以往生产知识确定下的分段调度相比，该类问题主要体现在分段建造的时间还受到其关联件的影响，并且加工时间不再是唯一确定的，而是服从随机分布的变量.而一般的船体分段建造空间调度问题可以简化为分段最大包络投影面积以及时间因素的三维装箱模型，在时间约束方面，若分段之间具有紧前紧后关系，那么后续分段只有在前面的分段生产完毕后才能开始生产，而如果分段带有旁板等关联件的，分段和旁板的加工时间必须满足它们的关联约束.在空间方面，分段和分段之间不允许出现干涉现象，分段放置也不允许超出场地边界.若假设场地和分段的投影都为矩形，则分段建造空间调度模型如图1所示.

图1 包含5 个分段 B={B1，B2，B3，B4，B5}，其中 P1、P2分别是 B1、B2的旁板，受 B1、B2的关联约束作用.当旁板P2在建造过程中遇到不确定因素，加工时间延长同时直接影响到B2、B52个分段.由于P2的拖期使得B2的加工时间也相应地增加，此外B5拖期会超出整个场地的生产周期.在这种情况下，需要重新安排分段和旁板在场地上的位置，使得分段能按计划完工，减少因不确定因素额外产生的成本.而一般旁板开工时间和对应分段开工时间有关联约束，因此旁板的调整需考虑对应分段的时间和空间的安排，对于图1的模型，当产生上述不确定情况时，一种调整方法是将B5重新布局，如图2所示.

图1 分段空间调度模型Fig.1 Block spatial scheduling model

由图2可知，经过调整后的分段和旁板满足时间和空间约束，同时减少了因不确定因素对其他分段产生的影响，具有较高的生产效率.

在船体分段建造的诸多不确定因素中，加工时间不确定最常见，这里主要考虑因分段关联件旁板加工时间而引起分段加工时间的不确定性.因此，该类问题可描述为:在一个调度计划周期内有n个待调度的船体分段 B={B1，…Bi，…，Bn}，每个分段Bi对应有若干个旁板，总共有x个旁板(其中i代表分段编号，i≥1;x代表旁板总数，x≥0)，将所有旁板按最早开工时间排序得旁板集合P={P1，…，Pg，…，Px}，分段和旁板在m个场地上加工.

图2 调整后的调度结果Fig.2 The schedu ling result after adjust ment

在加工时间不确定的分段建造动态空间调度问题中需要满足以下约束:

1)待调度的分段和旁板抽象为其垂直投影的最小包络矩形，假设矩形只有0°和90°2种放置状态，令长边li/lg平行于x轴的状态为1，反之为0;

2)场地形状假设为矩形.场地k长度为Lk，宽度为Wk，设场地左下角为坐标原点(0，0)，建立以长度方向为x轴，宽度方向为y轴，竖直方向为时间z轴的三维坐标系(以上均为正方向);

3)一个分段和旁板不能同时在不同的加工平台上加工，且一旦开始加工，必须等到完成后才能移出;

4)由于分段和旁板的加工时间受不确定因素影响，在实际生产中体现为以计划给出的加工时间为均值，服从某种随机分布的变量.本文假定分段和旁板的实际开工时间、加工时间和完工时间都服从正态分布，而仅有最早开工时间和交货期为确定值;

5)假设人员充分，设备无故障，忽略分段和旁板的吊运时间和其他物料的准备时间，即认为仅有旁板加工过程中的不确定性能传递给与它相应的分段，并且这种不确定性能积累从而影响到分段建造的空间调度结果，最直观表现为分段和旁板的加工时间为服从正态分布的随机变量.

在满足上述约束条件下，由于生产环境不确定因素影响造成分段建造的提前和拖期，提前完工产生存储成本，拖期完工产生延迟成本.本文以旁板建造加工时间的偏差作为整体分段建造调度过程中唯一不确定影响因素，建立加工时间不确定条件下的分段建造空间调度模型.为了描述这个模型，这里引入时空占用成本(time-space occupied costs，TSOC)指标.

由于分段建造提前完工和拖期完工产生的成本不一样，一般拖期完工比提前完工产生的成本要大很多，而不同分段由于尺寸差异，占用的空间成本也不同.本文以分段和旁板的最大包络投影面积和实际完工时间对交货期的偏差量乘积为时空占用成本，有以下相关定义:

定义1 对长为l，宽为w的分段，若完工时间c早于交货期d，则它的提前时空占用成本:

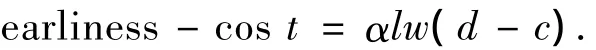
其中α是分段的提前完工惩罚成本.

定义2 对长为l，宽为w的分段，若完工时间c晚于交货期d，则它的拖期时空占用成本:

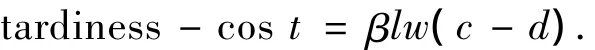
其中β是分段的拖期完工惩罚成本.

定义3 对带关联约束的分段，还有旁板加工时间偏差累积产生的偏差时空占用成本:

其中，|var(p)|表示分段加工时间p受不确定因素影响的偏差值，ξp表示概率P条件下，服从标准正态分布的变量.

对于选定生产周期内的分段和旁板总的时空占用成本，由于它既包含提前时空占用成本和拖期时空占用成本，还有旁板加工时间偏差累积产生的偏差时空占用成本，因此总的时空占用成本为这三部分成本的累加和.

定义4 对于选定生产周期内的分段和旁板总的时空占用成本:

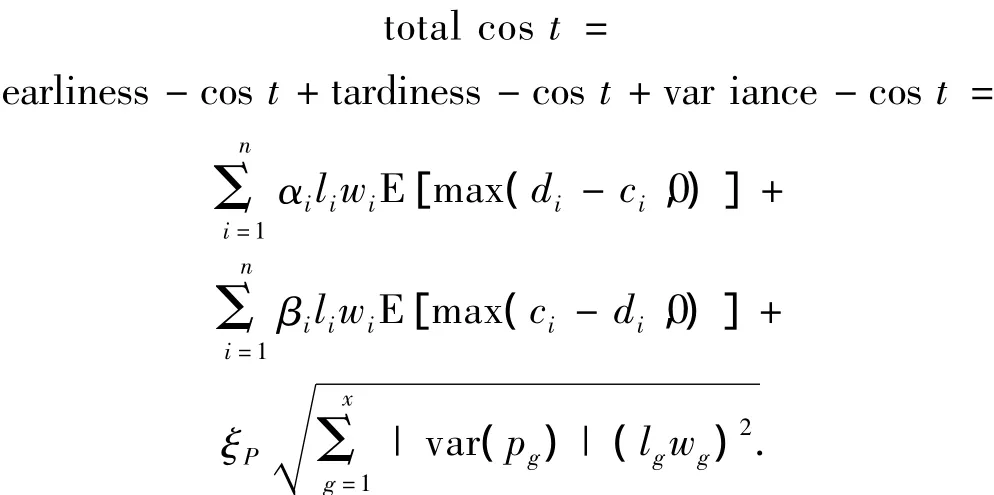
针对加工时间不确定的分段空间建造模型，它的目标是最小化TSOC，以得到不同置信水平下的调度解.根据以上假设，含关联约束的加工时间不确定分段建造空间调度问题解可表示为

其中:η为根据实际生产情况选择的置信水平;i、g表示分段号和旁板号;xi、yi表示分段i左下点坐标;xg、yg表示旁板g左下点坐标;zi表示分段i实际开工时间;zg表示旁板g实际开工时间;dxi/dxg表示分段i/旁板g相对于场地的放置方向，若长边li/lg平行于x轴，则dxi/dxg为1，反之为0;fi/fg表示分段i/旁板g经过计划后放置的场地.

2 不确定空间调度模型

2.1 机会约束下的不确定规划模型

分段空间调度问题通常用非线性规划模型来描述.而考虑不确定因素的调度问题，由于目标函数和约束条件已经不能按通常意义理解，因此要考虑有别于确定条件下调度模型的新理论和算法.机会约束规划就是这样一类符合不确定条件下含随机变量的新规划理论，其特点是随机约束条件至少以一定的置信水平成立.下面引入文献［16］给出的机会约束和不确定规划的概念.

假设x是一个决策向量，E是一个概率分布已知的随机向量，由x和E确定的n个目标函数记为fi=(x，e)，1 ≤ i≤ n，它受制于 m 个约束函数gj=(x，e)，1≤j≤m.由于目标函数和约束函数都具有随机性，因此只能通过置信概率的形式对目标和约束进行描述.因此，对应的机会约束可以表示为P{gj(x，E)≤0}≥α j，1≤j≤m，其中 P 表示随机事件gj(x，E)≤0发生的概率，αj为置信概率;若规划问题的目标是fi=(x，E)，1≤i≤n尽可能小，可取置信概率为βi，则任一目标函数表示为

基于多机会约束的多目标不确定性规划模型可表示为

2.2 不确定空间调度策略

在船舶分段建造过程中，分段在场地上的加工时间是服从某种分布的随机变量，因此分段的完工时间也是不确定的，分段建造空间调度约束可以描述为机会约束.假设有n种置信水平，则受关联约束的加工时间不确定分段建造空间调度模型将产生n个调度解，分别归为集合 S1，S2，…，Sn，每个集合对应的置信概率分别为 α1，α2，…，αn，令空间调度的空间和时间约束为

减少因提前、拖期产生的时空占用成本是调度的主要目标.设不同随机因素的影响下，置信概率分别为 η1，η2，…，ηr，用机会约束描述为

综合2.1和2.2节，受关联约束的加工时间不确定的分段建造空间调度问题在已知分段和旁板的尺寸、交货期，加工时间均值和偏差的情况下不确定规划模型为

根据以上理论和假设，对受关联约束的加工时间不确定的分段建造空间调度模型进行建模，详见2.3 节.

2.3 数学规划模型

空间调度非线性规划模型如下:

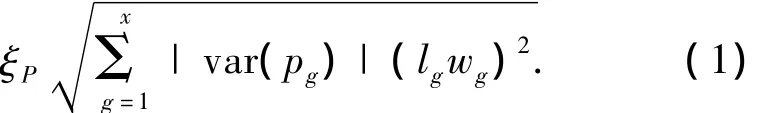
目标函数(1)表示在不同置信水平η(ξP)下，将旁板建造随机性对分段建造产生的影响最小化，同时所引起的分段建造提前、拖期成本也最小化.

约束(2)表示旁板最早开工时间和分段最早开工时间之间的关系.其中，ti、tg分别代表分段i旁板g的最早开工时间;a代表旁板上胎和分段上胎的时间关系.

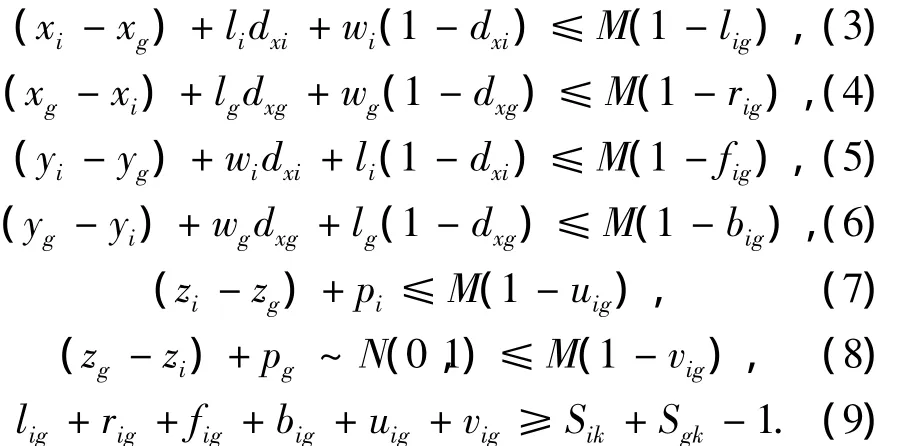
约束(3)～(9)表示同一场地内的分段和旁板的放置位置不允许重合.其中，xi、yi、zi代表分段 i的左下前坐标，xg、yg、zg代表旁板g的左下前坐标;lig、rig、fig、big、uig、vig、Sik、Sgk是决策变量，当分段 i在旁板g的左边时，lig等于1，否则为0;当分段i在旁板g的右边时，rig等于1，否则为0;当分段i在旁板g的前边时，fig等于1，否则为0;当分段 i在旁板g的后边时，big等于1，否则为0;当分段i比旁板g先加工时，uig等于1，否则为0;当分段i比旁板g后加工时，vig等于1，否则为0;当分段i/旁板g被安排在场地k上加工时，Sik/Sgk等于1，否则为0.

约束(10)～(16)表示同一场地内的分段和分段的位置放置不允许重合.

约束(17)～(23)表示同一场地内的旁板和旁板的位置不允许重合.

约束(24)和(25)表示加工过程中的分段和旁板位置唯一，只有等加工完毕后才允许从胎位移出.

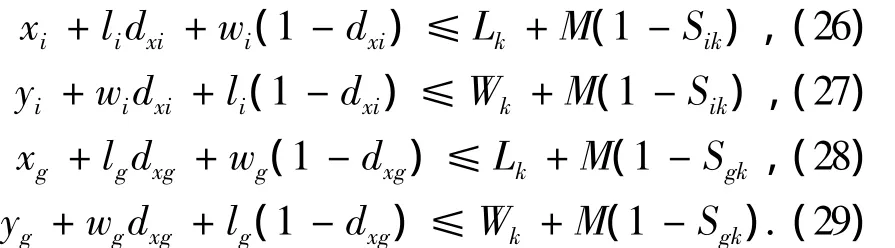
约束(26)～(29)表示待调度分段和旁板不能超过场地边界.

约束(30)和(31)表示待调度分段和旁板只能在所有前序工作提供完善生产资料的情况下才能开始加工.

约束(32)表示待调度分段和旁板的参考点坐标都为非负.该模型考虑旁板建造对分段建造的影响，将旁板加工时间进行随机处理，以分段建造提前或拖期产生的时空占用成本最小化为目标，对分段加工涉及的时间和空间因素给出调度结果.

3 实例验证与分析

3.1 实验例证

为了验证上述模型的正确性，本文以上海某大型船厂的分段和旁板建造空间调度数据为例，利用LINGO 11.0 软件，在处理器为 1.86 GHz，内存为1 GB的计算机上进行求解.实验包括以下输入参数:

1)待调度分段的数量、尺寸、最早加工时间、加工时间、交货时间、提前完工惩罚成本、拖期完工惩罚成本;

2)待调度旁板的数量、尺寸、最早加工时间、旁板上胎与分段上胎时间关系、旁板加工时间均值和偏差，其中偏差为计算机随机产生的符合标准正态分布的随机数;

3)场地数量和尺寸.具体输入数据见表1～3.

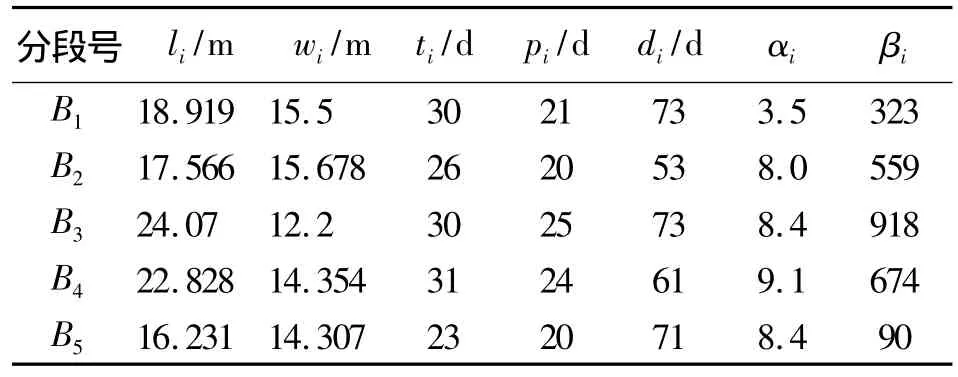
表1 待调度分段信息Table 1 Scheduling blocks information

表2 待调度旁板信息Table 2 Scheduling subsidiary parts information

表3 场地信息Table 3 Platform in formation m

通过不同置信水平对分段建造空间调度问题的求解，得到调度结果如表4所示，模型运行参数如表5.

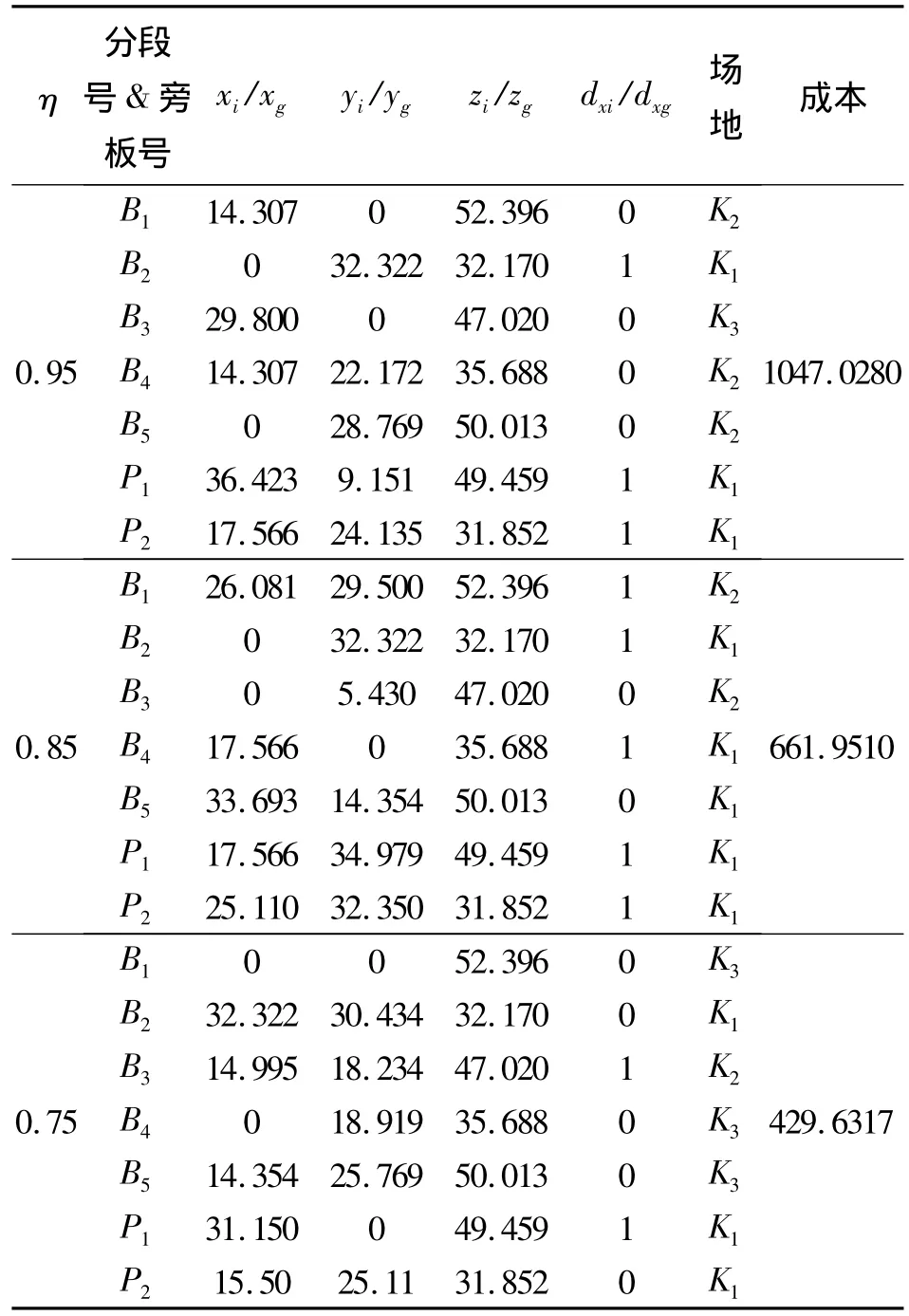
表4 实验验证结果Table 4 Experiment results

表5 部分模型运行参数Table 5 Part of model operation parameters

3.2 实验结果分析

以上实验结果给出了不确定环境下分段和旁板的具体加工信息.其中，置信水平越高，表示该种生产水平越接近确定条件下的生产环境.用该模型得到的可行调度方案是较优的，相对确定条件下的生产环境更接近船厂实际的生产情况.由于目标函数、变量和约束中都含有随机变量、随机约束，此外该模型涉及多场地的空间调度方法，因此这个模型的计算工作量相对较大，求解的模型规模不宜过大.从表4、5可以看出，当模型规模为5个分段和2个旁板时，模型求解时间在5 min左右，而模型求解时间和目标最优值与置信水平并没有严格的相关关系.如当置信水平为0.95时，CPU运行时间为00:04:02，分段提前、拖期时空占用成本为1 047.028 0;而当置信水平下降为0.85时，CPU运行时间减少为00:03:13，分段提前、拖期时空占用成本减少为661.951 0;当置信水平继续下降为0.75时，CPU运行时间又增加为00:08:06，分段提前、拖期时空占用成本减少为429.631 7.由此可见，加工时间不确定条件下的空间调度的时空占用成本并不唯一，它取决于不确定环境的置信水平.而空间调度问题在考虑了旁板对分段的关联约束后，问题变得更为复杂，需要考虑更多的约束，这样就大大增加了计算量.

3.3 确定条件下空间调度实验分析

确定条件下的空间调度问题是不确定条件下空间调度问题的一个特殊子问题.当置信水平为1，分段和旁板加工时间等于它们的均值，偏差为0时，随机空间调度问题就转化为确定性问题.由于不存在不确定因素造成的分段提前或拖期时空占用成本，目标函数改变为分段/旁板加工场地时空利用率最大化，如下

为比较2种情况下的空间调度问题，应用相同数据进行调度实验，调度结果见表6，模型运行参数见表7.

表6 确定条件下的实验验证结果Table 6 Experimental results in the certain environment

表7确定条件下部分模型运行参数Table 7 Part of model operation parameters in the certain environment

将表5和表7进行比较可以发现，当不确定问题转变为确定问题时，在变量数和约束数相同前提下，相同规模的空间调度问题的模型求解时间却大大减少.而由于问题的确定化，使得场地的利用率也大大提高，只需要在3号场地完成即可.因此，在不考虑不确定因素的前提下，该算法可以求解较大规模的模型，并且得到较优的仿真结果.而不确定因素由于将问题随机化，通常要结合机会约束和不确定规划等理论进行建模，主要解决的是不同置信水平下调度问题的求解，因此模型需要考虑开工时间、加工时间、完工时间等随机变量，此外还要考虑旁板对相关分段的关联约束，这就比确定条件下不具有关联关系的调度模型复杂得多，CPU运行时间就会大大增加.

4 结论

本文考虑了船厂生产过程中存在的不确定因素，提出针对不确定加工时间的分段建造空间调度非线性规划模型，重点分析因旁板生产中产生的提前、拖期因素导致的分段建造计划的偏离.旁板加工时间用正态分布随机数表达，而不同的置信水平将产生不同的随机偏差，这些偏差对对应分段的空间布局和加工时间产生影响.通过Lingo11.0对该非线性模型的求解，得出了不同置信水平下比较理想的调度解.由于该模型相对以往的研究加入了随机变量因素和关联件的时空影响，使得该模型更为复杂，也更接近于船厂的实际生产情况.

另一方面，该模型对于大规模空间调度问题很难进行求解.因此在今后的研究中，拟将问题规模缩小化或引入变量将非线性模型线性化，使得该模型也能适用于大规模的空间调度模型，此外在提高计算效率方面也有很多研究工作要深入开展.

［1］RYU C，SHIN JG，KWON O H，et al.Development of integrated and interactive spatial planning systems of assembly blocks in shipbuilding［J］.International Journal of Computer Integrated Manufacturing，2008，21(8):911-922.

［2］LEE JK，LEEK J，PARK H K，etal.Developing scheduling systems for Daewoo shipbuilding:DAS project［J］.European Journal of Operational Research，1997，97(2):380-395.

［3］郑俊丽，陈峰，江志斌，等.缩短最大完工时间的船舶分段空间调度算法［J］.上海交通大学学报，2009，43(4):663-668.ZHENG Junli，CHEN Feng，JIANG Zhibin，et al.A spatiotemporal scheduling algorithm minimizing make span［J］.Journal of Shanghai Jiao Tong University，2009，43(4):663-668.

［4］张志英，杨克开，于瑾维，等.改进粒子群算法的动态空间调度方法［J］.哈尔滨工程大学学报，2009，30(12):1344-1350.ZHANG Zhiying，YANG Kekai，YU Jinwei，etal.Dynamic spatial scheduling approach based on improved particle swarm optimization algorithm［J］.Journal of Harbin Engineering University，2009，30(12):1344-1350.

［5］张志英，陈洁.空间调度问题的非线性规划分析求解方法［J］.计算机集成制造系统，2010，16(6):1272-1277.ZHANG Zhiying，CHEN Jie.Nonlinear programming approach for spatial scheduling problem［J］.Computer Integrated Manufacturing Systems，2010，16(6):1272-1277.

［6］郭美娜，李波.基于树搜索的一种动态空间调度方法［J］.计算机工程与应用，2007，43(14):180-184.GUO Meina，LI Bo.Dynamic spatial scheduling approach based on tree-search［J］.Computer Engineering and Applications，2007，43(14):180-184.

［7］王蕾，张志英.基于规则的船体曲面分段空间调度方法［J］.上海交通大学学报，2009，43(11):1709-1714.WANG Lei，ZHANG Zhiying.Research on rule-based spatial scheduling in hull curved block construction［J］.Journal of Shanghai Jiao Tong University，2009，43(11):1709-1714.

［8］ENEA M，GALANTE G，PANASCIA E.The facility layout problem approached using a fuzzy model and a genetic search［J］.Journal of Intelligent Manufacturing，2005，16:303-316.

［9］GU Jinwei，GU Xingsheng，GU Manzhan.A novel parallel quantum genetic algorithm for stochastic job shop scheduling［J］.Journal of Mathematical Analysis and Applications，2009，355:63-81.

［10］张丽华，涂丰生.一个批处理机随机E/T调度问题研究［J］.系统工程理论与实践，2005，10:114-119.ZHANG Lihua，TU Fengsheng.An earliness and tardiness stochastic scheduling problem on a batch processor［J］.Systems Engineering——Theory ＆ Practice，2005，10:114-119.

［11］李素粉，朱云龙，尹朝万.具有随机加工时间和机器故障的流水车间调度［J］.计算机集成制造系统，2005，11(10):1425-1428.LISufen，ZHU Yunlong，YIN Chaowan.Flow shop scheduling with stochastic processing times and machine breakdowns［J］.Computer Integrated Manufacturing Systems，2005，11(10):1425-1428.

［12］朱海平，邵新宇，张国军.不确定信息条件下的车间调度策略研究［J］.计算机集成制造系统，2006，12(10):1637-1642.ZHU Haiping，SHAO Xinyu，ZHANG Guojun.Job-shop scheduling strategy under uncertain information environment［J］.Computer Integrated Manufacturing Systems，2006，12(10):1637-1642.

［13］TAVAKKOLI-MOGHADDAM R，JAVADIAN N，JAVADI B，et al.Design of a facility layout problem in cellular manufacturing systems with stochastic demands［J］.Applied Mathematics and Computation，2007，184:721-728.

［14］VÁZQUEZ-ROMÁN R，LEE Jinhan，JUNG Seungho，et al.Optimal facility layout under toxic release in process facilities:a stochastic approach［J］.Computer and Chemical Engineering，2010，34:122-133.

［15］YANG T，HUNG C C.Multiple-attribute decision making methods for plant layout design problem ［J］.Robotics and Computer-Integrated Manufacturing，2007，23:126-137.

［16］刘宝碇，赵瑞清，王纲.不确定规划及应用［M］.北京:清华大学出版社，2003:79-87.