柴油发电机组并联运行的混沌振荡分析

黄曼磊，刘宏达，许梦琪

(哈尔滨工程大学自动化学院，黑龙江哈尔滨150001)

船舶电力系统通常是多台柴油发电机组并联运行，具有高度的非线性，当系统运行点改变时，系统的动态特性会显著改变.在轻载工况运行时，船舶电力系统会发生非周期、貌似随机的、突发或阵发性的振荡现象，严重时会导致系统解列，这种现象称作混沌.混沌是非线性系统中各参数相互作用导致的一种非常复杂的现象，它在船舶电力系统中出现时，伴随着系统运行参数持续无规则的振荡，严重危害系统的运行安全，要在系统中有效地预防和消除它.为了对船舶电力系统的混沌现象进行分析，这里将建立2台柴油发电机组并联运行的数学模型，以准确地反映船舶电力系统的变化规律.在此基础上，利用Lyapunov指数法对船舶电站2台柴油发电机组轻载并联运行工况进行分析，寻找混沌产生的机理和原因，揭示其内在的变化规律，为预防和消除混沌打下基础.

1 柴油发电机组并联运行的数学模型

柴油发电机组的数学模型包括机电暂态过程的数学模型和电磁暂态过程的数学模型2部分，首先建立机电暂态过程的数学模型，然后建立电磁暂态过程的数学模型，这样在两者的基础上建立单台柴油发电机组的数学模型.

柴油发电机组机电暂态过程的数学模型描述了柴油发电机组的运动规律，反映了功角和角速度的动态变化过程，其表达式为

式中:δ为柴油发电机组功角，ω为柴油发电机组电角速度，U为发电机定子绕组端电压，Eq'为q轴暂态电势，X为绕组电抗，L为柴油机调速器执行器输出轴位移，ω0=100π rad/s，Ta、Tb、c1、c2为常数，δ、L为实在值，其余变量为标幺值.从式(1)可知，该方程具有非线性特征.

柴油发电机组电磁暂态过程的数学模型包括同步发电机定子电压平衡方程和励磁绕组电磁暂态方程，这里忽略阻尼绕组的作用，其表达式为

式中:U为定子绕组端电压，Ud和Uq为定子绕组端电压的d轴和q轴分量，R为定子绕组电阻，X为绕组电抗，I为绕组电流，T为绕组时间常数，Eq'为q轴暂态电势，Efd为励磁绕组电压.

由于Eq'不容易测量，这里选取定子绕组端电压U作为状态变量，只需将式(2)中的Eq'转换成U即可.根据变量数据之间的关系有:

将式(3)代入式(2)中的第1项得

将式(3)代入式(1)并与式(4)联立得

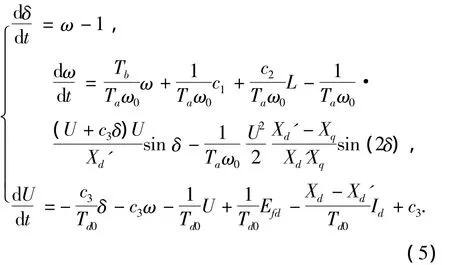
由电流Id的表达式可知

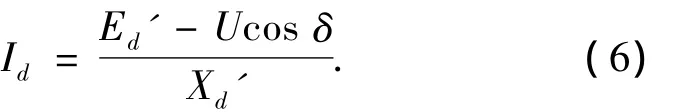
将式(3)代入式(6)中得

将式(7)代入式(5)中整理得

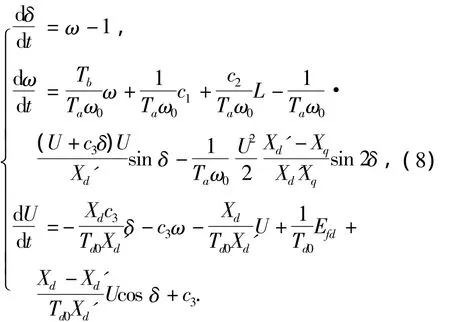
式(8)是单台柴油发电机组的非线性数学模型，该模型将功角、转速、电压相互作用、相互影响的关系反映出来，准确地描述了3个变量的变化规律［1-6］.

这里取第1台同步发电机的d-q轴为参考系，建立2台柴油发电机组并联运行的数学模型.假设2台柴油发电机组功率、型号和参数一致，负载电流的d、q分量为 Id、Id，2台同步发电机的功角差为δ12，则2台柴油发电机组并联运行的数学模型为

式中:i=1，2，下标1指第1台柴油发电机组，下标2指第2台柴油发电机组.

2台柴油发电机组的电流耦合关系为

式(10)描述了2台柴油发电机组并联后的电流分配关系.

2台柴油发电机组的电压耦合关系为

式(11)描述了2台柴油发电机组并联后的电压制约关系［7］.

式(9)～(11)是2台柴油发电机组并联运行的非线性数学模型，该模型将2台柴油发电机组相互作用、相互影响的关系反映出来，准确地描述了2台柴油发电机组功角、转速、电压的变化规律.

2 Lyapunov指数分析

这里以柴油发电机组的功角、转速、电压的变化规律来研究船舶电力系统的稳定性.由于并联运行的柴油发电机组之间存在一定的功率传递，很容易产生功率振荡.所谓功率振荡就是在某种周期性干扰的作用下，柴油发电机组进行反复功率调节的动态过程.

在负载功率不变的情况下，一台发电机功角的变化，必然使其他发电机的功角朝相反的方向变化，因此，影响并联机组稳定性的主要因素是发电机间的功角差.例如，发电机组的有功负载严重不平衡的时候，特别是一台发电机转入电动机工作状态，发电机间大的功角差，就有可能使并联运行失去稳定性.此外，在周期性干扰因素的作用下，如柴油机发火不均，周期性的冲击负载等，由于柴油发电机组之间调速系统或调压系统动作的不一致性，也会形成周期性的功角摆动，尽管这一摆动范围不一定会超越功角的极限值，但发电机组间的功率振荡却是相当可观的.

功率振荡从混沌的角度来看，实质上是一种混沌振荡.混沌运动的基本特点是运动对初始条件极为敏感，2个极其靠近的初值所产生的轨道，随时间推移按指数方式分离，Lyapunov指数就是描述这一现象的量.时间序列混沌特性的判别方法包括定量分析和直观分析，即先通过对Lyapunov指数的数值分析判断混沌出现的条件，再由直观分析法直观地确定在这种条件下混沌存在与否.直观分析法包括时间历程法、相轨迹图法、频闪采样法、Poincare截面法以及功率谱法.计算Lyapunov指数的方法主要有定义法、Wolf方法和Jacobian方法，其中Jacobian方法是一种在实际应用中发展起来的计算Lyapunov指数的方法.这里采用Jacobian方法计算Lyapunov指数［8-11］.

下面的微分方程系统:

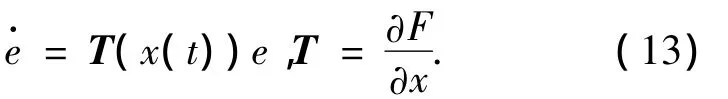
这里T是F的Jacobian矩阵.方程的解能够表示为

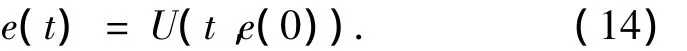
其中:U:e(0)→e(t)是线性算子映射.这个映射U的渐近行为用指数刻画为

所以，系统(12)的Lyapunov指数可以表述为上述重复过程的平均数:

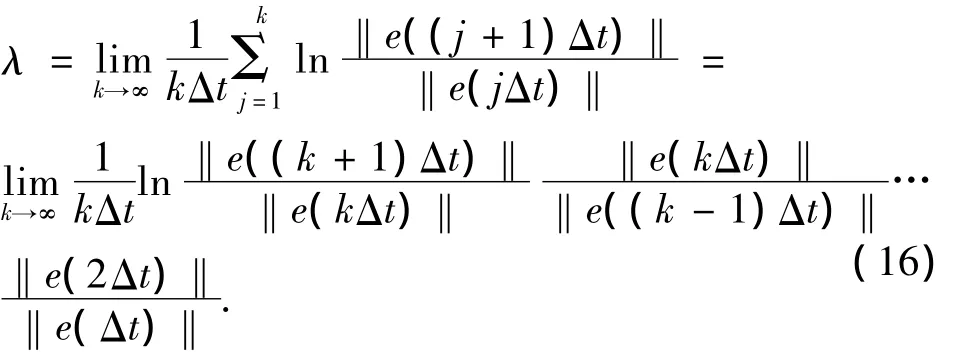
对于一个n维相空间，就会有n个Lyapunov指数，将它们按从大到小顺序排列，不妨设为(λ1≥λ2≥…≥λn)，其中λ1被称作最大 Lyapunov指数.一般来说，具有负的Lyapunov指数对应收缩方向，相邻轨道在局部是稳定的，对应周期运动.而正的Lyapunov指数表明相邻轨道指数分离，并在相空间中形成奇怪吸引子，Lyapunov指数λ越大，系统的混沌性越强，反之亦然.故对于n维相空间，最大Lyapunov指数是否大于0是判断系统是否出现混沌振荡的依据.

微分动力系统Lyapunov指数的性质对于三维情形，存在有如下6种吸引子

(λ1，λ2，λ3)=(－，－，－):稳定不动点;

(λ1，λ2，λ3)=(0，－，－):极限环;

(λ1，λ2，λ3)=(0，0，－):二维环面;

(λ1，λ2，λ3)=(+，+，－):不稳极限环;

(λ1，λ2，λ3)=(+，0，0):不稳二维环;

(λ1，λ2，λ3)=(+，0，－):奇怪吸引子.

对于柴油发电机组并联运行的非线性数学模型按照上述分析方法计算出3个Lyapunov指数λ1、λ2、λ3，形成 Lyapunov 指数谱.

3 计算机仿真结果

设 x1=δ，x2=ω，x3=U，则式(8)变为

分别对轻载并联运行的2台柴油发电机组的Lyapunov指数进行计算，2台柴油发电机组均采用常规的控制器.图1和图2分别给出了2台柴油发电机组并联带载12.5%的功角、转速、电压的相图.

图1 双机并联带载12.5%时1号柴油发电机组的相图Fig.1 Phase diagram of No.1 diesel-generator set when two sets load 12.5%on parallel connection

图2 双机并联带载12.5%时2号柴油发电机组的相图Fig.2 Phase diagram of No.2 diesel-generator set when two sets load 12.5%on parallel connection

2台柴油发电机组并联带载12.5%时运行100 s，1 号柴油发电机组的初值为:(δ，ω，U)=(0.101 7，1.066 2，0.976 2)，Lyapunov 指 数 为:λ1=0.076 789，λ2=0.035 235，λ3= －0.197 558;2号柴油发电机组的初值为:(δ，ω，U)=(0.102 2，1.066 2，0.976 2)，Lyapunov 指 数 为:λ1=0.076 806，λ2=0.035 230，λ3－0.197 571.

图3和图4分别给出了2台柴油发电机组并联带载25%的功角、转速、电压的相图.

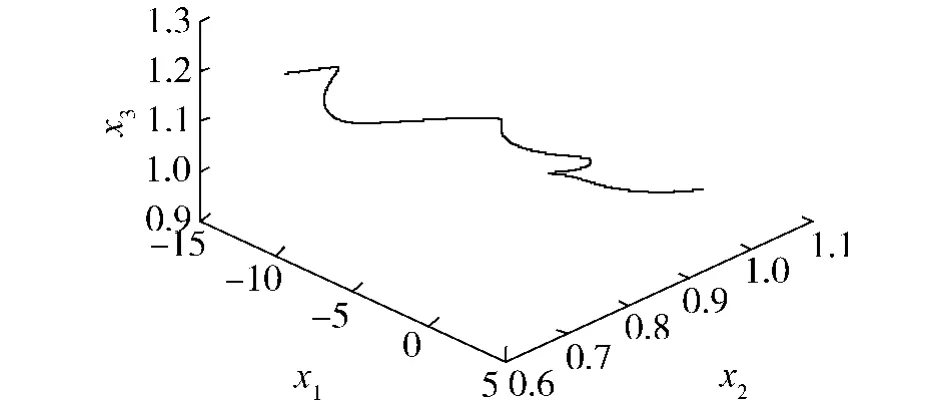
图3 双机并联带载25%时1号柴油发电机组的相图Fig.3 Phase diagram of No.1 diesel-generator set when two sets load 25%on parallel connection

图4 双机并联带载25%时2号柴油发电机组的相图Fig.4 Phase diagram of No.2 diesel-generator set when two sets load 25%on parallel connection

2台柴油发电机组并联带载25%时运行100 s，1号柴油发电机组的初值为:(δ，ω，U)=(0.181 2)，1.060 7，0.968 6)，Lyapunov 指数为:λ1=0.079 251，λ2=0.034 251，λ3= － 0.199 955;2号柴油发电机组的初值为:(δ，ω，U)=(0.182 01，1.060 7，0.968 6)，Lyapunov 指 数 为:λ1=0.078 311，λ2=0.034 953，λ3= －0.199 742.

从图1～4可以看到，系统最大Lyapunov指数均大于0，表明系统存在混沌现象.轻载并联运行的2台柴油发电机组，运行一段时间后，进入混沌状态，具体表现为功角和转速的振荡，2台柴油发电机并联带载越轻，功角和转速的振荡越剧烈.功角的振荡意味着功率的振荡，原因是船舶电力系统的非线性和2台柴油发电机组之间的功率传递.

图5、6分别给出了2台柴油发电机组并联带载25%加周期性负荷时的功角、转速、电压的相图.周期性负荷是船舶电力系统中经常会发发生的，也是很普遍的.

2台柴油发电机组并联带载25%加周期性负荷0.01 sin t时运行100 s，1号柴油发电机组的初值为:(δ，ω，U)=(0.181 2，1.060 7，0.968 6)，Lyapunov 指数为:λ1=0.073 257，λ2=0.031 824，λ3= －0.191 497;2号 柴 油 发 电 机 组 的 初 值 为:(δ，ω，U)=(0.182 01，0.060 7，0.968 6)，Lyapunov 指数为:λ1=0.073 393，λ2=0.030 161，λ3= －0.189 995.

从图5和图6可以看到，系统最大Lyapunov指数均大于0，表明系统存在混沌现象.同不加周期性负荷比较，2台柴油发电机组功角和转速的振荡更加剧烈.由于周期性负荷是非线性的，因此加入周期性负荷后加剧了系统的非线性，从而加剧了系统的功率振荡.

图5 双机并联带载25%加周期性负荷时1号柴油发电机组的相图Fig.5 Phase diagram of No.1 diesel-generator set when two sets increase period load meanwhile load 25%on parallel connection

图6 双机并联带载25%加周期性负荷时2号柴油发电机组的相图Fig.6 Phase diagram of No.2 diesel-generator set when two sets increase period load meanwhile load 25%on parallel connection

计算机仿真实验结果表明，2台柴油发电机组轻载并联运行时，存在混沌振荡现象，产生这种现象的主要原因是船舶电力系统的非线性，次要原因是2台柴油发电机组之间的功率传递.除此之外，采用常规的线性控制器也是导致系统产生混沌振荡的一个重要因素，只有采用非线性控制器，使船舶电力系统自身非线性特征得以抵消和补偿，才能从根本上解决系统混沌振荡的问题.混沌振荡现象是稳定状态与不稳定状态之间的过渡状态，必须加以预防，才能保证系统的稳定性.

4 结束语

船舶电力系统具有较强的非线性特征，2台柴油发电机组并联运行时容易产生功率传递，柴油发电机组采用常规的调压器和调速器，这3个因素的综合作用导致船舶电力系统混沌现象的发生.论文的结果对于柴油发电机组并联运行稳定性的研究具有一定的参考价值，为抑制或消除船舶电力系统中的混沌现象打下了坚实的理论基础.

［1］黄曼磊，唐嘉亨，郭镇明.柴油机调速系统的数学模型［J］.哈尔滨工程大学学报，1997，18(6):20-25.HUANG Manlei，TANG Jiaheng，GUO Zhenming.The mathematical model of diesel engine speed regulation system［J］.Journal of Harbin Engineering University，1997，18(6):20-25.

［2］黄曼磊，李殿璞，刘宏达.柴油机双脉冲调速器的仿真研究［J］.船舶工程，2002，24(3):36-38.HUANG Manlei，LI Dianpu，LIU Hongda.Simulation research on double-pulse speed governor of diesel engine［J］.Ship Engineering，2002，24(3):36-38.

［3］张汝均.船舶电站同步发电机的自动励磁装置［M］.北京:国防工业出版社，1989:158-219.

［4］韩英铎，王仲鸿，陈淮金.电力系统最优分散协调控制［M］.北京:清华大学出版社，1997:9-47.

［5］高国权.电站用柴油机调速系统［M］.北京:人民交通出版社，1983:8-78.

［6］倪以信，陈寿孙，张宝霖.动态电力系统的理论和分析［M］.北京:清华大学出版社，2002:72-90.

［7］л.п.维列捷尼柯夫.船舶电力系统暂态过程研究的理论和方法［M］.北京:国防工业出版社，1984:82-97.

［8］杨正瓴，林孔元.发电机的经典摇摆方程与混沌现象的初步研究［J］.电力系统自动化，2000，24(7):20-22，45.YANG Zhengling，LIN Kongyuan.Study on the relation between classical swing equations and chaos［J］.Automation of Electric Power Systems，2000，24(7):20-22，45.

［9］贾宏杰，余贻鑫，王成山.电力系统混沌现象及相关研究［J］.中国电机工程学报，2001，21(7):26-30.JIA Hongjie，YU Yixin，WANG Chengshan.Chaotic phenomena in power systems and its studies［J］.Proceedings of the CSEE，2001，21(7):26-30.

［10］王宝华，杨成梧，张强.电力系统分岔与混沌研究综述［J］.电工技术学报，2005，20(7):1-10.WANG Baohua，YANG Chengwu，ZHANG Qiang.Summary of bifurcation and chaos research in electric power system［J］.Transactions of China Electrotechnical Society，2005，20(7):1-10.

［11］朱志宇，刘维亭.船舶电力系统的数学建模和鲁棒控制器设计［J］.电机与控制学报，2007，11(3):291-298.ZHU Zhiyu，LIU Weiting.Mathematic model construction and robust controller design of decentralized excitation ship electrical power system［J］.Electric Machines and Control，2007，11(3):291-298.