开放式数控系统空间曲线插补跨卦限策略研究

刘有余，韩 江，田晓青，张国政

开放式数控系统空间曲线插补跨卦限策略研究

*刘有余1,2，韩 江2，田晓青2，张国政2

（1. 安徽工程大学先进数控和伺服驱动技术安徽省重点实验室，安徽，芜湖 241000；2. 合肥工业大学CIMS研究所，安徽，合肥 230009）

为简洁实现空间曲线插补，基于开放式数控系统研究插补跨卦限策略。规划了全软件CNC系统和NC嵌入PC系统插补模块的分子模块实现理论，以圆柱螺旋线和空间直线为例，研究了坐标仿射变换、自动跨卦限处理，及基本插补子模块调用的原理和技术。最后，用自行开发的全软件CNC系统进行了实例验证。实现了开放式数控系统插补模块单元化开发，兼顾了系统开放性与实时性，相关策略和原理亦可应用于其他空间曲线的插补。

空间曲线；跨卦限插补；开放式数控系统；仿射变换

基于PC的开放式数控系统有三种类型[1]：1) PC嵌入NC。在NC内部加装PC板，PC与NC之间以专用的总线相连接。2) NC嵌入PC。将运动控制器或整个NC单元插入PC扩展槽中，PC做非实时处理，实时控制由CNC单元或运动控制板来承担。3) 全软件CNC。CNC各项功能均由软件模块来实现，通过装在PC扩展槽中的接口卡来控制伺服系统。全软件CNC系统可实现CNC各层次的开放，是当今数控技术的发展方向；而NC嵌入PC系统具有良好的实时性，且开放性也较高，是高速高精数控系统的首选方案。

插补是数控系统核心模块，传统NC用硬件实现插补算法[2]，以确保插补任务的强实时性，现代PC运算速度已满足软件插补要求。插补算法一般均可实现空间直线和螺旋线（或圆弧）插补功能，有的还可实现抛物线或样条曲线插补。这些算法原理及其后改进已很成熟[3-4]，但应用于开放式数控系统的插补跨卦限技术尚未见报道。本文基于NC嵌入PC和全软件CNC开放式数控系统，统筹规划，以圆柱螺旋线和空间直线插补为例，研究空间曲线插补跨卦限策略与技术。

1 插补模块的功能实现策略

针对多坐标跨卦限加工轨迹，设计单个数控程序段经刀补后插补流程如图1所示。这是复杂空间曲线（如圆柱螺旋线）插补流程，空间直线经坐标仿射变换后可转化为不跨卦限情形，故流程中可略去“自动跨卦限处理”。

图1 插补模块执行流程

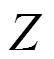
全软件CNC系统插补模块都用软件来实现，如图1所示，采用“数据处理与调用子模块”中断调用“基本插补子模块”（子程序）方式顺序执行。

基于提高插补实时性目的，NC嵌入PC系统插补模块采用软、硬件结合策略：“数据处理与调用子模块”以软件实现，编程与调试方便，并可分担硬件运算量；“基本插补子模块”以硬件实现，已有大量成熟的算法和可选购的产品[5]，无需另行研究和设计，且硬件插补运算速度较快。

2 坐标仿射变换

2.1 圆柱螺旋线坐标仿射变换

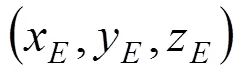
图2 圆柱螺旋线坐标仿射变换

Fig.2 Affine transformation for cylinder spiral-line

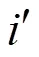
故：

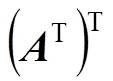
因此：

由仿射变换定理得：

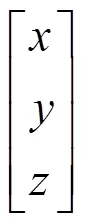
2.2 空间直线坐标仿射变换

图3 空间直线坐标仿射变换

Fig.3 Affine transformation for spatial line

3 圆柱螺旋线插补自动跨卦限处理

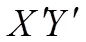
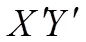
4 基本插补子模块调用

4.1 圆柱螺旋线插补子模块调用

圆柱螺旋线插补跨卦限流程如图5所示，首先初始化参数：终点′、进给速度、导程及旋向；其次判断旋向，若为右旋，从起点在′轴始，调用“基本插补子模块”的1子程序按周期进行插补，若期间到达终点，由1子程序判断并结束插补；1子程序运行完，经判断若未到达终点，调用2子程序进行插补，若到达终点则结束插补。如此依次调用3、4，当插完一个导程回至′轴还未到达终点，则继续调用1，如此反复。若为左旋螺旋线，插补流程类似，子程序调用次序为：4→3→2→1→4→……。

图5 圆柱螺旋线插补流程

4.2 空间直线插补子模块调用

在仿射坐标系中，空间直线是起点在原点、终点及整个直线都在某一卦限，避免了跨卦限。可针对终点在Ⅰ~Ⅷ卦限的典型直线编制8个插补子程序：1~S8，现有众多插补算法都可实现，如基于脉冲增量的快速直线双进给步增量算法[9]，精度好、误差小、计算简单、效率高，可采用该算法来编制。

图6 空间直线插补流程

5 实例验证

基于本文所述理论，自行开发出全软件CNC系统。轨迹显示界面如图7所示，在代码文本中按ISO格式输入CNC代码，可成功插补出圆柱螺旋线和空间直线。图例刀具插补轨迹为（-100.0，200.0，0）→（0.057，100.0，329.850）→（120, 100.0，329.850）→（100.0,200.0,0）。

图7 实例验证界面

6 结论

（1）规划了全软件CNC系统和NC嵌入PC系统插补模块的分子模块实现策略，将插补模块分“数据处理与调用子模块”与“基本插补子模块”，实现了开放式数控系统插补模块单元化开发，兼顾了系统开放性与实时性。

（2）以圆柱螺旋线和空间直线为例，研究了坐标仿射变换原理，将空间任意曲线变换为典型位置曲线；介绍了自动跨卦限处理方法，为应用基本插补算法提供基础；设计了基本插补子模块调用流程，实现了曲线空间简洁插补。

（3）本文理论和方法在自行开发的全软件CNC系统成功应用，相关策略和原理亦可应用于其他空间曲线的插补。

[1] 王太勇,乔志峰,韩志国,等.高档数控装备的发展趋势[J].中国机械工程,2011,22(10):1247-1259.

[2] Perfilieva I, Dubois D, Prade H, et al. Interpolation of fuzzy data: Analytical approach and overview Original Research Article [J]. Fuzzy Sets and Systems,2012,192(4): 134-158.

[3] 刘广瑞,王振超,毕竞锴,等.激光切割机的运动轨迹控制系统设计研究[J].郑州大学学报:工学版,2011,32(6): 75-78.

[4] Agrawal R K, Pratihar D K, Choudhury A R. Optimization of CNC isoscallop free form surface machining using a genetic algorithm [J]. International Journal of Machine Tools and Manufacture, 2006,46(7-8): 811-819.

[5] 姜峥嵘,王治森,董伯麟,等. 基于Windows CE.NET数控系统的插补控制[J].合肥工业大学学报:自然科学版,2006,29(12):1520-1524.

[6] Moustris G, Tzafestas S G. Reducing a class of polygonal path tracking to straight line tracking via nonlinear strip-wise affine transformation [J]. Mathematics and Computers in Simulation,2008,79(2): 133-148.

[7] 罗良玲,刘旭波. 基于时间分割法的圆柱螺旋线直接插补算法[J]. 南昌大学学报:工科版,2001,23(4):57-64.

[8] 刘有余,王立涛,付立新,等.虚拟数控轨迹仿真系统研究与开发[J].制造技术与机床,2009,5:66-69.

[9] Berriochoa E, Cachafeiro A, Brey E M. Some improvements to the Hermite–Fejér interpolation on the circle and bounded interval [J]. Computers & Mathematics with Applications, 2011,61(4): 1228-1240.

STUDY OF THE SPATIAL CROSS-OCTANT CURVE INTERPOLATION BASED ON OPEN CNC SYSTEM

*LIU You-yu1,2，HAN Jiang2，TIAN Xiao-qing2，ZHANG Guo-zheng2

（1. Anhui Key Laboratory of Advanced Numerical Control ＆ Servo Technology, Anhui Polytechnic University, Wuhu, Anhui 241000, China; 2. CIMS Institute, Hefei University of Technology, Hefei, Anhui 230009, China）

To simplify the interpolation for spatial curves, the strategy of cross octant is studied based on the open CNC system. The theory of the sub-modules of the interpolation for complete software CNC system or NC embedded PC system is built. Take the cylinder spiral line and the spatial line for example, some theories and techniques are studied and resolved including affine transformation, automatic cross-octant, and calling basic sub-modules of interpolation. Finally, an illustrative example is proposed to validate its feasibility and effectiveness. Furthermore, the interpolation module can be divided into some sub-modules to develop. The balance between the openness and the real-time is achieved. Some theories and methods in this paper can be also applied to other spatial curves.

spatial curve; cross-octant interpolation; open CNC system; affine transformation

TG659; TP273+.5

A

10.3969/j.issn.1674-8085.2012.05.015

1674-8085(2012)06-0065-05

2012-06-10；

2012-07-22

国家自然科学基金项目(51175001) ；“十二五”国家重大科技专项课题项目(2012ZX04001021)

*刘有余（1976-），男，安徽桐城人，博士生，主要从事现代集成制造系统研究(E-mail: liuyyu@ahpu.edu.cn)；

韩 江（1963-），男，河南洛阳人，博士，教授，博士生导师，主要从事现代集成制造系统研究(E-mail: hanjiang626@126.com)；

田晓青（1987-），女，山东淄博人，博士生，主要从事现代集成制造系统研究(E-mail:tianxq0617@163.com)；

张国政（1980-），男，安徽肥东人，博士生，副教授，主要从事现代集成制造系统研究(E-mail: zgzaust@163.com).