非圆信号二维DOA和初始相位联合估计方法

王 凌 李国林 谢 鑫 齐 率

(海军航空工程学院 烟台 264001)

1 引言

近年来利用目标空间中信源的信息冗余特性来提高空间谱估计的性能得到了广泛关注。信号的非圆性作为时域上的信息扩充，Galy首先将其引入空间谱估计研究中，提出了非圆信号测向的MUSIC算法[1](MUSIC algorithm for NonCircular signals,NC-MUSIC),Abeida和Delmas进一步对非圆信号MUSIC类测向算法的Cramer-Rao Bound (CRB)进行了分析[2]。近年来国内外不少文献对相关问题进行了研究[3－12]。目前，研究较多的一类非圆信号为直线信号，例如幅度键控信号和二进制相移键控信号等，其相位星座图沿直线分布，非圆率ρ=1。文献[3]中利用非圆信号为实值信号的特点，通过每次阵列快拍构造了一组数据矩阵，实现了非圆相干信号的完全解相干。文献[4,5]在构造的 Toeplitz矩阵中均利用非圆信号的共轭信息，降低了阵列孔径损失，提高了阵列自由度。文献[6,7]利用非圆信号椭圆协方差E[ss]≠0特性，构造虚拟阵元，提高了角度估计的精度。但上述算法模型背景中均假设非圆信号的初始相位为零，这在实际环境中几乎不可能满足。容易证明，非圆信号s(t)和其任意旋转s(t)ejφ具有不同的概率分布，因此对于非圆信号来说，初始相位不能忽略。如果考虑初始相位，上述基于非圆信号特性的算法均会存在估计性能下降的情况，特别是文献[3－5]中直接利用非圆信号的实值特性构造数据矩阵，当考虑到初始相位时，信号模型将不再满足实值特性，对算法的影响是严重的。近几年，部分文献对上述算法进行了修正[8,9]。

以上文献都是针对1维DOA估计的非圆算法，针对非圆信号背景下的2维DOA估计问题，公开文献中研究很少。仅有Haardt[13,14]等提出将2维酉ESPRIT用于非圆信号测向，以及刘剑[15,16]提出的基于双平行线结构的扩展 MUSIC算法。但是上述算法运算量都较大，需要构造维数为33MM×的数据矩阵，并进行特征分解。2维DOA和初相的联合估计可以看作是在3维参数空间进行点估计，基本思路是通过3维谱峰搜索实现，但运算量巨大。或者根据二次型的性质，将多维搜索转化为1维搜索或求根。

针对上述方法计算量大，且算法复杂的问题，本文提出了一种基于垂直阵列结构的任意初始相位非圆信号2维DOA和初相联合估计方法，利用阵列结构特点将3维参数估计转化为3个子阵上的2维参数估计问题，然后在每一个子阵列上，同时利用信号子空间的旋转不变性和噪声子空间的正交特性将2维估计转化为1维估计，且得到的2维DOA和初始相位能实现自动配对。该算法只需对 3个22MM×维的数据矩阵进行一次特征分解，且可在3个维度并行处理，相较于文献[15]中算法，运算量得到降低。由于利用了非圆信号特性，本文算法相较于具有相同阵列结构的文献[17]中算法，估计精度和可估计信源数都得到提升，且可估计多于阵元数的信源，最多可估计2(M−1)个信源。

2 阵列信号模型

考虑采用如图1所示的传感器阵列系统模型，该模型由3个相互垂直的均布线性子阵组成，记为，各子阵列阵元均为全向的，且阵列位于远场。第1个子阵由阵元0,1,…,M−1组成，第2个子阵由阵元0,1,…,N−1组成，第3个子阵由阵元0,1,…,P−1组成，各个子阵的阵元间距分别为dx,dy,dz。空间有D个相同载频的不相关窄带信源入射该阵列系统，信源数D假设为已知或已估计得到，波达方向矢量角分别为 (θ1,θ2,…,θD)，其中θk=(αk,βk,γk),αk,βk,γk分别为第k个源信号入射方向与x轴，y轴和z轴的夹角。显然有如下关系成立

可知3个角度变量中只有两个独立，因此，波达方向矢量角可以用1×2的矢量表示，即θk=(αk,βk)。称αk,βk分别为方位角和俯仰角。以阵元0为参考阵元，则子阵列Xa中第i个阵元的输出信号可表示为

其中sk(t)为第k个直线信号，,λ为其中心波长，nxi(t)为子阵列Xa中第i个阵元中的复圆高斯白噪声，噪声功率为σ2，且噪声与信源不相关。直线信号，其中φk为第k个直线信号入射到参考阵元的初始相位。文献[3－7]中均假定φk为零，然后利用实值性进行处理。本文考虑较为合理的情形，即各直线信号的非圆相位不全为零。

则子阵列Xa的输出信号矢量可表示为

式中

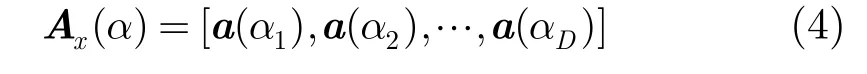
为M×D维阵列流型矩阵，a(αk)为对应的方向向量，且有

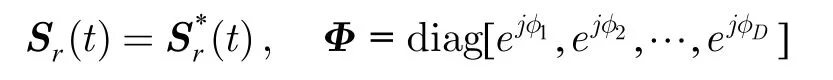
同理可以得到子阵列Ya和Za的输出信号矢量

式中

3 本文算法描述

本文算法主线是利用空间信号入射到垂直阵列后的阵列流型特点，将2维DOA和初相联合估计问题转化为3个可并行处理的2维参数估计，然后在每一子阵列上，同时利用信号子空间的旋转不变性和噪声子空间的正交性，通过一次特征分解得到的信号和噪声子空间将1维DOA和初始相位的2维搜索转换为1维估计问题，这样就把3维参数估计问题全部转化为1维估计，使算法运算量得到大幅的降低。

3.1 算法描述

受文献[13,18]启发，并利用非圆信号椭圆协方差非零特性，首先在x轴向构造

式中，ΠΜ为M×M维置换矩阵，其反对角线上元素为1，其余元素为0。,从bxk(αk,φk)的表达式中可以看出，此时已将(α,β,φ)的3维估计转化为(α,φ)的2维估计问题。改写bxk如下式

式中⊙为哈达玛积。从bxk的表达式不难发现，通过利用信号非圆特性构造式(14)等效于在x轴向的负向端扩展了一倍的阵列孔径，且扩展虚拟阵元的幅相增益为e−2jφk。按照上文思想，在y轴和z轴向同样构造扩展的观测矢量Gy(t)和Gz(t)，则经过扩展后的虚拟阵列结构如图2所示。

图2 扩展后的虚拟阵列系统模型

先计算x轴向的扩展协方差矩阵

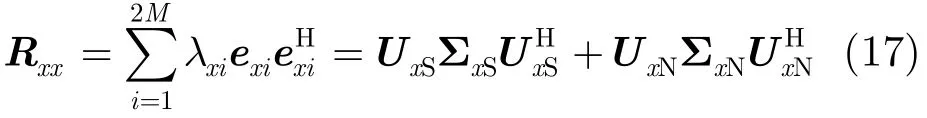
式中UxS为D个大特征值对应的特征矢量张成的信号子空间，UxN为2M−D个小特征值对应特征矢量张成的噪声子空间。如果直接利用噪声子空间的正交性进行估计，即x轴向的方向向量bxk与噪声子空间UxN正交，得到

由于噪声影响，式(18)并不完全接近于0，此时初始相位和1维DOA的估计就转化为最小化下式来实现

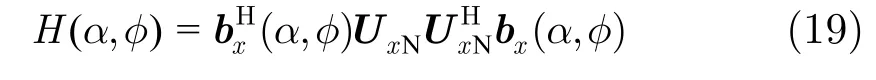
此时需要对α,φ进行2维搜索，为了避免复杂搜索，本文考虑在利用噪声子空间特性的同时使用信号子空间的旋转不变性来降维。以x轴向为例，扩展后的虚拟阵列如图3所示。经典的子阵划分方法为图中虚线所示。但由于非圆信号初始相位的影响，导致按图中虚线划分的子阵间将不再满足旋转不变性。由于虚拟阵元幅相增益的存在，可以考虑按实线方式进行子阵划分，此时

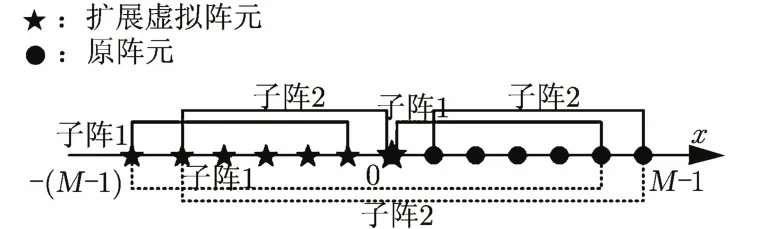
图3x 轴向子阵划分

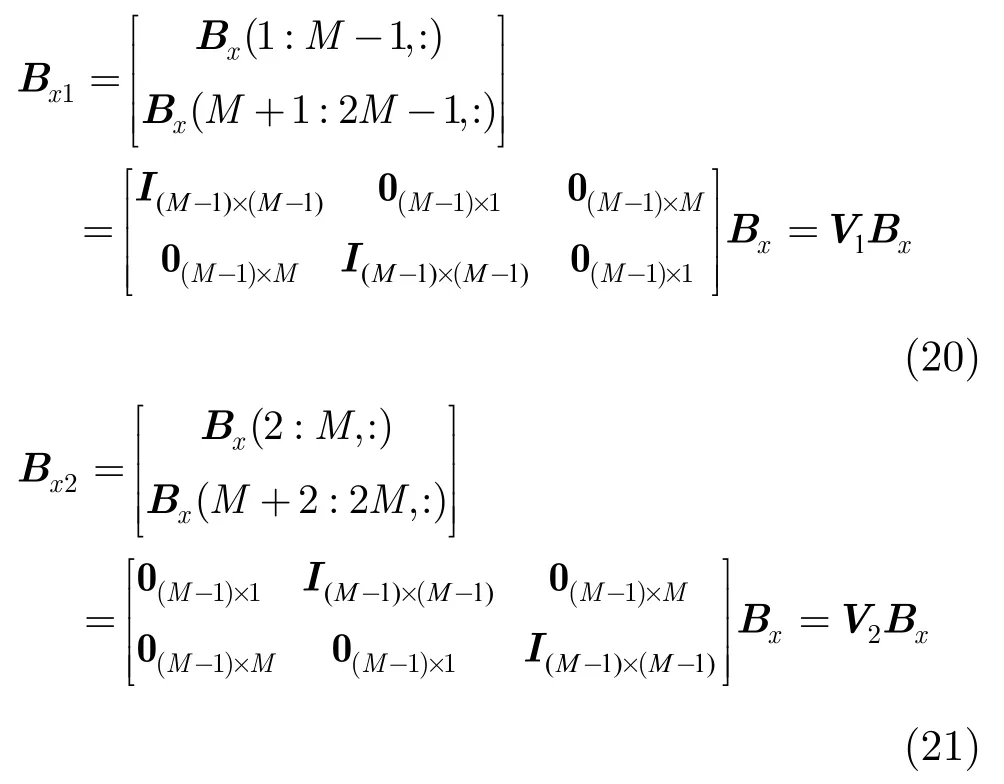
其中V1和V2为选择矩阵，同样令

因为Bx2=Bx1Ψx，其中Ψx=diag[u(α1),u(α2),…,u(αD)]，根据信号子空间旋转不变原理，易得：，其中Tx为一个非奇异转换矩阵，可得

利用最小二乘或总体最小二乘方法求解式(24)得到两子阵信号子空间之间的旋转不变关系矩阵Θx，通过对Θx特征分解得到的Ψx即可求得空间信源的方位角αk，然后将得到的αk代入式(19)，通过1维搜索即可求得对应于第k个信源的初始相位φk，这样就把(α,φ)的2维估计问题转化为两个1维估计。

同理，对另外两个轴向的旋转不变关系Θy和Θz进行特征分解可得到Ψy和Ψz，进而可计算出各个信号与y轴和z轴之间的夹角βi和γj。2维角度参数的配对可以通过计算d(k,i,j)的最小值来实现，d(k,i,j)的定义式为

3.2 算法步骤

由上文分析，可得到本文算法步骤如下：

(1)通过阵列天线获取垂直阵列的观测矢量X(t),Y(t)和Z(t)；

(2)根据式(14)形式构造扩展观测矢量Gx(t),Gy(t)和Gz(t)；

(3)计算扩展协方差矩阵Rxx,Ryy和Rzz；

(4)对扩展协方差矩阵进行特征值分解，得到各维度上相应的信号和噪声子空间；

(5)利用式(24)中信号子空间的旋转不变性计算信源与各轴之间夹角α,β和γ，并用式(25)进行配对；

(6)利用上步得到结果代入式(19)中，根据噪声子空间的正交性得到对应的初始相位φ。

4 数值仿真

为验证本文算法的有效性，从3个方面进行数值仿真验证，仿真中对比了具有相同阵列结构的文献[17]中算法。第1步验证本文算法对空间信源2维DOA和初始相位的联合估计性能；第2步验证本文算法对快拍数和信噪比的敏感度。最后验证本文算法的抗过载能力，即多于阵元数的信源估计能力。

4.1 2维DOA和初始相位联合估计验证

仿真1利用图1中的阵列系统模型，取阵元数M,N和P均为8，为避免估值模糊，阵元间距dx,dy和dz均取为λ/2。3个空间信号的2维到达方向分别为(30°,90°,60°),(60°,60°,45°),(85°,75°,1 5 .9°)。其附加初始相位分别为ejπ/6,ej2π/3和ejπ/3。信噪比为15 dB，快拍数为500，进行100次Monte-Carlo试验。图4(a)和4(b)就是采用本文算法得到2维DOA估计的星座图和初始相位的 MUSIC谱图。从仿真结果可知，本文算法能够准确地估计得到2维DOA和初始相位，并能实现自动配对。

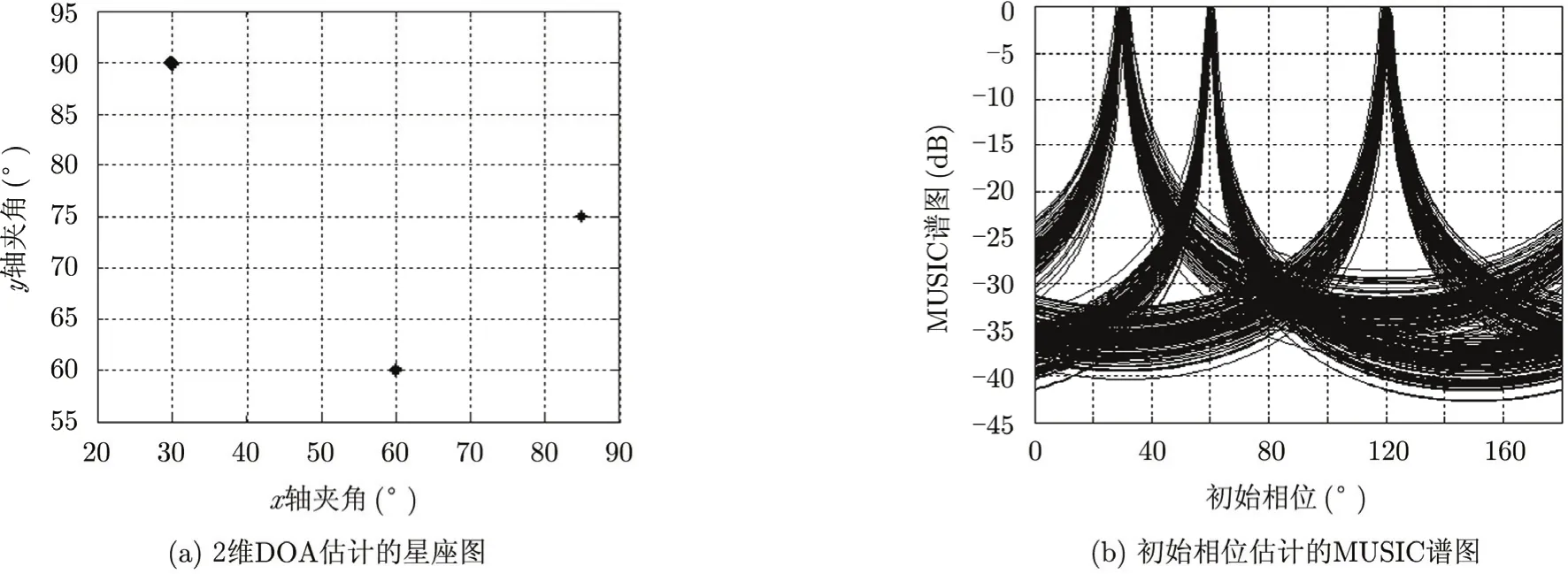
图4 2维DOA和初相联合估计

4.2 信噪比和快拍数对本文算法的影响

仿真1只是定性说明了本文算法的估计性能，下面通过两个仿真试验验证本文算法的估计均方根误差大小随信噪比和快拍数的变化趋势，并加入文献[17]中算法作为比较。

仿真2阵列和信号模型与仿真1相同，文献算法采用同样模型参数。快拍数固定为1000，改变信噪比，在0 dB到20 dB分别进行50次的Monte-Carlo统计试验，得到如图5所示的2维DOA估计性能与信噪比变化曲线。从图中可以看出，本文算法对每个信号的估计均方根误差都优于文献[17]中算法，并且随着信噪比的提升，算法估计误差逐渐减小。定义第k个信号的均方根误差为

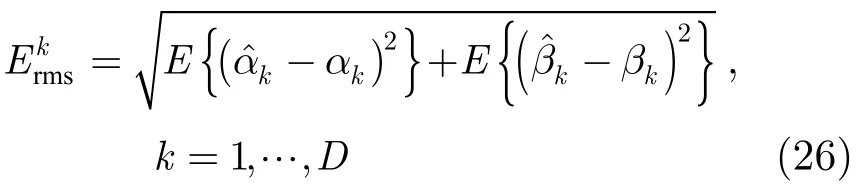
仿真3仿真参数同上。固定信噪比为5 dB，改变快拍数，在400次到1400次分别进行50次的Monte-Carlo统计试验，得到如图6所示的估计误差与快拍数变化曲线。从仿真结果可得，随着快拍数的增加，均方根误差逐渐减小，在快拍数高于900次后，误差趋于收敛。总体来看，本文算法在低信噪比和短快拍环境下，对2维DOA估计的均方根误差能控制在1°以内，且优于文献中算法。

4.3 阵列抗过载性能检验

由于使用了利用非圆信号特性构造的扩展观测矢量，因此本文能够估计的空间信源数为2(M− 1 )，能够对多于阵元数的空间信号进行估计，此时文献[17]中算法已经失效。

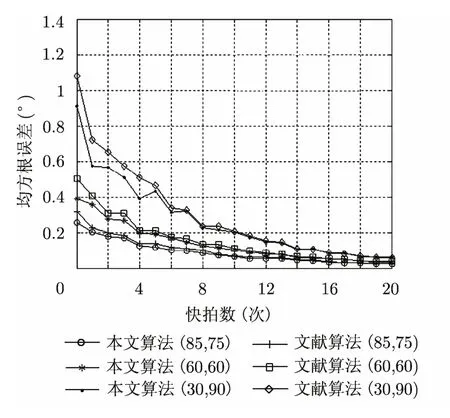
图5 估计误差随信噪比变化曲线

仿真4取阵元数M,N和P均为4，4个空间信号的2维到达方向分别为(30°,90°,60°)，(60°,60°,4 5 °),(85°,7 5 °,1 5 .9°),(70°,2 5°,7 5 .6°)。其附加初始相位分别为ejπ/6,ej2π/3和ejπ/3,和ej5π/6。信噪比为20 dB，快拍数为500，进行100次Monte-Carlo试验。图7(a)和7(b)就是采用本文算法得到2维DOA估计的星座图和初始相位的MUSIC谱图。此时阵列处于过载状态，传统的子空间估计方法失效，本文算法仍能准确得到结果。图7(a)和7(b)中不同来波方向信源的2维DOA和初始相位估计误差有区别的原因是仿真中采用了不同的信号形式。

5 结论

以往的2维DOA和初始相位联合估计问题，一方面需要复杂的3维搜索，另一方面需要对高维度数据矩阵进行特征分解运算，针对传统算法的复杂性，本文提出了一种基于垂直阵列结构的任意初始相位非圆信号2维DOA和初相联合估计方法，利用垂直阵列特点，将3维参数估计问题转化为可并行处理的3个2维参数估计，在每一个子阵上，同时使用噪声子空间正交性和信号子空间旋转不变性，将2维参数估计进一步转化为1维估计问题，最终只需要对协方差矩阵进行一次特征分解即可实现 2维DOA和初相的联合估计及自动配对。由于使用扩展观测矢量构造的协方差矩阵，本文算法适用于空间信源处于过载的情形和低信噪比、短快拍环境，因此适合多目标和干扰下对2维DOA和初相估计要求较高的机载、弹载阵列天线系统和小型地面阵列天线系统。数值仿真验证了本文算法的上述优良性能。

图6 估计误差随快拍数变化曲线

图7 过载环境下联合估计