一种新的随机PRI脉冲多普勒雷达无模糊MTD算法

刘 振 魏玺章 黎 湘

(国防科学技术大学电子科学与工程学院空间电子信息技术研究所 长沙 410073)

1 引言

传统的脉冲多普勒雷达发射周期性窄带脉冲串信号，利用离散傅里叶变换(Discrete Fourier Transform,DFT)实现多普勒滤波器组，对运动目标进行检测和测速[1,2]。然而，脉冲串信号的周期性不可避免地带来了测距和测速的盲区和模糊问题，常见的解决方案是通过发射多组参差脉冲重复频率(Pulse Repetition Frequency,PRF)的脉冲串信号，然后利用余数定理来解算模糊度[3]，目前国内外的脉冲多普勒雷达系统中也几乎都使用这种方案[4]。利用多组脉冲串进行联合串行处理，尽管可以实现解模糊功能，但对距离和速度的分辨率都没有提高，反而会加长相参处理周期(Coherent Processing Interval,CPI)，直接影响到雷达的工作效率。另一种可行的方案是在一组周期脉冲串信号的脉冲重复间隔(Pulse Repetition Interval,PRI)上叠加一个随机扰动，形成随机脉冲重复间隔(Random Pulse Repetition Interval,RPRI)雷达[5,6]。这种体制除了能够解决测距测速模糊及盲区效应以外，由于对信号引入了随机性，因而具有较强的低截获性能。然而，正是由于随机性的引入会导致回波相位的随机变化，传统的测速方法如离散傅里叶变换会产生随机的干扰频率成分，而随机雷达信号处理中常用的时域相关算法又会产生较高的旁瓣噪声基底。

压缩感知(Compressed Sensing,CS)理论[7－9]突破了传统奈奎斯特采样定律的限制，在稀疏成分分析的基础上对稀疏采样矩阵提出了更为宽松的充分条件，确保以比传统意义上少得多的观测数据对稀疏信号进行稳健精确的恢复。这套理论完备的信号处理新方法，为雷达信号处理提供了全新的思路，在雷达检测、估计及成像领域得到了广泛的研究[10－12]。由于其实质是一种参数化方法，旁瓣噪声基底主要取决于优化准则带来的微小估计误差，因此本身具有高输出信噪比的优点。考虑到RPRI雷达发射信号恰好满足该理论对稀疏观测矩阵受限等距性质(Restricted Isometry Property,RIP)条件的要求，且窄带雷达在同一距离和速度门上的有限目标个数也蕴含了回波信号的稀疏性，本文提出了一种新的全相参动目标检测(Moving Target Detection,MTD)技术。

文章主要结构安排如下：第 2节重点研究了RPRI雷达体制与压缩感知模型内在的对应关系，并分析了其动目标检测算法与性能；第3节详细讨论了RPRI雷达模糊消除技术，给出了不模糊测距测速的充分条件；第4节利用仿真实验从检测性能、测速精度和模糊特性等方面对算法的性能进行了全面验证；最后一节给出了结论并指出下一步工作展望。

2 基于压缩感知的RPRI雷达MTD技术

2.1 RPRI雷达波形设计与运动目标回波模型

对于RPRI雷达，设发射的相参脉冲串信号有M个宽度为T的脉冲，每个脉冲起始时刻偏离正常时刻mTr(其中Tr为正常PRI)的时间分别为Tm，则信号可以表示为

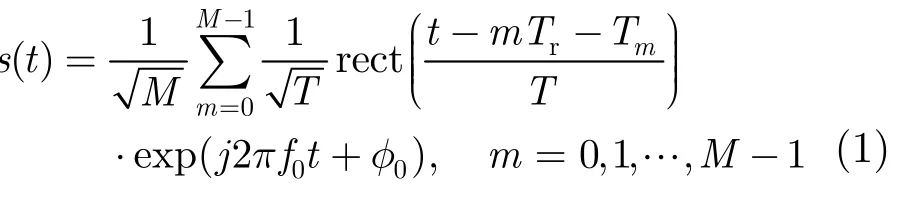
其中f0为载波频率，φ0为初始相位，

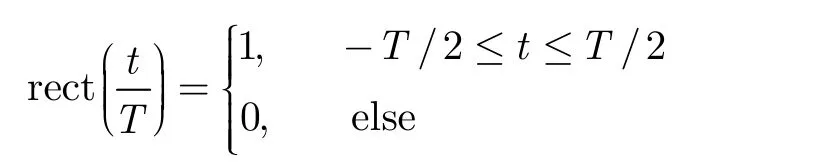
为单个矩形脉冲，T0=0 ,Tm(m=1,…,M−1)是服从某种随机分布的叠加扰动。本文主要研究一种特殊的离散型分布，即Tm为T的非负整数倍且不大于Tr−T，这种方式可以确保回波子脉冲的采样位置相同，更容易保证脉冲之间的相参性。其中最简单的一类就是二元伯努利分布，其分布律为

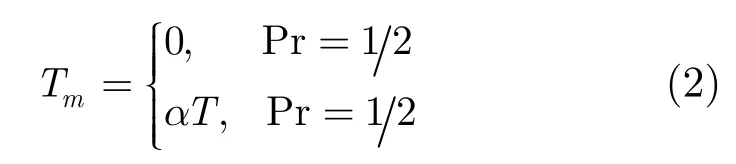
这里，α=1,2,…为非负整数且满足αT＜Tr−T，我们称之为扰动系数，Pr表示Tm的分布概率。此时脉冲重复间隔(m=0,…,M−1,TM=0 )同样为一随机变量，其分布律为

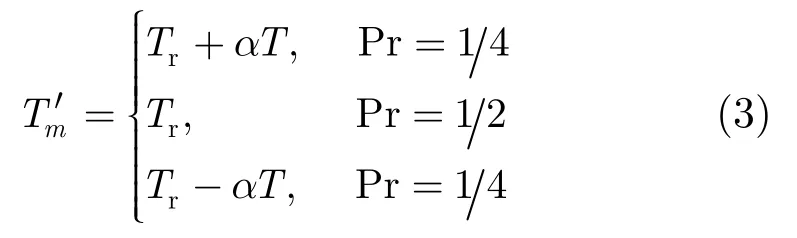
设同一距离门内K个目标的散射截面积(RCS)分别为Ak，与雷达之间的初始距离分别为R0k，目标分别以径向速度vk匀速直线运动(朝向雷达为正)，则将脉冲串信号的每个子脉冲回波与exp(j2πf0t)混频后得到

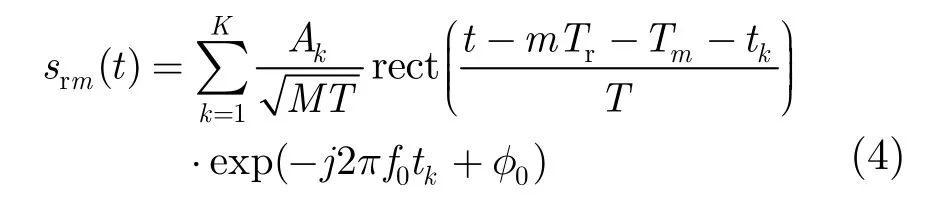
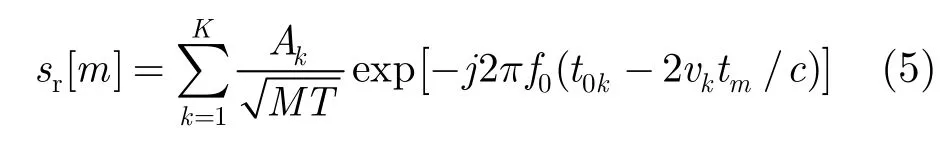
图1给出了最简单的RPRI雷达发射信号及其回波位置示意图，从图中可以看出，目标在每个脉冲周期内的回波位置决定于发射脉冲的位置，因此回波信号位置之间也没有了传统的周期性，使得目标的相位比周期 PRI信号多了一项在 0和4πf0vkαT/c之间切换的随机相位。

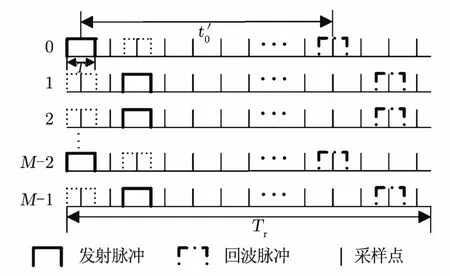
图1 2α=时的RPRI雷达信号示意图

2.2 传统方法的局限性分析

RPRI雷达回波信号由于其相位的随机变化使得DFT处理方法产生随机的干扰频率成分，而传统的随机信号处理方法——时域相关算法会在每个频率门产生随机的旁瓣，从而都会抬高多普勒频谱整体的噪声基底。

理论分析表明，由于随机相位的影响，在RPRI信号体制下，如果Tm和目标速度vk之间的关系使得mod(4πf0vkαT/c,2π)接近于0或者2π时，那么其引起的脉冲间的相对相位偏差不是很大，满足近似线性相位，用DFT算法和时域相关算法仍然能够得到目标比较精确的多普勒频谱。传统用于抗干扰的RPRI信号一般要求随机扰动幅度小于正常PRI的30%，也就是为了满足近似的线性相位[5]。文中所设计的用于解模糊的RPRI信号子脉冲之间的随机相位跳变通常更加剧烈，一旦其参数值使得mod(4πf0vkαT/c,2π)接近于π时，相位之间将完全没有线性特性，近似为随机相位编码。此时DFT算法会完全失效，而时域相关算法仍然有效，但会产生更大的噪声基底，降低目标的信噪比，影响目标的检测和测速性能。图2给出了两种特殊情况下常规的周期性PRI信号利用DFT处理的结果、RPRI信号利用DFT处理的结果以及RPRI信号利用时域相关(Correlation Processing,CP)算法处理的结果，与理论分析基本一致。

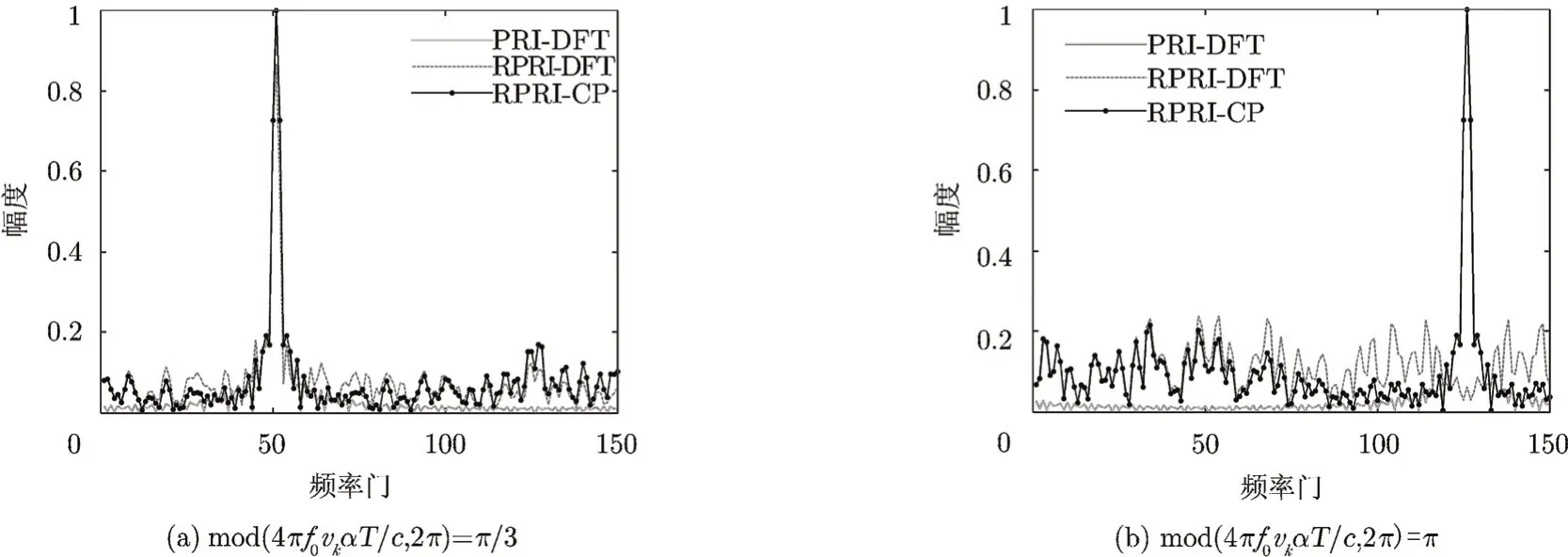
图2 两种特殊情况下规则PRI和RPRI信号不同算法的处理结果

2.3 基于压缩感知的RPRI雷达MTD算法

作为一种基于先验信息的参数化方法，压缩感知所带来的噪声基底主要取决于优化准则带来的微小估计误差，具有高输出信噪比的优点。我们下面研究利用压缩感知算法来估计目标的速度及回波强度，得到目标的多普勒频谱后，在频域进行动目标检测。

2.3.1 压缩感知理论

压缩感知理论突破了传统奈奎斯特采样定律的限制，在稀疏成分分析的基础上对稀疏采样矩阵提出了更为宽松的充分条件，确保以比传统意义上少得多的观测数据对稀疏信号进行稳健精确的恢复。下面首先简要介绍压缩感知的核心思想：

考虑抽象的欠定方程组为y=Ax+e(其中是一个满足(ε为一常数)的统计量或者未知确定量，压缩感知的可行性问题就等效为该欠定线性方程组的求解问题。对此，Candes等提出了一个确定解存在的充分条件，即矩阵A需要满足 RIP条件。对任何正整数S=1 ,2,… ,n，定义矩阵A的受限等距常数为满足下面条件的最小δS：

然而实际情况中，如何判断给定的矩阵是否具有RIP性质却是一个组合复杂度问题。为了降低问题的复杂度，文献研究指出如果选择高斯或者亚高斯随机矩阵(如伯努利分布)作为观测矩阵，当满足条件M≥O(Kl og(N/K))时，即可高概率保证RIP性质[13,14]。因此，压缩感知理论与随机性有着密不可分的关系，观测矩阵的设计和RIP条件的满足都有着随机的因素，目前也只有在随机性条件下才能严格满足压缩感知理论的前提需求。

2.3.2 基于压缩感知的运动目标检测及速度估计

考虑到式(5)也可以看作一个典型的欠定线性方程组，而且随机性的引入恰好使得等效的观测矩阵为一简单的亚高斯矩阵——伯努利矩阵，从而符合压缩感知理论中RIP条件的要求，因此基于随机PRI信号的速度估计问题就可以抽象为一个典型的压缩感知模型。考虑到噪声的影响，得到回波信号

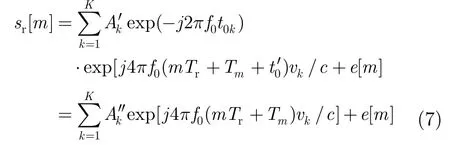
这一小节我们主要考虑目标距离和速度在传统意义上都不模糊的情况，把不模糊速度周期vu=λ/(2Tr)平均分成N(＞M)份得到速度分辨单元Vn=nΔv,n=0,1,…,N－1，Δv=λ/(2NTr)，式(7)可以写成矢量形式

U是一个M×N的亚高斯随机观测矩阵，其元素为Umn=exp[j4πf0(mTr+Tm)Vn/c]，向量a=[a0,a1,…,aN－1]T，也就是我们所说的多普勒频谱，其中当vk=Vn时,对应的an=Ak′ 而其余元素为0,e是功率小于ε的零均值测量噪声。根据压缩感知理论，当固定为某个速度分辨率(即固定N时)，只要满足M≥O(Kl og(N/K))，我们可以通过解下面的凸优化问题得到粗多普勒频谱像

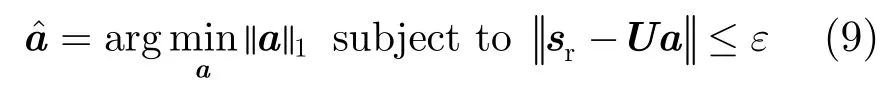
将模型实数化后求解得到目标的多普勒频谱后，在频域进行恒虚警处理[15]即可实现运动目标的检测，从而估计出目标的粗速度和回波强度。

3 基于参数设计的RPRI雷达模糊消除

前面我们只考虑了在传统意义上距离和速度都不模糊的情况。实际工作中，由于观测场景的复杂性，往往会存在距离和速度的模糊，即两目标的距离差为最大不模糊距离Ru=cTr/2的整数倍或者两目标的速度差为最大不模糊速度vu=λ/(2Tr)的整数倍。

3.1 距离模糊性分析

当距离存在传统意义上的模糊时，也即目标的回波跨越了脉冲重复间隔，由于发射脉冲之间没有严格的周期性，传统意义上的模糊目标与不模糊目标所在的距离门只有少部分重合，因此只要从采样后的信号中选择相应的距离门进行多接收通道处理，便不会出现模糊现象。如图 3(a)所示，假设两个目标(对应于回波1和回波 2)之间的模糊度相差1，则不妨设其所处的采样时刻即距离门分别为和(t0′=2R0′/c)，这种情况下只有当Tm=Tm+1时才会出现目标回波信号的重合；同理，对两个目标之间的模糊度相差p的情况，只有当Tm=Tm+p时会出现回波信号的重合。根据概率论，当只有两个模糊目标时，出现重合回波的概率约为 1/2；而随着模糊目标个数的增多，重合回波出现的次数也逐渐增多，对目标的测速和检测造成一定的干扰，此时可以根据实际工作需求改变Tm，使其分布在{0,T,2T,…}中，从而减小这种干扰的影响，图3(b)给出了PRI扰动满足简单的三元离散分布时雷达的模糊回波示意图。

同时我们可以看到，在使用这种信号体制时，由于发射脉冲不存在严格的周期性，传统意义上的盲距效应可以在一定程度上得到解决。

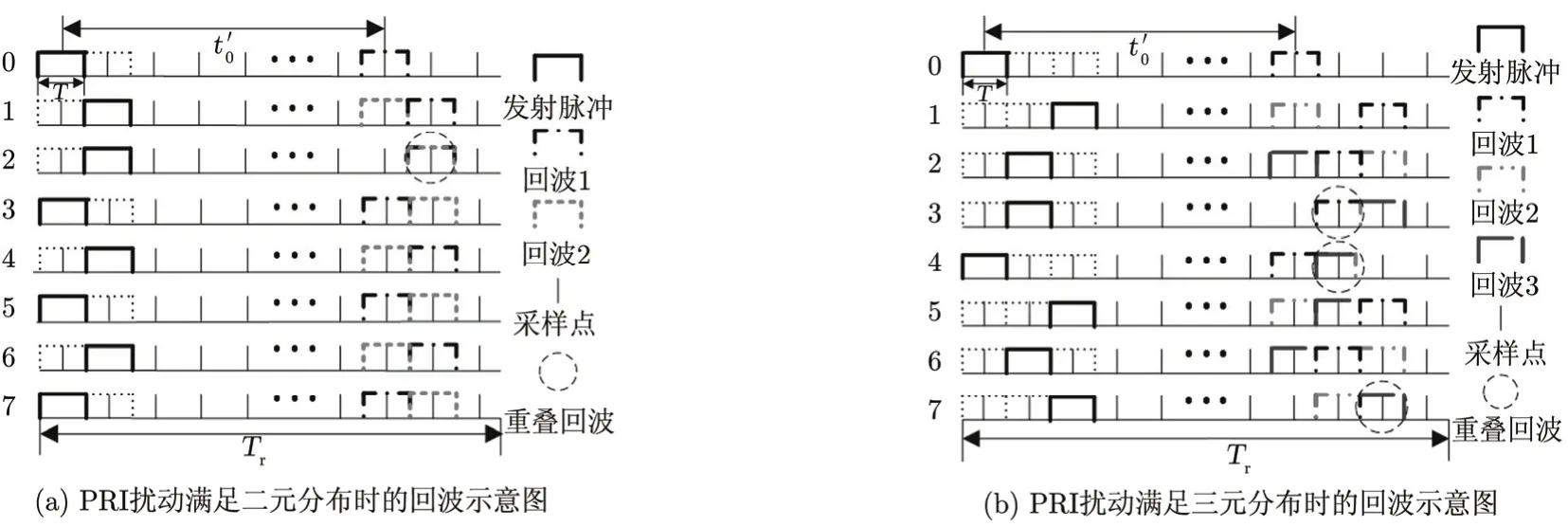
图3 目标距离模糊分析示意图

3.2 速度模糊性分析

当速度存在传统意义上的模糊时，也即目标的速度之间相差vu=λ/(2Tr)的整数倍，同样由于发射脉冲之间没有严格的周期性，模糊目标与不模糊目标对应的回波相位只有少部分相同，因此只要在速度域也使用多接受通道处理，按照我们所关注的目标速度范围vscope把接收机分为C=[vscope/vu]个并行通道，每个通道覆盖一个不模糊速度区间，起始速度值v0分别为 0,vu,2vu,…,(C－1)vu，对每个通道求解类似于式(9)中的的凸优化问题，得到相应的多普勒频谱，然后在多普勒域进行恒虚警检测，即可得到目标真实的速度。当两个目标传统意义上的速度模糊度相差q时，不妨设同一距离门内两个目标的速度分别为v0和v0+qλ/2Tr(0＜v0＜λ/(2Tr))，此时回波为

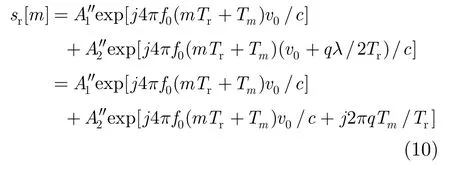
通过公式可以看到，正是因为第2个目标多了一项j2πqTm/Tr且Tm是一随机数，因此两者的回波相位并不完全相同，只有当Tm=0 时两个目标才会出现相同的回波信号相位，但这里必须指出当Tm相对于Tr较小且模糊度q较小时，两者相差的相位2πqTm/Tr都比较小，此时仍然存在一定程度的模糊，因此为了消除速度模糊，必须设置参数使得要解的模糊度q、随机扰动Tm和脉冲重复周期Tr满足mod(2πq α T/Tr,2π)接近于π。与距离模糊性类似，根据概率论，当只有两个模糊目标时，出现同相位回波的概率约为1/2；而随着模糊目标个数的增多，相同相位出现的次数也逐渐增多，对目标的测速和检测造成一定的干扰，此时同样可以根据实际工作需求改变Tm，使其分布在{0,T,2T,…}中，从而减小干扰的影响。

同样我们可以看到，在使用这种信号体制时，由于发射脉冲不存在严格的周期性，传统意义上的盲速效应也可以通过设定合适的波形及参数来克服。

4 实验结果与分析

本文采用 MATLAB软件进行仿真实验，验证雷达体制及算法的有效性。设雷达工作在X波段，波长λ=0 .03 m，发射周期性或者随机PRI相参矩形脉冲串，脉冲宽度为T=2 μs。本文中对式(9)的求解都使用CVX工具箱[16]实现。

4.1 检测性能分析

通过蒙特卡洛仿真分析比较基于压缩感知的检测算法和传统算法在不同信噪比下对运动目标的检测性能。设发射脉冲个数M=64，正常脉冲重复周期Tr=100 μs，扰动系数α=10，划分网格数N=150，虚警率为10－3。首先考虑只存在一个目标且目标随机分布在离散网格上没有粗糙损失的情况，对原始采样信号加入不同信噪比的高斯白噪声后进行处理。图4给出了RPRI信号分别用CP以及CS相参积累后在频域进行恒虚警检测的性能随信噪比的变化曲线，由于对于RPRI信号DFT算法在很多情况下会失效，这里为了对比给出了周期PRI信号用DFT处理的结果。由图可以看出，由于扰动系数不大，RPRI信号用时域相关算法的检测性能与周期PRI信号用DFT处理的结果相当，而利用压缩感知算法的检测性能有明显的提高，这是因为传统算法会产生较高的近旁瓣或者随机旁瓣噪声，从而影响多普勒频谱的信噪比，降低恒虚警检测性能；而在足够的信噪比条件下压缩感知算法对信号的恢复概率较高且产生的旁瓣基底较小，因此多普勒频谱的信噪比相对较高，从而目标的检测性能也较高。

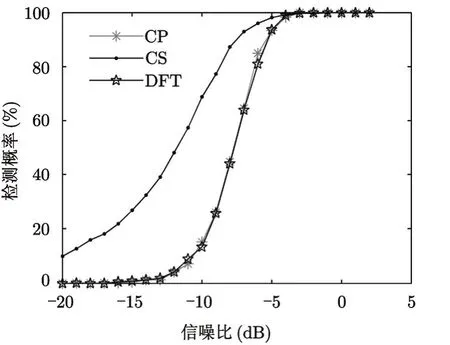
图4 不同算法下检测性能随信噪比的变化曲线

4.2 测速性能

上文中指出，随机PRI雷达信号理论上的速度分辨率可以达到c/(2f0NTr)，但由于压缩感知模型的求解受到N,M和K之间的相互制约关系，并不能通过增大N来无限制提高分辨率。要达到c/(2f0NTr)的速度分辨率，发射脉冲的个数M与目标个数K之间必须满足关系M≥O(Kl og(N/K))时，此时即可对目标高概率精确测速。

这里主要分析不同参数设置下精确测速的概率，仿真时没有考虑噪声的影响。定义恢复出的多普勒图像与原始设定目标之间的相关系数大于 0.9时为成功恢复，图5(a)给出了N=150(即固定速度分辨率)、蒙特卡洛次数为500、恢复概率 Pr为 95%时脉冲个数M和目标个数K所需要满足的关系。可见，要使得恢复概率达到95%，M至少大于40，而随着K的逐渐增大，M与K之间最多只要满足M≥5K就能保证；而当K大于70，即目标个数太多时，相比分辨单元数N=150已经不满足传统意义上的稀疏性，此时 CS算法性能下降，需要发射的脉冲个数要大于150。为了对比，给出了用CP的结果，由于旁瓣基底的影响，对于相同的目标数目所需要的脉冲个数要明显高于压缩感知算法，且当目标个数到达55附近时，算法性能就已经到达极限，不能对目标进行精确测速。图 5(b)进一步给出了N=150,M=64时，使用压缩感知算法的恢复概率Pr随目标个数K的变化关系。可见，当信号和所需分辨率固定时，随着目标个数K的增大，精确恢复的概率逐渐减小，从而影响检测和测速性能。由于实际情况中同一距离单元内目标个数不会很多(一般在 20个以内)，因此只要根据雷达应用背景选择合适的脉冲个数，就能保证算法的稳定有效。

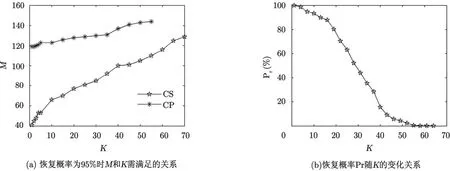
图5 不同参数设置下精确测速的概率

4.3 模糊性分析

这一小节主要分析信号参数设置对距离和速度模糊性的影响，同样不考虑噪声的影响。

4.3.1 距离模糊性能

假设存在两个传统意义上模糊度为1的目标，即有两个 RCS相同的目标距离对应的时延分别是t1m=mTr+Tm+t0′和t2m=(m+1)⋅Tr+Tm+1+t0′(t0′=2R0′/c)，速度分别位于第 75和第25个速度单元上。当使用传统的周期PRI信号时，在第1个目标真实距离门上得到的结果如图 6(a)所示，可以看出，由于脉冲之间具有严格的周期性，距离模糊现象十分严重，其中右边的目标为真实目标，左边的目标为模糊目标；当采用扰动系数α=10的二元随机分布RPRI信号时，由于回波重复的概率下降为原来的一半，模糊目标的强度也相应地下降为原来的一半，其结果如图 6(b)所示；而当采用随机分布在{0,T,2T,…,9T}的十元离散分布的 RPRI信号时，由于脉冲回波的重复概率进一步下降，几乎没有重复的脉冲，传统意义上的目标距离模糊特性也基本消失，如图 6(c)所示。因此当使用随机性较强的RPRI信号时，只要设定足够多的波门，则可以具有较大的不模糊测距范围。

4.3.2 速度模糊性能

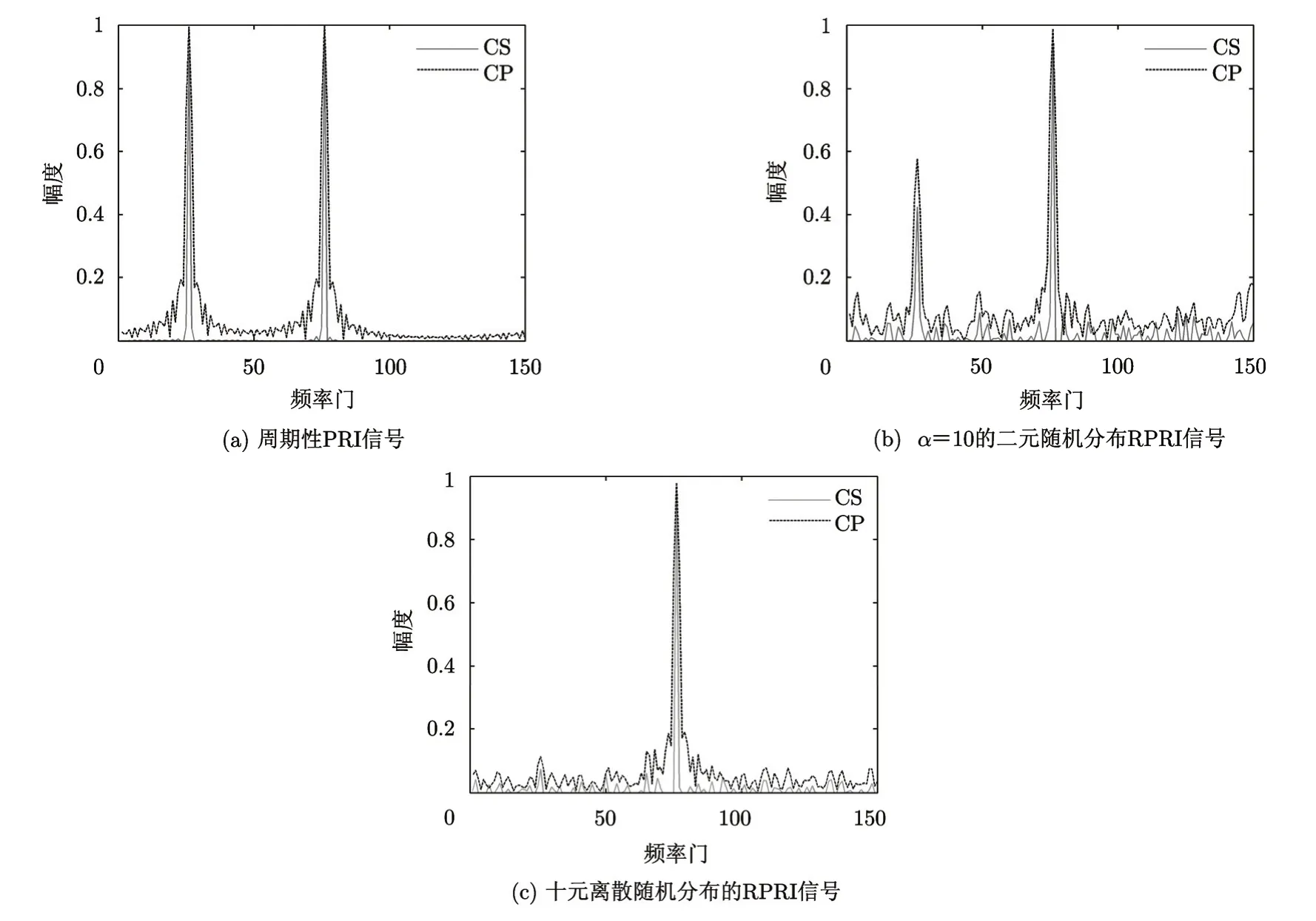
图6 不同信号的距离模糊性能

假设目标位于第 1个通道的第 75个速度单元上，图7分别给出了几种典型信号下通道0到通道9的测速结果。由图7(a)可以看出，当使用传统的周期PRI信号时，由于脉冲之间具有严格的周期性，在每个通道上都能检测到目标，目标速度完全模糊。当采用扰动系数α=25的二元随机分布RPRI信号时，由于 m od(2πqαT/Tr,2π)对于奇数q结果为π，偶数q结果为 0，因此在奇数通道上不模糊，而在偶数通道上完全模糊，其结果如图7(b)所示。而当采用随机分布在{0,T,2T,…,39T}的四十元离散分布的RPRI信号时，由于 mod(2πqαmT/Tr,2π)随机性较强，传统意义上的目标速度模糊特性也基本消失，如图7(c)所示。因此当使用随机性较强的RPRI信号时，只要设定足够多的通道，则可以具有较大的不模糊测速范围。

5 结论

本文提出了一种随机 PRI脉冲多普勒雷达MTD新技术，克服了传统周期性雷达存在的测距测速模糊和盲区效应，并且相比传统的多脉冲串参差重频方法而言，只需一个脉冲串，大大缩短了相参处理周期。压缩感知理论的应用能够较好地抑制随机性产生的旁瓣基底，提高目标的输出信噪比。仿真实验表明，该方案检测性能高、无距离/速度模糊、无测距/测速盲区，可大幅度提高雷达工作性能和效率，有望应用于各种新体制雷达中。下一步工作是进一步研究如何提高RPRI雷达的精确测速和杂波抑制性能。

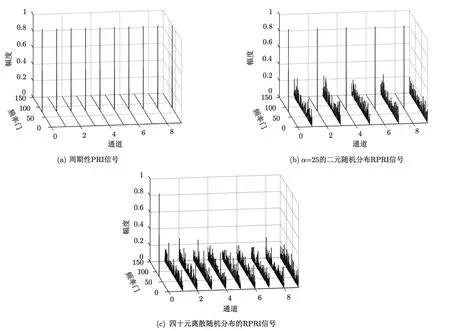
图7 不同信号的速度模糊性能