幂零群的若干充分条件*

孙文艳，钱方生

(哈尔滨师范大学)

0 引言

该文中群皆指有限群，所有术语和符号都是标准的.

樊恽、郭秀云等在文献［1］中提出了半覆盖远离性的概念后，引起了众多群论工作者的兴趣，不仅推广了C-正规的概念，而且推广了覆盖远离性的概念，并获得关于超可解的充分或必要条件.笔者利用4阶循环子群的半覆盖远离性和极小子群的一些基本性质，给出了幂零群的两个充分条件.

1 预备知识

定义1［1］设H是群G的一个子群，如果存在群G的一个主群列，1=G0＜G1＜… ＜Gt=G，使得对每一个 j=1，2，…，t，或者 H 覆盖Gj/Gj-1，或者H远离Gj/Gj-1，则称H在群G中具有半覆盖远离性.

定义2［2］称群G的元素x为群G中一个弱左Engle元，如果y是群G的任一阶与x的阶互素的素数幂阶元，则总有自然数n，使

引理1［3］设H是群G的一个子群，如果H在群G中具有半覆盖远离性，那么对任意满足H≤M≤G的子群M，H在群M中具有半覆盖远离性.

引理2［4］设群G为内幂零群，于是

(1)|G| 为 pαqβ，其中 p，q 为相异的素数.

(2)G=PQ，P ∈ Sylp(G)，Q ∈ Sylq(G)，P◁G，Q=〈a〉，不正规于 G.

(3)设c∈P，于是c是P的一个生成元的充分必要条件是c与a不可换.

(4)若P为交换群，则P为初等交换群.

(5)当p≠2时，exp(P)=p;当p=2时，exp(P)≤4.

(6)若 c为 P的一个生成元，则［c，a］ =c-1ca也是P的生成元.

(7)设N是群G真含在P内G的极大正规子群N= Φ(P)=P'，其中Φ(P)为Frattini的子群，P'为 P的导群 Z(G)=Φ(G)=Φ(P)×Φ(Q).

(8)P/Φ(P)是G/Φ(P)的极小正规子群.

证明 (1)至(7)显然的.

(8)假设结论不成立，设 P1/Φ(P)是G/Φ(P)的极小正规子群，而

则Φ(P)◁P1◁P，这与Φ(P)是含在P中的G的极大正规子群矛盾，故结论(8)成立.

引理 3［5］设 G 是有限群，a，b，c∈ G，则［a，b］c= ［ac，bc］.

推论 设G是有限群，a，b，c∈G，n是自然数，则

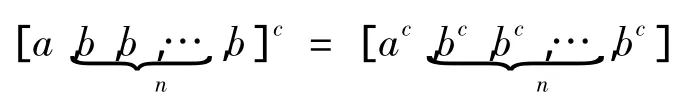
2 主要结果

定理1 如果群G的每个素数阶元都是群G的弱左Engle元，2∈π(G)，群G的每个4阶循环子群在群G中具有半覆盖远离性，则G幂零群.

证明 假设定理结论不成立，设G为极小阶反例.

由题设条件知子群遗传的，所以群G为内幂零群，由引理2知|G|=pαqβ，P∈Sylp(G)，Q∈Sylq(G)，P◁G，Q=〈a〉不正规于 G.

若p＞2，则由引理2知exp(P)=p，P有p阶生成元，由题设条件知，c为G的弱左Engle元，可得自然数 n，使，由引理2知［c，a］仍是P的生成元，产生矛盾.若P交换，则由引理2知P是初等交换群，同上知矛盾.所以p=2，P不交换.故P有4阶生成元c.由于群G是内幂零群，由引理2可知，P是G的正规子群，且P/Φ(P)是G/Φ(P)的极小正规子群.由题设条件知，〈c〉在G中具有半覆盖远离性，从而存在G的一个主群列，1=G0＜G1＜… ＜Gt=G，使得对每一个j=1，2，…，t，〈c〉或者覆盖Gj/Gj-1，或者远离Gj/Gj-1，由于c∈G，所以存在正整数k，使得c∉Gk，但是c∈Gk+1，于是Gk∩〈c〉≠Gk+1∩〈c〉，从而〈c〉覆盖 Gk+1/Gk，即 Gk〈c〉=Gk+1〈c〉=Gk+1.由P∩Gk◁G和P/Φ(P)是G/Φ(P)的极小正规子群，有(P∩Gk)Φ(P)=P或Φ(P).如果(P∩Gk)Φ(P)=P，则(P∩Gk)=P，这与c∉(P∩Gk)矛盾.故(P∩Gk)Φ(P)=Φ(P)，从而(P∩Gk)≤Φ(P)，再考虑G的正规子群，则有P=(P∩Gk+1)Φ(P)=(P∩〈c〉Gk)Φ(P)=〈c〉(P∩Gk)Φ(P)=〈c〉，这与P不交换产生矛盾.

故极小阶反例不存在，所以定理成立.

定理2 设N◁G，G/N幂零，2∈π(G)，若N的素数阶元均为群G的弱左Engle元，且N每个4阶循环子群也在G中具有半覆盖远离性，那么G幂零.

证明 假设定理结论不成立，设G为极小阶反例.

由题设条件知子群遗传的，所以G为内幂零群，由引理2 知 |G|=pαqβ，P ∈ Sylp(G)，Q ∈Sylq(G)，P◁G，Q=〈a〉不正规于 G.

(1)P≤/N中，则P1=P∩N◁P，而P1◁G，从而(P∩N)Q=P1Q＜PQ=G，于是P1Q为幂零群，所以 P1Q =P1×Q，G/P1=P/P1·QP1/P1，QP1/P1∈Sylp(G/P1)为幂零群.由G/P及G/N幂零，知G/P1幂零，所以QP1/P1◁G/P1，所以Q char QP1◁G，从而Q◁G，与引理2中Q循环矛盾.

(2)若p＞2，则exp(P)=p，P有p阶生成元c.由定理条件知，c为群G的弱左Engle元，即可得自然数n，使.由引理2知［c，a］仍是 P 的生成元，产生矛盾，p=2，P 不交换.

(3)由题中条件知，P有4阶生成元c.由于群G是内幂零群，由引理2可知，P是G的正规子群，且P/Φ(P)是G/Φ(P)的极小正规子群.由题设条件知，〈c〉在G中具有半覆盖远离性 ，从而存在G的一个主群列，1=G0＜G1＜… ＜Gt=G，使得对每一个 j=1，2，…，t，〈c〉或者覆盖Gj/Gj-1，或者远离 Gj/Gj-1，由于 c∈G，所以存在正整数k，使得c∉Gk，但c∈Gk+1，于是Gk∩〈c〉≠Gk+1∩〈c〉，从而〈c〉覆盖Gk+1/Gk，即Gk〈c〉=Gk+1〈c〉=Gk+1.由 P ∩ Gk◁G 和 P/Φ(P)是G/Φ(P)的极小正规子群，有(P∩Gk)Φ(P)=P或Φ(P).如果

(P ∩Gk)Φ(P)=P，则(P∩Gk)=P，这与c∉(P∩Gk)矛盾.(P∩Gk)Φ(P)=Φ(P)，从而(P∩Gk)≤Φ(P)，再考虑G的正规子群，则有P=(P∩Gk+1)Φ(P)=(P∩〈c〉Gk)Φ(P)=〈c〉(P∩Gk)Φ(P)=〈c〉，这与P不交换产生矛盾.所以P＜N.

(4)b∈ N，|b|=q，由引理 2知 G的Sylow-q子群都循环，故G的Sylow-q子群的q阶元都共轭，所以对任意g∈G，有bg肯定是群G的某个Sylow-q子群的q阶元.由P◁G知对任意c∈P，g∈G，有cg∈P.由题条件知b为G的弱左Engle元，即存在正整数n，使.由此可知，G的所有q阶元都为G的弱左Engle元.

(5)若p=2知G的2阶元和4阶元均为G的弱左Engle元，从而4阶循环子群在群G中具有半覆盖远离性，由(4)和定理1知G为幂零群，产生矛盾.

故极小阶反例不存在，所以定理成立.

［1］ 樊恽，郭秀云，岑嘉评.关于子群的两种广义正规性的注记［J］.数学年刊，2006，27A(2):169-176.

［2］ 王坤仁.极小子群与幂零性［J］.四川师范大学学报:自然科学版，1995(2):16-20.

［3］ Guo X Y，Guo P F，Shum K P.On semi coveravoiding subgroups of finite groups［J］.Journal of Pure and Applied A lgebra，2007，209.151-158.

［4］ 陈重穆.内外ε-群与极小非ε［M］.重庆:西南师范大学出版社，1998.

［5］ 徐明耀.有限群导引(上)［M］.北京:科学出版社，2001.