利用T/P卫星高度计资料调和分析南海潮汐信息

赵云霞, 魏泽勋, 王新怡

(1. 海洋环境科学和数值模拟国家海洋局重点实验室, 山东 青岛 266061; 2. 国家海洋局 第一海洋研究所,山东 青岛 266061)

利用T/P卫星高度计资料调和分析南海潮汐信息

赵云霞1,2, 魏泽勋1,2, 王新怡1,2

(1. 海洋环境科学和数值模拟国家海洋局重点实验室, 山东 青岛 266061; 2. 国家海洋局 第一海洋研究所,山东 青岛 266061)

利用j, v模型调和分析1992～2002年共10 a的TOPEX/Poseidon(T/P)海面高度距平资料, 提取了南海K1, O1, P1, Q1, M2, S2, N2和K2等8个主要分潮的潮汐调和常数。分析比较了卫星上下行轨道的19个交叉点的振幅和迟角, 其中M2, S2, K1和O1的平均向量均方根偏差分别是1.5, 1.1, 2.5和1.4 cm;将交叉点的调和常数与TPXO7.2模式的结果进行了比较, 结果表明M2, S2, K1和O1分潮振幅的绝对平均误差均小于3 cm, 迟角的最大绝对平均误差为7.8°。选取了与卫星轨道较近的8个验潮站, 对验潮站的实测数据调和常数和本文所得调和常数进行了比较, 结果显示K1分潮的向量均方根偏差为4.7 cm,M2分潮的向量均方根偏差为3.7 cm。论文结果表明利用j, v模型调和分析方法对南海海域卫星高度计资料进行潮汐信息提取是可靠的, 并可为局部重力场的研究提供海洋潮汐改正数据, 有一定的参考价值。

潮汐; 南海; TOPEX/Poseidon; j, v模型调和分析

高度计是测量地球表面相对高度的仪器, 广泛应用于海流、海浪、潮汐、海表面风场等海洋现象的研究。卫星高度计测量的海面高度本身需要进行潮汐修正, 可从中提取潮汐信号, 并应用于潮汐研究。

卫星高度计的发射, 特别是 1992年 TOPEX/Poseidon(以下简称 T/P)卫星高度计的发射并投入使用, 以及伴随着潮波数值模式和数据同化方法的发展, 使得卫星高度计提取的潮汐调和常数达到了高精度。Mazzega 等[1]利用卫星高度计资料结合验潮站数据, 反演了亚洲半封闭海的潮波系统(CSR模式)。Morimoto等[2]利用 T/P资料提取了日本海主要分潮的调和常数, 证明了利用高度计资料研究日本海潮汐特征是可行性的。李立等[3]对高度计资料进行了潮汐混淆的分析。董晓军等[4]利用T/P高度计资料调和分析得到了黄海、东海的潮汐信息。李燕初等[5]采用正交响应法导出福建和台湾邻近海域的潮汐特征。Fang等[6]利用10 a的T/P资料提取了渤、黄、东海的主要分潮的调和常数, 并结合验潮站信息, 给出了比之前相关研究更准确的渤、黄、东海的主要分潮的同潮图。

关于南海潮波系统的研究, 很多学者做了大量的工作, Yanagi等[7-8]直接从卫星高度计资料中提取中国海主要潮汐分潮的调和常数; Fang等[9]利用数值计算的方法对南海的主要分潮进行了数值模拟研究, 并分析了南海潮波的传播分布变化规律; 暴景阳等[10]讨论了由卫星测高数据进行潮汐分析的混叠问题和分潮的可分辨性, 采用了测高轨迹交叉点数据进行调和分析, 用不同方法验证了计算结果的精度; 毛庆文等[11]用T/P, T/P-J高度计资料调和分析得到了南海的潮汐信息; 李培良等[12]利用正交响应法对南海T/P卫星资料进行了分析, 得到了3个主要全日分潮(K1, O1, P1)和3个主要半日分潮(M2, S2, N2)的调和常数; 吴自库等[13]利用伴随同化数值模拟方法将 T/P资料同化到二维潮汐数值模式中模拟计算了南海的m1和M2分潮; Tian等[14]利用T/P资料估算了西北太平洋沿岸的 M2内潮能通量; 汪一航[15]利用16 a以上的T/P-J卫星高度计资料获得了南海主要分潮的调和常数。本文基于 10a的卫星高度计的测高沿轨数据, 利用j,v潮汐模型的最小二乘调和方法提取南中国海的潮汐信息, 验证了j,v模型调和分析南海潮波的可靠性。

1 资料来源及处理方法

1.1 卫星测高数据的分潮混淆

T/P卫星高度计轨道的重复周期是9.9156 d, 在此期间卫星绕地球旋转127圈, 根据Nyquist采样定理, 采样的时间间隔大于信号的半周期时会产生频率混叠效应, 在频谱上形成虚假的谱峰, 造成高、低频分量间的混乱, 即高频混淆, 表1给出了所研究的8个主要分潮各自的混淆周期。利用卫星高度计资料进行潮汐信息提取的误差主要来自高度计取样过程引入的高频混淆。由于高频混淆, 我们难以用常规的潮汐分析技术分离高度计资料中的潮汐分量, 按照Rayleigh准则, 两个频率的潮汐信号实现可靠分离所需要的时间T应满足

其中Ti和Tj为所比较的2个分潮的周期。由此计算得出8个主要分潮基本的分辨时间, 见表2[3]。

由表2可以看出, 区分M2和S2分潮, 需要2.97 a的数据, 区分K2和P1分潮, 需要约9.18 a的数据,该时间是8个主要分潮中分辨两个分潮所需要的最长时间。因此, 要获取M2, S2, N2, K2, K1, O1, Q1和P1稳定的调和常数, 至少要9.18 a的采样时间。因此, 本文采用法国国家空间中心提供的 1992年至2002年共计10 a的海面高度的沿轨数据, 可以对以上主要分潮进行调和分析。本文所研究的区域范围为 5°～25°N, 105°～125°E, 该范围包含了 9 条上行轨道和 10条下行轨道, 研究区域卫星测高轨迹见图1。

1.2 数据的处理方法

在利用卫星高度计资料时首先要对测得的资料进行校正, 高度计测得的相对于固体地球表面的海面高度为:

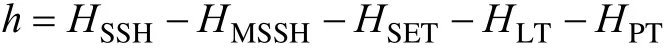
其中,HSSH是相对于基准椭球面的海面高度,HMSSH是平均海平面高度,HSET是固体潮潮高,HLT是负载潮潮高,HPT是极潮潮高[6]。

表1 主要分潮的周期及在T/P采样的混淆周期Tab. 1 Tidal periods and TP alias periods

表2 主要分潮基本的分辨时间Tab. 2 TP alias synodic periods of each pair of constituents

图1 研究区域的地形图及卫星海面轨迹Fig. 1 Map of the South China Sea and T/P ground track

2 利用j, v模型进行潮汐的调和分析

随着科学技术的发展, 特别是天体测量技术的飞速发展, 天文变量的计算精度也不断提高。霍恩在1967年考虑了太阳分潮的对月球轨道影响, 提出了j,v模型[17]。陈宗镛等[18]经过大量试算, 给出了58个分潮的j, v公式, 并进行了二次分析, 消除了噪声的影响, 促使这一模型理论上更加严格。本文主要针对M2, S2, N2, K2, K1, O1, P1和Q1这8个主要分潮, 采用j, v模型进行调和分析。

假设经过各种误差修正后, 卫星高度计获得的海面高度为h, 则有,

其中,0S为该点的平均海平面,s为该点海平面的时间变化部分, 主要成分是海洋潮汐。

采用的j, v模型为如下:

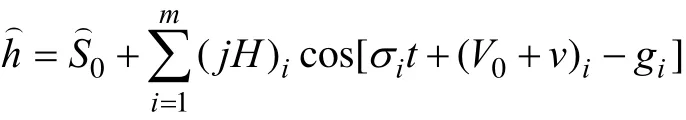
其中,t为每日零时起算的观测时刻,σ为分潮的角速率,H为分潮的振幅,g为格林威治迟角(文中涉及的角度均为格林威治迟角),H和g合称分潮的调和常数,j为分潮的交点因子,0( )Vv+ 为分潮的幅角, 在本文中我们主要提取8个主要分潮, 即m=8, 8个主要分潮的j,v公式参照陈宗镛[17], 在此不详细列出。

3 结果分析

3.1 交叉点上下行轨道的调和常数的比较

经过以上调和分析, 可以得到卫星重复轨道交叉点的调和常数, 8个主要分潮上下行轨道的计算结果见表3及表4, 其中,

La,Ld,ga及gd分别为交叉点上下行轨道的平均振幅和平均迟角,Δ表示每个交叉点的向量均方根偏差,k表示交叉点的个数,ΔRMS表示该分潮在南海所有交叉点的平均向量均方根偏差,ΔRMS越小表示上下行轨道调和的结果相关性越强。

表3 交叉点上下行轨道全日分潮结果比较Tab. 3 Difference between harmonics derived from ascending and descending passes at crossover points: diurnal tides

表4 交叉点上下行轨道半日分潮结果比较Tab. 4 Difference between harmonics derived from ascending and descending passes at crossover points: semidiurnal tides

通过对南海19个交叉点上下行轨道调和常数的计算结果的分析比较, 全日潮K1和O1的平均振幅分别为36.6 cm和35.1 cm, 而半日潮M2和S2的平均振幅分别为17.2 cm和6.7 cm, 由此可计算出

其中,1KH,1OH和2MH分别表示K1, O1和M2的平均振幅, 可以看出南海大部分海区呈现比较明显的全日潮特征[16]。在交叉点M2, S2, K1和O1的平均均方根偏差分别为1.53, 1.15, 2.57和1.41 cm, 可以看出上下行轨道在交叉点处的计算结果符合良好。

3.2 与TPXO7.2计算结果的比较

TPXO7.2模式是美国俄勒冈大学Egbert等利用T/P卫星资料和二维线性潮波模式建立的全球大洋潮汐同化模式, 利用Laplace潮波方程和包含测量资料的泛函的最优解, 提取了全球8个主要分潮和9个次要分潮的调和常数[19-20]。这里利用TPXO7.2结果对j,v模型计算的调和常数(上下行轨道的平均值)进行了验证, 结果见表5。

这里的ΔH,Δg为TPXO7.2结果与j,v模型计算结果中振幅和迟角的绝对误差, 可以看出四个主要分潮的振幅的绝对平均误差均小于 3 cm, 迟角的最大绝对平均误差为7.78°, 可见j,v模型计算结果与TPXO7.2模式结果一致性较好。

在南海研究区域任选两个点, 比较 TPXO7.2的8个主要分潮的调和常数和j,v模型计算结果, 具体见图2。

比较结果表明, 对于随机选取的这两个点的 8个分潮调和常数, 本文结果与TPXO7.2结果符合良好。这进一步验证了基于高度计资料利用j,v模型调和分析南海潮汐信息的可靠性。

3.3 与验潮站实测资料的比较

由于卫星的轨道间隔比较大, 为了进一步验证j,v模型的计算结果, 我们将调和分析得到的两个主要分潮 K1, M2的调和常数与 8个沿岸验潮站(位置见图1)资料进行了对比。表6给出了j,v模型计算结果与沿岸验潮站实测结果的对比情况。

从表6可以看出j,v模型计算结果与验潮站实测结果差别不大, 进一步分析可知, K1分潮振幅的绝对平均误差为2.6 cm, 迟角的绝对平均误差为7.1°, 其向量均方根误差为4.71 cm; M2分潮振幅的平均绝对误差为2.0 cm, 迟角的平均绝对误差为3.7°, 其向量均方根误差为 3.76 cm。由于验潮站多在近海区域,近海区域地形变化较为复杂, 卫星高度计调和分析结果与计算结果存在一定差异。经过以上比较, 向量均方根误差均小于5 cm, 进一步验证了j,v模型计算结果是可靠的。

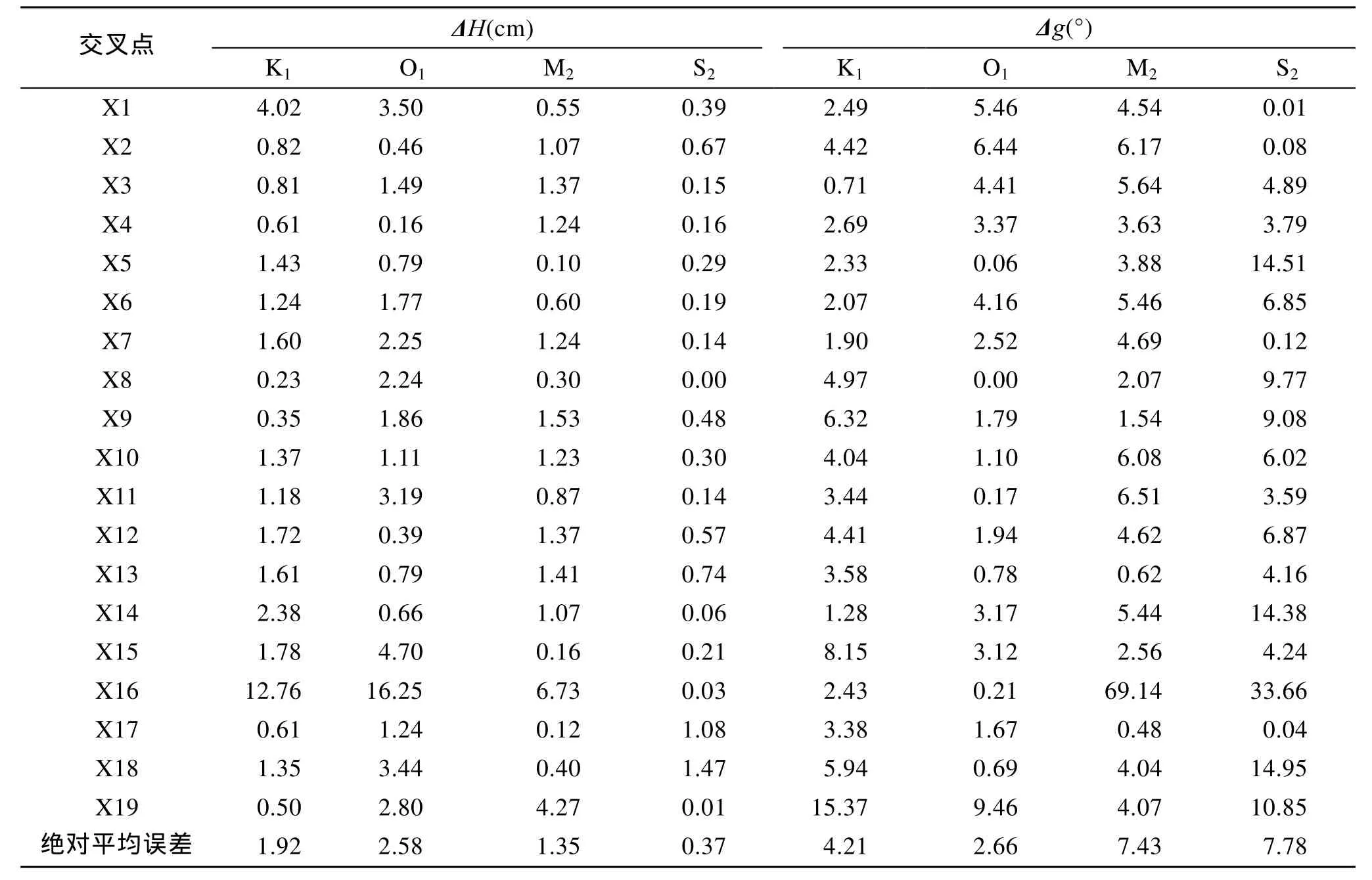
表5 TPXO7.2结果与j, v模型计算结果的比较Tab. 5 Comparison between the results of TPXO7.2 and j, v model

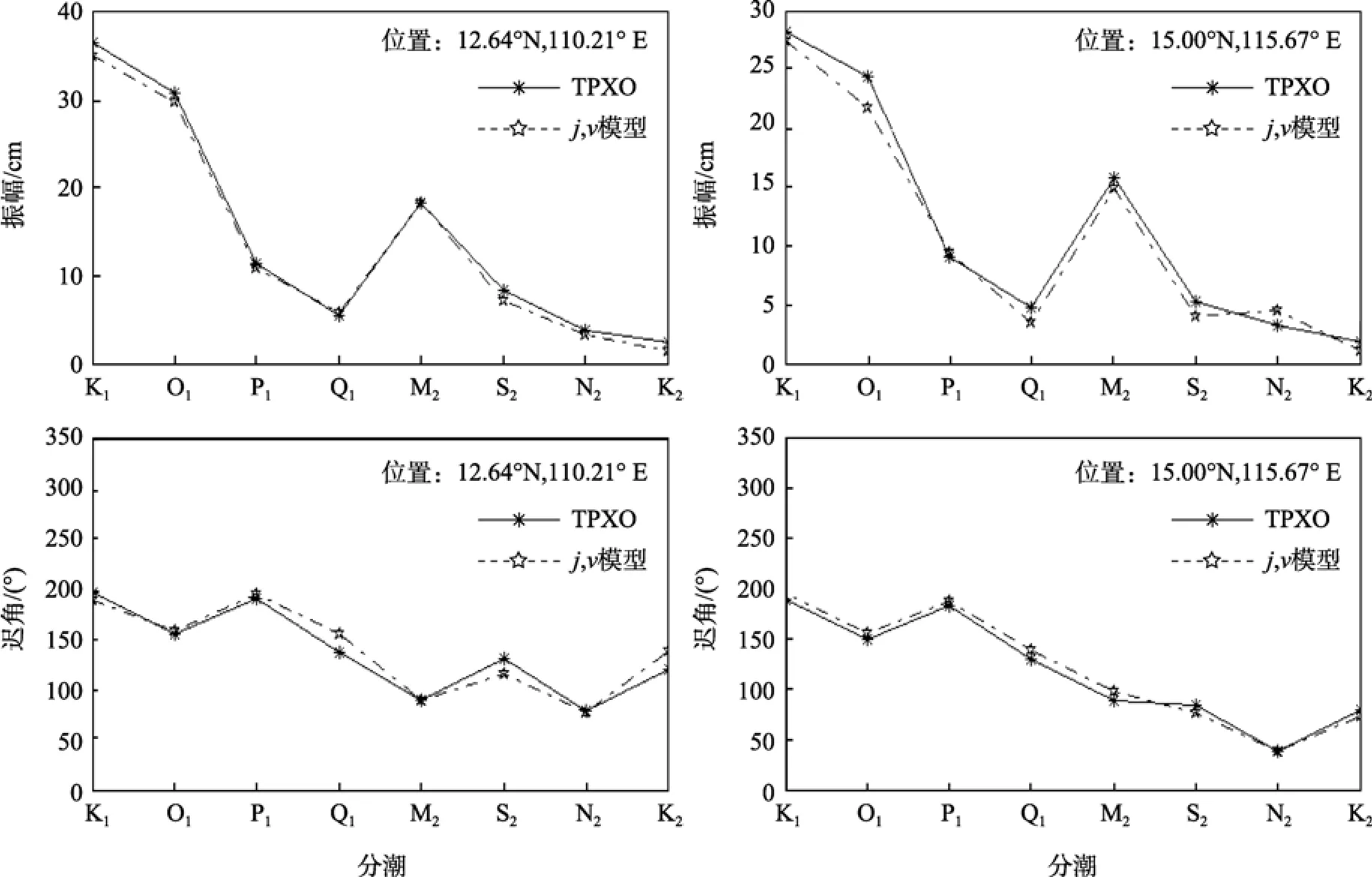
图2 任选的两个位置的TPXO7.2结果与j, v模型计算结果的比较Fig. 2 Comparison between the results of TPXO7.2 and j, v model at two random points

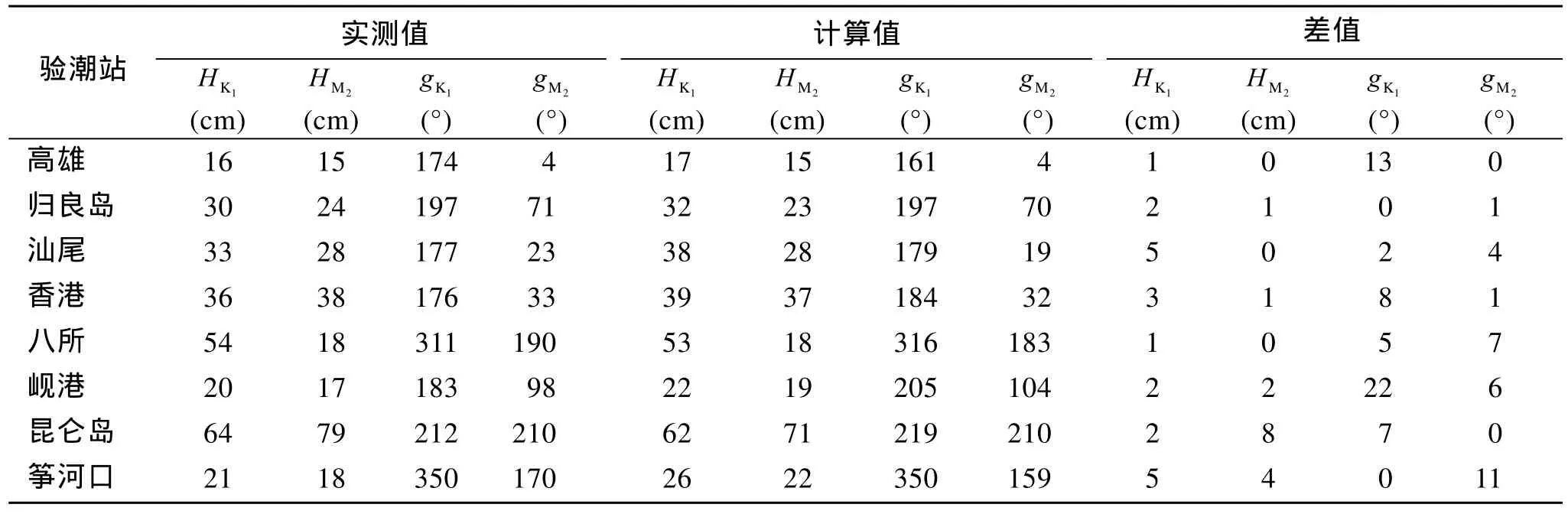
表6 j, v模型计算结果与沿岸验潮站实测结果的比较Tab. 6 Comparison between j, v model results and ground-measured harmonics at the tidal stations

3.4 K1, O1, M2和S2的同潮图

根据j,v模型, 利用卫星高度计资料可计算出南海研究区域各个分潮的调和常数, 获取了 T/P卫星每个星下点处 8个主要分潮的调和常数, 通过插值,给出了南海区域K1, O1, M2和S2的同潮图(图3)。

由图 3可见, 南海的潮汐以全日潮为主, 四个主要分潮均由吕宋海峡传入南海并向西南传播, 其振幅从吕宋海峡向西南方向增大。四个分潮在深海区的传播速度较快, 等值线稀疏, 它的位相变化比较慢, 粗略估计它在深海区的传播速度约为 800 km/h, 这与水深为4 000 m左右的重力波的传播速度非常接近。相比而言, 它在北部湾里面的传播速度要慢得多。

除东北部吕宋海峡及其西南区域外, 南海大部分区域K1分潮的振幅都大于30 cm。在北部湾K1分潮的振幅要显著地大于其他海区, 最大振幅接近80 cm, 湄公河入海口处的K1分潮的振幅也达到了70 cm。O1相对 K1分潮较小一些, 在南海大部分区域振幅都也在30 cm左右, 北部湾里面O1分潮的最大振幅达到90 cm, 湄公河入海口处的O1分潮的振幅有40 cm。相对于全日潮, 南海大部分海区的半日潮影响较小,但其传播较为复杂, 振幅变化也不显著, 大小约为15 cm, 台湾海峡和湄公河的入海口附近 M2分潮的振幅要显著地大于其他海区, 最大振幅超过90 cm。北部湾里面M2分潮的振幅在20 cm左右, 同样可以看出, S2分潮在南海的振幅较小, 大部分海区小于10 cm, 只在台湾海峡和湄公河的入海口处比较大,大于30 cm。

与现有的海洋水文图集[21]中南海潮汐的同潮图比较可见: 南海中部海区分潮的振幅、迟角符合较好;由卫星测高得出的潮汐同潮图中, 北部湾南部顺化附近退化的 K1分潮无潮点没有很好地显示出来, 台湾海峡附近潮波系统复杂, 卫星测高得出的M2分潮的振幅略小, 从这两处可以看出, 应用卫星高度计资料处理近海潮汐问题还有待进一步深入和研究。在外海深水区, 常规观测点较少, 且连续观测时间短, 而卫星观测点多, 且精度较高; 近岸常规观测点较多, 且精度较高, 而卫星观测点较疏, 测高误差也较大。由此可见, 若将两种资料结合起来将可获得高精度潮汐分布特征。

4 结论

利用高度计资料研究海洋时, 由于T/ P卫星采样的时间间隔大而造成了潮汐的高频混淆, 混淆的频率同分潮的本身频率和卫星采样间隔有关, 本文采用了卫星高度计 10 a的测高数据, 有效减小了分潮的高频混淆。利用j,v模型调和分析方法提取了南海 8个主要分潮潮汐调和常数。交叉点处上下行轨道的 8个主要分潮的向量均方根偏差均小于 3 cm;与TPXO7.2模式结果比较, 交叉点处K1, O1, M2和S2的振幅绝对平均误差均不超过 3 cm, 迟角的绝对平均误差均不超过 8°; 与选取的 8个验潮站实测结果比较, 其向量均方根偏差不超过 5 cm。通过以上的比较, 均验证了利用j,v模型调和方法在南海进行卫星高度计资料潮汐信息提取的可靠性。给出的4个主要分潮同潮图对南海潮波系统的研究提供了较可靠的资料依据, 并可为局部重力场的研究提供海洋潮汐改正数据, 有一定的参考价值。

图3 主要分潮的同潮图Fig. 3 Cotidal chart for four principal constituents

[1] Mazzega P, Berge M. Ocean tides in Asian semienclosed seas from TOPEX/Poseidon [J]. Journal of Geophysical Research, 1994, 81: 3201-3210.

[2] Morimoto A, Yanagi T, Kandko A. Tidal correction of altimetry data in the Japan Sea [J]. J Oceanogr, 2000,56: 31-41.

[3] 李立, 吴日升, 李燕初, 等. TOPEX/POSEIDON高度计浅海潮汐混淆的初步分析[J]. 海洋学报, 1999,21(3): 1 -14.

[4] 董晓军, 马继瑞, 黄城, 等. 利用 TOPEX/POSEIDON卫星高度计资料提取东中国海潮汐信息的研究[J]. 海洋与湖沼, 2002, 33(1): 7-13.

[5] 李燕初, 蔡文理, 李立, 等. 由TOPEXPOSEIDON卫星高度计资料导出福建和台湾邻近海域的潮汐特征[J]. 海洋学报, 2002, 24(1): 154-162.

[6] Fang G H, Wang Y G, Wei Z X, et al. Empirical cotidal charts of the Bohai, Yellow and East China Seas from 10 years of TOPEX/POSEIDON altimetry [J]. Journal of Geophysical Research, 2004, 109(C11006), doi:10.1029/2004JC002484, 2004.

[7] Yanagi T, Morimoto A, Ichikawa K. Co-tidal and co-range charts for the East China Sea and the Yellow Sea derived from satellite altimetric data [J]. J Oceanogr, 1997, 53: 303- 309.

[8] Yanagi T, Takao T, Morimoto A. Co-tidal and co-range charts in the South China Sea derived from satellite altimetry data [J]. La Mer, 1997, 35: 85-93.

[9] Fang G H, Kwok Y K, Yu K J, et al. Numerical simulation of principal tidal constituents in the South China Sea, Gulf of Tonkin and Gulf of Thailand [M]. Continental Shelf Research 1999, 19: 845-869.

[10] 暴景阳, 晁定波, 李建成. 南中国海 TOPEX/POSEIDON轨迹交叉点测高数据的潮汐调和分析[J].测绘学报, 2000, 29(1): 17-23.

[11] 毛庆文, 施平, 齐义泉. 运用调和分析方法分离卫星高度计资料中的潮汐信息[J]. 海洋工程, 2002, 20(1):41-45.

[12] 李培良, 左军成, 李磊,等. 南海 TOPEX/POSEIDON高度计资料的正交响应法潮汐分析[J]. 海洋与湖沼,2002, 33(3): 287-295.

[13] 吴自库, 田纪伟, 吕咸青,等. 南海潮汐的伴随同化数值模拟[J]. 海洋与湖沼, 2003, 34(1): 101-108.

[14] Tian J W, Zhou L, Zhang X Q, et al. Estimates of M2 internal tide energy fluxes along the margin of Northwestern Pacific using TOPEX/POSEIDON altimeter data [J]. Geophysical Research Letters, 2003, 30(17):1889-1889.

[15] 汪一航. 卫星高度计资料在海洋潮汐研究中的应用[D]. 青岛: 中国科学院海洋研究所, 2008.

[16] 方国洪, 郑文振, 陈宗镛,等. 潮汐和潮流的分析和预报[M]. 北京: 海洋出版社, 1986: 67-88.

[17] Horn W. Tables of astronomical arguments Vo+v and corrections j, v for use in the harmonic analysis and prediction of tides for the years 1900 to 1999. Proceedings of the symposium on tides organized by the Int[J]. Hydrogr Burean Monaco, 1969, 12: 167-168.

[18] 陈宗镛. 潮汐分析和推算的一种j, v模型[J]. 海洋学报, 1990, 12(6): 693-703.

[19] Desai S D, Wahr J M. Empirical ocean tide models estimated from TOPEX/POSEIDON altimetry [J]. Journal of Geophysical Research, 1995, 100: 25205-25228.

[20] Egbert G D, Erofeeva S Y. Efficient inverse modeling of barotropic ocean tides[J]. Journal of Atmospheric and Oceanic Technology, 2002, 19(2): 183-204.

[21] 海洋水文图集编辑委员会. 南海海洋图集(水文) [M].北京: 海洋出版社, 2006: 314-317.

The South China Sea tides analysis based on TOPEX/Poseidon altimetry

ZHAO Yun-xia1,2, WEI Ze-xun1,2, Wang Xin-yi1,2
(1. Key Laboratory of Marine Science and Numerical Modeling, State Oceanic Administration, Qingdao 266061,China; 2. The First Institute of Oceanography, State Oceanic Administration, Qingdao 266061, China)

May,4,2011

tides; the South China Sea; TOPEX/Poseidon; j, v model

Harmonic analysis of 10 years (1992~2002) of TOPEX/Poseidon (T/P) along-track altimetry is performed to derive the semidiurnal (M2, S2, N2and K2), diurnal (K1, O1, P1and Q1) tides in the South China Sea. The T/P solutions are evaluated through intercomparison for 19 crossover points, comparison with the results of TPXO7.2 and the ground truth, showing that the vector root mean square errors at crossover points of M2, S2, K1and O1are 1.53, 1.15, 2.57 and 1.41cm, respectively and the absolute mean error with TPXO7.2 is less than 3 cm in amplitudes and 7° in phase lags for principal constituents (M2, S2, K1and O1), and the RMS errors from comparing with the ground truth are less than 5 cm. All above show that the accuracy of j, v model harmonic analysis of T/P altimeter data in the South China Sea is reliable.

P731.2

A

1000-3096(2012)05-0010-08

2011-05-04;

2012-03-05

国家高技术研究发展计划(863计划)重点课题(2008AA09A401-05)

赵云霞(1987-), 女, 黑龙江牡丹江人, 硕士研究生, 主要从事物理海洋研究, 电话: 15092201516, E-mail: zhaoyx@fio.org.cn;魏泽勋, 通信作者, 男, 研究员, 主要从事海洋环流、数值模拟和资料同化的研究, E-mail: weizx@fio.org.cn

(本文编辑：刘珊珊)