珩磨机运动控制卡的三次B样条曲线插补算法*

张万军 胡赤兵 张 峰 张国华 龚 俊

（①兰州理工大学数字制造技术与应用省部共建教育部重点实验室，甘肃兰州730050;②兰州理工大学机电工程学院，甘肃兰州730050;

③兰州工业化设备有限公司，甘肃兰州 730050）

在数控珩磨机加工中，经常会遇到如飞机机翼、飞机叶轮等许多具有复杂外形轮廓的零件。在传统数控加工中加工这些不规则曲线的零件时，加工程序只能通过离线方式CAD/CAM方式下编程来完成，这就使得加工速度受到严重限制。因此研究数控系统曲线的新的插补方法显得尤为重要［1］。

三次B样条曲线是在数控加工领域中应用较多的样条曲线，它可以用来描述复杂曲线曲面的零件轮廓。数控珩磨机运动控制系统中通常用TMS320F2812芯片的结构专门为实时信号处理而设计，集实时处理能力和控制外设能力于一身，处理功能强大，使用各种伺服控制系统。本文介绍将三次B样条曲线与DSP运动控制卡技术相结合的实时插补方法，该方法克服了传统轨迹插补方法的缺点，有效地简化了插补过程中的轨迹计算，提高了运算速度和控制精度［2］。

1 三次B样条曲线实时插补

1.1 三次B样条曲线的数学表示

在三维空间中有如下关系［3］:

式中:u为参变量数（u∈［0，1］），Ai为为一组系数矢量。

1.2 三次B样条曲线的实时插补

设V为沿曲线的进给速度，可由曲线对时间t求导得到［4－5，7］:

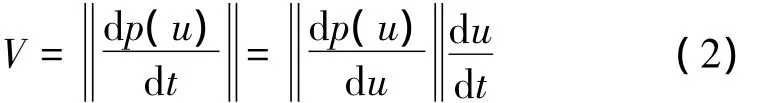
因此，u对t的一阶导数可以表示为

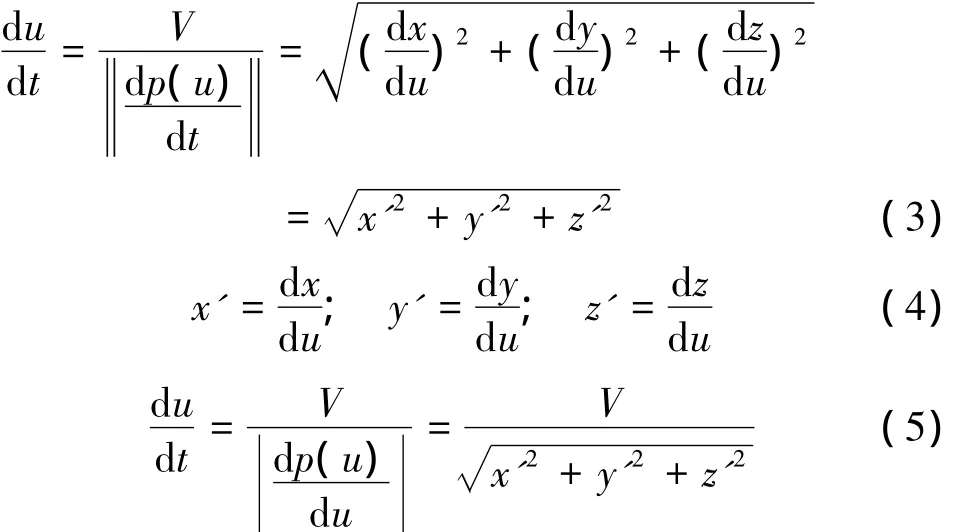
所以，一阶展开式的近似计算公式为

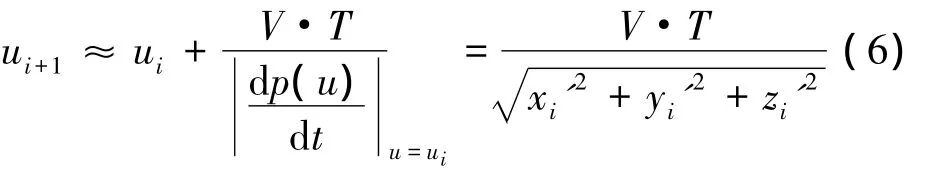
当插补周期T→0时，ui+1≈ui，可以满足泰勒公式一阶展开式插补近似迭代。如果曲线曲率半径很小，便于可以满足泰勒公式二阶展开式插补近似迭代:

式（6）、（7）中，当前ui+1与ui（xi，yi，zi）对泰勒公式求一阶导数、两阶导数，得到（xi+1，yi+1，zi+1）的坐标点。

1.3 三次B样条曲线的插补弓高误差分析

由于三次B样条曲线实时插补，在每一个插补点上不存在误差，主要是弓高误差影响了插补精度。弓高误差指的是一段曲线上连接两端点的弦与弧的最大法向差［3］。如图1所示:2个插补点分别为p（ti）和p（ti+1），径向误差为e可用e≈MN来表示，求得p（ti）和p（ti+1）的坐标位置。令|p（ti）p（ti+1）|=V·T代入式（1）中得

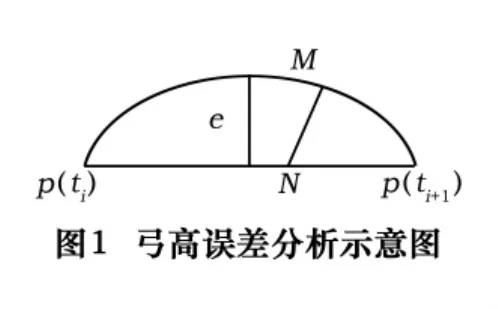
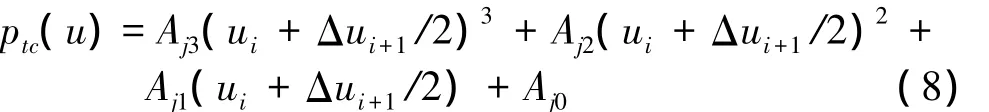
1.4 三次B样条曲线的插补算法流程图

笔者针对上面插补算法的过程分析，给出了该插补算法的插补流程图，如图2所示。

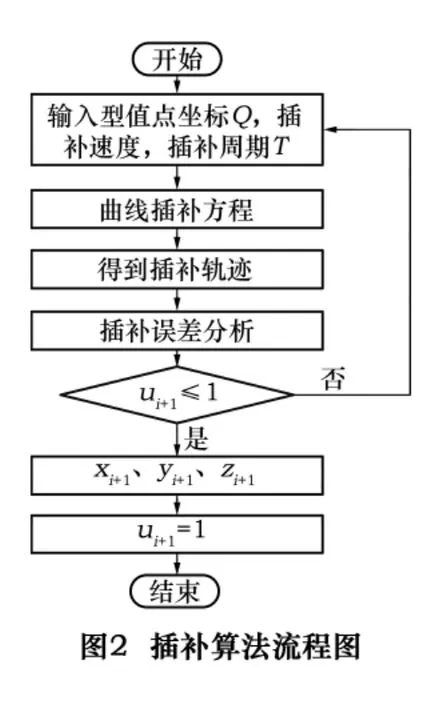
2 利用DSP运动控制卡实时插补

本文采用的DSP运动控制卡数控珩磨机运动控制结构图如图3所示，USB和RAM具有通讯和存储的功能，主要是以 TMS320F2812为核心控制，DSP控制速度达到40MIPS的速度，总线扩展通过CF卡来实现［6］。定时器T1、T2、T3发出的脉冲数来完成脉冲控制，通过控制运动控制卡定时器来调整插补轨迹，保证了3个驱动轴能同时到达预先的位置，实现3个驱动轴的空间插补，达到了高速高精度插补的要求。运动控制发出的信号通常为“脉冲（CP）+方向（DIR）”的形式，该运动控制器输出三组脉冲/方向信号，实现数控系统的速度和位置控制［1］。

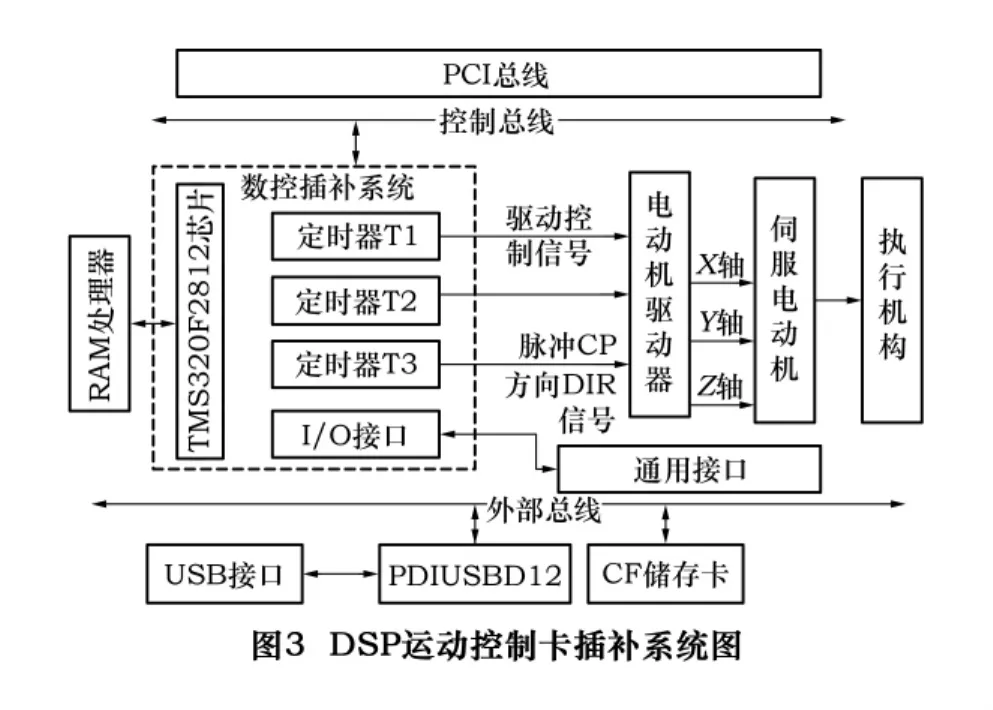
在TMS320F2812 DSP运动控制卡上进行实际控制时，每一台电动机轴驱动器需要控制2个信号，一个脉冲CP信号和另外一个方向DIR信号。于是本文选用如图3所示的DSP运动控制卡作为插补的数控系统，保证控制每一个轴的实际运动位置。应用这种插补方法，在插补器上进行调试，得到了预期的插补效果。下面主要介绍这种插补算法在硬件系统中实现的思想。

控制脉冲的发送是通过定时器T1、T2、T3中断来完成，设一个周期内x轴、y轴、z轴的实际脉冲数为nnx、nny和nnz，令CPx=T/nnx，CPy=T/nny和CPz=T/nnz，则每一个脉冲的时间的坐标为{CPx，2CPx，3CPx，…，T}和{CPy，2CPy，3CPy，…，T}{CPz，2CPz，3CPz，…，T}。将 min{CPx，CPy，CPz}的值存储在寄存器中，在定时器中发射脉冲数，向3个轴的方向移动坐标的位移。中断查询3个轴的脉冲数，使x轴、y轴和z轴的脉冲坐标相等完成查询插补。

本文提出的插补算法是以x轴、y轴和z轴某一轴脉冲频率为基准，使该轴发出的脉冲数与定时器中断严格同步，也让其他两轴同步运动，从而尽可能保证了插补轨迹是一条空间曲线的运动轨迹。

3 插补实例

根据三次B样条曲线实时插补算法，文章给出了空间三次B样条曲线插补的实例。输入型值点Q1=［0.636 0.742 11］，Q2=［0，0，1］，Q3=［25，30，6］，Q4=［50，50，16］;进给速度v=10 mm/s;插补周期T=0.01 mm。所确定的一段三次B样条曲线插补的轨迹如图4所示，是一条空间曲线完全符合插补运动的控制要求。

4 结语

三次B样条曲线理论曲线和实际曲线发出脉冲数相等，无弓高等累计误差从而说明理论曲线和实际曲线相吻合，验证了该算法的正确性和合理性。该算法实现三轴的联动插补，拓展了从平面到空间的插补。在DSP运动控制卡上实时插补能够大大提高运算速度和运算准确性，也能够提高加工精度和加工效率，在其他数控插补的过程中具有借鉴意义。

［1］王婕，王宝仁，张承瑞.基于DSP的嵌入式运动控制器插补算法及误差补偿研究［J］.组合机床与自动化加工技术，2007（6）:8－11.

［2］李广涛，薛重德，侯小强.基于TMS320F2812的三次B样条曲线实时插补［J］.中国制造业信息化，2008，12（23）:55－57.

［3］叶伯生，杨叔子.CNC系统三次B样条曲线的高速插补方法的研究［J］.中国机械工程，1998，9（3）:42－－44.

［4］高钟旈.机电控制工程［M］.2版.北京:清华大学出版社，2002.

［5］施法中.计算机辅助几何设计与非均匀有理B样条［M］.北京:高等教育出版社，2001.

［6］苏奎峰，吕强，靳岚，等.TMS320X281X DSP原理及 C程序开发［M］.北京:北京航天航空大学出版社，2008.

［7］Feng Jingchun，Li Yuhao，Wang Yuhan，et al.Design of a real－time adaptive NURBS interpolator with axis acceleration limit［J］.Int J Adv Manuf Technol，2010，48（1－4）:227－241.