基于NURBS最小二乘逼近的微段平滑加工算法*

沈 斌 齐党进 樊留群② 朱志浩②

（①同济大学中德学院，上海200092;②同济大学沈阳机床研究院，上海 201804）

微小直线段离散化曲线加工路径的微段加工方式仍被广泛地应用。而在该加工方式下，通常是借助CAM软件，由后置处理将连续加工路径离散化为大量的微小直线段，生成数控程序文件并输入到数控机床，然后数控系统根据由微小直线段组成的折线进行插补和加工。微段加工方式下加工程序量过大和需要频繁加减速来满足加工精度要求的不足饱受诟病。为了实现微小直线段的高速平滑加工，提高加工效率，国内外学者作了大量的研究工作，其中，部分研究成果已经被应用到国外的高档数控系统中，例如:西门子Sinumerik 840D中的压缩功能（COMPOF/ON，COMPCURV，COMPCAD），Fanuc的 FS 30i/31i/32i中的纳米平滑（Nano Smooting）功能。

按优化的方式不同，研究可以大致分为两个方向:微段拐点处的速度平滑和基于微段拟合的自由曲线直接插补。其中，前者的研究较早也较多。徐志明等［1］，以前瞻得到的夹角和微段长度为计算前提，用递归算法求解微段转接点处的最大允许进给速度;王宇晗等［2］提出了微小线段速度衔接的数学模型并基于此求得进给速度限制的近似最优解，然后以直线加减速方法进行速度规划，许海峰等［3］进一步对该数学模型进行了离散化并加以完善，给出了离散化下的速度限制值计算方法，并以削峰填谷的方法处理新路径与原始路径之间的长度差异;彭芳瑜等［4］进一步考虑了机床的动力学约束;黄昕等［5］提出了一种以最大进给速度为目标，通过双向扫描算法，获得拐点处的最优进给速度的算法，并以S形加减速控制方法进行速度规划，实现了微段平滑加工;叶伟［6］和李小清［7］也根据各自的微小段加工速度、加速度衔接模型，并以S形加减速方法进行了速度规划;冷洪滨等［8］除了对合成速度进行限制外，进一步对单轴的运动速度进行限制，并以三次多项式加减速方法进行了速度规划。与上面的方式不同，杨开明等［9］为代表，通过在相邻程序段间加入过渡段，以牺牲局部精度的前提下避免微段拐点处减速而实现速度的平滑。

虽然以上微段优化方式可以提高加工效率和加工精度，但是，伴随着加工速度的进一步提高，为了满足加工精度的要求，微小直线段变得越来越短，上述优化方式必然造成计算量过大，致使加工等待等问题。为此，拟合的自由曲线直接插补优化方式相应提出。该优化方式是将微小直线段用多项式曲线、三次样条和B样条等进行拟合，然后进行直接插补。其中，Erkorkmaz［10］和 Yau 等［11］以弦长为参数，分别采用五次样条曲线和Bézier曲线来拟合微小直线段从而生成新的光滑加工路径来解决微段加工出现的问题;任锟等［12］对离散加工路径采用三次样条曲线拟合，然后分析三次样条发现高曲率点，预估高曲率点处的最优速度，并通过S形加减速控制实现微段优化加工;张园等［13］以弦长为参数，采用五次样条曲线拟合微小直线段生成新的光滑加工路径，并附加考虑了弓高误差的限定对整个样条拟合曲线进行速度规划，实现了进给速度的自适应控制。

因此，针对微段加工中出现的不足，本文提出了基于NURBS最小二乘逼近的微段平滑加工算法来实现微小直线段的平滑加工，即将离散的刀位点数据拟合成一条NURBS曲线作为新的加工路径，然后可以按照新的加工路径进行NURBS实时插补，实现微小直线段的平滑加工。

1 基本思想和算法流程

基于NURBS最小二乘逼近的微段平滑加工算法的基本思想是，对从微段加工程序解析得到的刀位点进行自适应分区拟合。如流程图（图1）所示，首先进行一定段数的预读，然后根据给定的限制条件将微段自适应分为各个区域，最后对符合拟合条件的区域逐区进行带权因子和一阶导数约束的最小二乘NURBS曲线逼近，并进行NURBS曲线实时插补，而对其他部分划分为直线段区域，使用直线插补方式。

2 自适应分区

通过对微小直线段一定段数的预读可以得到以下两个基本信息:相邻微段间的夹角θi和微段的长度Li（i=0，1，2，…）;又考虑到拟合的时间与被拟合的点数相关，因此，自适应分区受3类条件限制:拟合最大刀位点数限制，微段间夹角有关限制和微段长度有关限制。根据限制条件，将微小直线段自适应划分为不同的区域，并定义限制条件临界处的刀位点为断点，作为上一区域的终点和下一区域的起点。

2.1 最大刀位点数限制nlim

鉴于微段一般短且多的特色，最大刀位点数限制作为自适应分区的首要限制条件。nlim的大小与数控系统控制器的运算能力和对实时性的要求（插补周期T）有关系。当两个断点间的累加数据点数n≥nlim时，当前刀位点Pi作为断点，断点前的n+1个刀位点划为一个适合拟合区域。

2.2 微段夹角有关限制

θlim为最大夹角限制，可以根据给定进给速度F、最大加速度Amax和插补周期T估算得到，即

当 θi＞θlim时，Pi为一尖点，则将Pi－2到Pi+2的四个微小直线段划分为直线段区，Pi－2为断点，Pi+2为下一区域的起点;

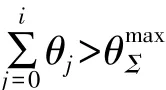
2.3 微段长度有关限制

微段长度作为自适应分区的辅助限制。当微段长度很短，特别是接近1～2个插补长度时，对其进行拟合运算并不能使加工平滑，只会增加拟合计算的时间，影响实时性;与此类似，当微段长度很长时，在增加拟合时间的同时，拟合运算反而会使该直线段加工精度变差。在多类型曲线的拟合仿真中，反复验证了以上结论。因此，微段长度限制分别对最短微段长度Lmin和最长微段长度Lmax进行限制。当Lmin≤Li≤Lmax时，该刀位点被划入当前适合拟合区域，并读入下一个刀位点，否则微段PiPi+1划为直线段区域，Pi作为断点（适合区域的终点），Pi+1作为新的区域的起点。默认取Lmin=FT;Lmax=100FT。

3 带权因子和一阶导数约束的NURBS曲线最小二乘逼近算法

带权因子和一阶导数约束的NURBS曲线最小二乘逼近算法的基础是最小二次逼近法。考虑到适合拟合区域的局部数据点拟合误差较大（拟合误差大于给定最大误差值）和进给速度方向的限制，本文提出的算法在NURBS曲线最小二乘逼近算法的基础上，对拟合误差较大的点增加了权因子约束，对进给速度方向限制（法向矢量给出）的点增加一阶导数约束，使拟合得到曲线更接近原始加工路径。

3.1 算法流程

如图2所示，带约束NURBS最小二乘逼近基本流程为:首先按照修正弦长法对读入的数据点进行参数化，然后根据各点的权因子和一阶导数约束进行最小二乘拟合，得到最大逼近误差范围内的控制点，生成新的NURBS曲线加工路径。

假设适合拟合的r+1个数据点为qi（i=0，1，…，r），qi受权因子hi（hi≥1）或一阶导数fi（进给速度方向）的约束，拟合得到的 NURBS曲线为C（u）（u∈［ui，ui+1］⊂［u3，un+1］）［14］。

3.2 数据点的参数化［14］

在采用NURBS曲线对适合拟合区域进行逼近以前，必须对数据点进行参数化，即为每一个数据点赋予一个参数值。常用的参数化方法包括均匀参数化、弦长参数化、向心参数化和修正弦长参数化等。为了满足拟合曲线的光顺性要求，本算法采用修正弦长参数法。假设适合拟合区域包含r+1个刀位点数据，记为点集{qi}（i=0，1，2，…，r），对应的参数为{ui}，按照修正弦长参数法可得各数据点的参数:

式中:ki为修正弦长系数

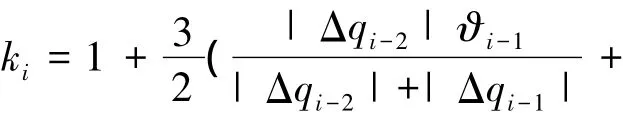
修正系数ki≥1，用于修正弦长偏短且前后相邻夹角偏大的数据点，使拟合后的曲线在该点处的曲率相应较大，且向心加速度可以平稳变换。ki的大小取决于与数据点前后的弦长和夹角的关系。

简言之，若|Δqi－1|相比前后相邻的弦长 |Δqi－2|和|Δqi|越小，且前后相邻弦线夹角的外角 ϑi－1和 ϑi（不超过π/2时）越大，ki也越大，对应于曲线段绝对曲率偏大。当ϑi－1=ϑi=π/2时，修正系数ki将达到最大值。

3.3 获取权因子hi

默认权因子hi=1（可以通过手工编程指定，则hi=编程值），当数据点qi最小二乘数逼近误差εi超出给定最大逼近误差εmax时，增大该点处的权因子（hi=chhi，ch为权因子修正系数，默认ch=5），然后重新迭代计算，直到满足 εi≤εmax。

3.4 获取一阶导数fi

首末端点的一阶导数f0和fr可以根据给定的首末端点边界条件计算得到，例如:q0处的边界条件为切矢条件时，f0为上一段加工程序在q0处的切矢。中间点的一阶导数按照下列规则得到:若未给定，则该数据点为非约束点;若手工编程指定，则fi为编程值;若已给定法向矢量，则fi通过法向矢量近似计算，近似计算方法如下:

假设法向矢量为ni，qiqi+1为点qi到qi+1的矢量，fi可近似计算得

其中，α为qiqi+1与ni的夹角，

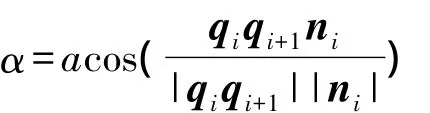
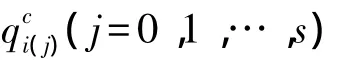
并进一步令

D=［d0，d1，…，dm］T，一个包含m+1 个控制点（d1=（xi，yi，zi），l=0，1，…，m）的矩阵;

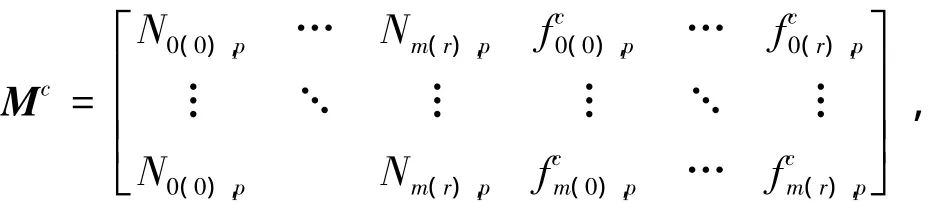
一个包含约束点p次基函数和对应p次的（r+1）×（m+1）维矩阵;

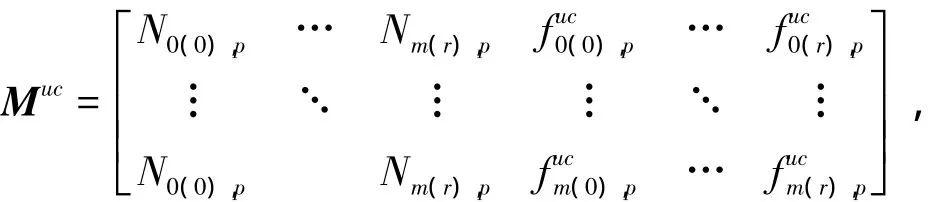
一个包含非约束点p次基函数和对应p次（l=0，1，…，m）的（r+1）×（m+1）维矩阵;

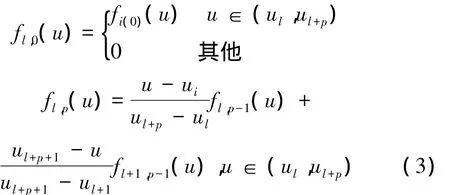
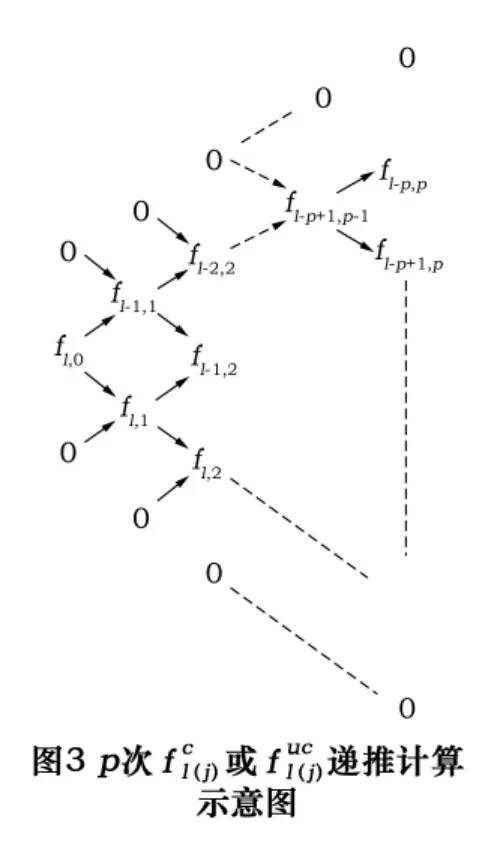
与p次基函数的求法一致，如图3，式（2）也可以根据de Boor－Cox递推算法求得。

3.5 算法描述

带约束的NURBS曲线最小二乘逼近算法的基本思想是拉格朗日乘数法，即引入2（s+1）个拉格朗日乘数因子，解一个系数矩阵为（2s+m+3）维方阵的线性方程组。

设拉格朗日乘数因子为λk（k=0，1，…，2s+m+3），令A=［λ0，λ1，…，λ2s+m+3］，可得

非约束点满足方程

约束点满足方程

根据拉格朗日乘数法，应使式（6）达到最小。

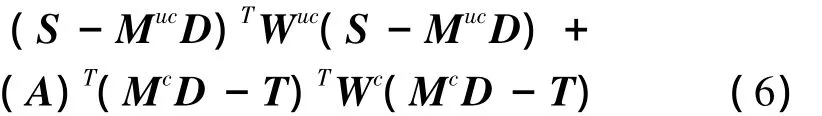
分别对A和D求导，并令其等于0，可得

对式（7）进行变形，可得

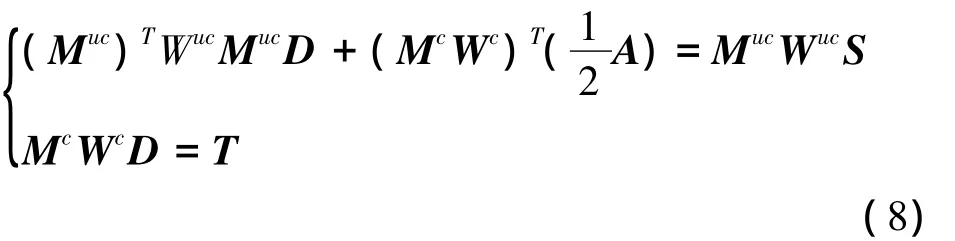
令A/2仍为A，并表示为矩阵形式，可得

根据式（9），可解得

代入式（9）第二式，进一步可推得

解得

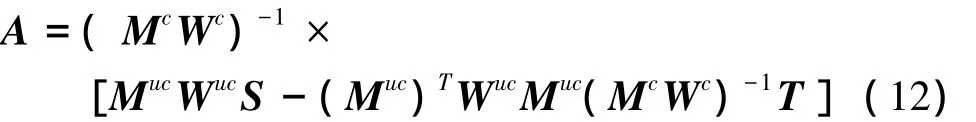
通过式（12）可以接到拉格朗日乘数因子矩阵A，代入式（11），即可解得所需的控制点D，得到所需的p次NURBS曲线。

4 仿真与实验

为了验证算法的正确性和有效性，对原始图形为三瓣花的微段加工路径进行仿真与测试。其中，相关限制参数为:最大数据点数nlim=30;微段长度（Lmin，Lmax）为（0.02，20）;最大夹角 θlim=π/9;最大夹角差Δθlim=π/18;最大夹角累加值=π/2;给定最大逼近误差εmax=0.002 mm。通过利用Matlab进行仿真验证，可得微段加工路径NURBS曲线最小二乘逼近的仿真结果（图4）。分析图4b可知，三瓣花逼近的实际最大误差为3.24×10－3mm，均小于给定的最大逼近误差值。

5 结语

为了消除微小直线段加工方式下加工程序量过大和需要频繁加减速的诟病，实现微小直线段的高速平滑加工，提高加工效率，本文提出了带权因子和一阶导数约束的NURBS曲线最小二乘逼近算法，将离散的数据点拟合成一条NURBS曲线，给出了算法的应用流程，经过初步验证，可以实现微小直线段的平滑加工。

［1］徐志明，冯正进，汪永生，等.连续微小路径段的高速自适应前瞻插补算法［J］.制造技术与机床，2003（12）:20－23.

［2］王宇眙，肖凌剑，曾水生.小线段高速加工速度衔接数学模型［J］.上海交通大学学报，2004，38（6）:901－904.

［3］许海峰，王宇晗，李宇昊，等.小线段高速加工的速度模型研究和实现［J］.机械工程师，2005（4）:9－13.

［4］彭芳瑜，李黎，陈徐兵.连续小直线段高速高精插补中的动力学约束条件［J］.计算机辅助设计与图形学学报，2006，18（12）:1812－1816.

［5］黄昕，李迪，李方，等.基于双向扫描算法的小线段速度规划［J］.计算机集成制造系统，2009，15（11）:2188－2192.

［6］叶伟，王小椿.一种连续小线段高速插补算法［J］.南京理工大学学报:自然科学版，2008，32（4）:443－448.

［7］李小清，朱凯.数控加工小线段高速平滑衔接插补算法［J］.组合机床与自动化加工技术，2010（9）:1－5.

［8］冷洪滨，邬义杰，潘晓弘.三次多项式微段高速加工速度规划算法研究［J］.计算机集成制造系统，2008，14（2）:336－340.

［9］杨开明，石川，叶佩青，等.数控系统轨迹段光滑转接控制算法［J］.清华大学学报:自然科学版，2007，47（8）:1295－1299.

［10］Erkorkmaz K，Altintas Y.High speed CNC system design.Part I:jerk limited trajectory generation and quintic spline interpolation［J］.International Journal of Machine Tools and Manufacture，2001，41（9）:1323－1345.

［11］Yau H T，Wang J B，Chen W C.Development and implementation for real－time look ahead interpolator by using Bezier curve to fit CNC continuous short blocks［C］.In:2005 IEEE International Conference on Mechatronics.NJ，USA:IEEE，2005:78－83.

［12］任锟，傅建中，陈子辰.高速加工中速度前瞻控制新算法研究［J］.浙江大学学报:工学版，2006，40（11）:1985－1988.

［13］张园，陈友东，黄荣瑛，等.高速加工中连续微小线段的前瞻自适应插补算法［J］.机床与液压，2008，36（6）:1－4.

［14］Piegl L，Tiller W.非均匀有理B样条［M］.2版.北京:清华大学出版社，2010.