面对面垂直度误差的数据处理*

周景亮 林志熙

（福建工程学院机电及自动化工程系，福建福州 350108）

面对面垂直度误差检测是机械加工测量中经常遇到的问题。传统的测量方法（如直角尺看光隙、直角尺配塞尺、简易打表法等）由于不符合面对面垂直度误差的定义，存在着原理误差，因而不能准确地得到面对面垂直度误差值，只能用于检验位置精度要求较低的工件，且调整、测量效率低;而三坐标测量机成本高，不适合车间现场检测。

因此，本文采用万能工具显微镜对被测工件进行坐标测量，建立基准符合最小条件法、最小二乘法、三远点法和对角线法的面对面垂直度误差评定的数学模型，利用数学软件MATLAB进行快速有效的计算处理，获得准确的面对面垂直度误差值及误差示意图，求解数据的可视化效果大大强于三坐标机的图示化效果。最后通过测量示例证明本文提出的方法具有较高的评定精度和较好的实用性。

1 数学模型

GB/T 1958—2004规定:定向最小区域是指按拟合要素的方向包容被测提取要素时，具有最小宽度f或直径Φf的包容区域［1］。因此，在评定面对面垂直度误差时，首先要确定基准拟合要素的方向，即对基准提取要素的平面度误差进行评定。然后垂直于基准拟合要素的方向，寻找包容被测提取要素时，具有最小宽度的定向最小包容区域。

1.1 基准平面的建立

建立基准平面，即对基准提取要素进行平面度误差的评定。常用的有最小区域法、最小二乘法、三远点法和对角线法。其中最小包容区域法是国家标准规定的方法，采用最小包容区域法评定时产生的误差最小，精确度最高。

1.1.1 最小区域法

根据参考文献［1］规定，按最小区域法评定平面度误差实质上是寻找包容基准提取要素且距离最短的两平行平面。如图1所示零件并建立坐标系。基准平面的一般方程可简写为:A1x+B1y+C1z=1，设基准面上任一测量点坐标为Pi（xi，yi，zi）（i=1，2，…，n），测点到基准平面的距离为

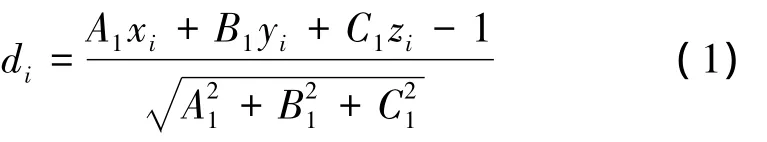
最小区域法的目标函数F（A1，B1，C1）=［di］max－［di］min，满足最小化时，F（A1，B1，C1）的（A1，B1，C1）即基准平面的法向量，且该三元函数F（A1，B1，C1）的最小值即为平面度误差。因此基准平面的评定就转化为求三元函数F（A1，B1，C1）的最小值问题。

1.1.2 最小二乘法

1.1.3 三远点法

三远点法是按被测实际表面上相距最远的3点建立基准平面，以各测点对此平面的偏差中最大值与最小值的代数差作为被测实际表面的平面度误差值。只要选定三远点，根据平面点法式方程，即可求得基准平面的法向量。由于测量点的选取影响，其评定结果不是唯一的。

1.1.4 对角线法

对角线法是过实际被测要素的一条对角线的两端点连线、且平行于另一条对角线两端点连线的平面作为评定基准。同样，通过矩阵运算便可求得基准平面的法向量。同样，由于测量点的选取影响，其评定结果也不是唯一的。

1.2 面对面垂直度误差的评定

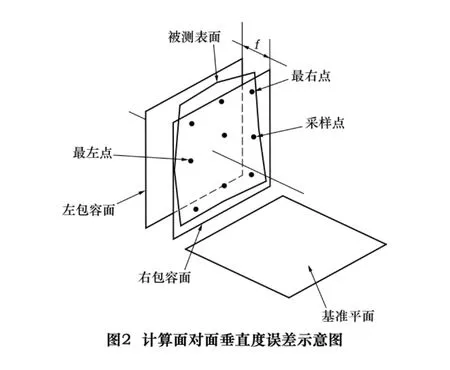
求得基准平面后，就可进一步求解被测实际表面对基准平面的垂直度误差。依定义，包容被测提取要素，并垂直于基准平面，且距离为最小的两平行平面间的距离，即为垂直度误差。如图2所示。

设在被测提取要素测得一系列采样点Mj（xj，yj，zj）（j=1，2，…，n）（n为测点数量），过各采样点做与基准平面垂直的平面族。设该平面族的法向量为（A2，B2，C2），它与前述求出的基准平面成垂直关系，因此，两平面的法向量成A1A2+B1B2+C1C2=0关系，即

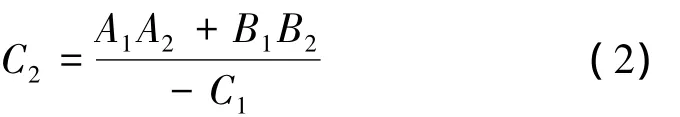
而根据平面点法式方程，设过被测采样点M1（x1，y1，z1）且垂直于基准平面的平面K的方程为

将式（2）代入式（3），得

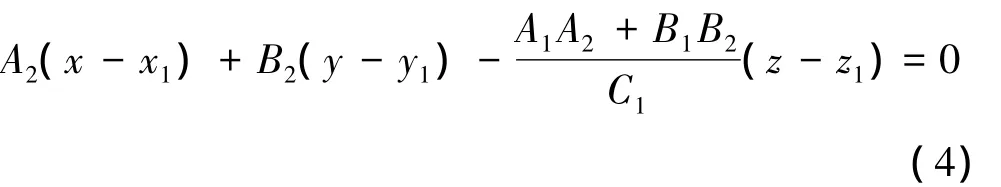
求所有被测采样点Mj（xj，yj，zj）到平面K的距离Ni为

目标函数F（A2，B2）={（Ni）max－（Ni）min}满足最小化时，F（A2，B2）的（A2，B2）以及通过公式（2）的计算即可得被测包容面的法向量F（A2，B2，C2），且该二元函数F（A2，B2）的最小值即为垂直度误差。因此垂直度误差评定就转化为求二元函数F（A2，B2）的最小值问题。

2 测量实例

笔者按前述的数学模型，利用MATLAB软件，编写了数据处理程序，并制作了友好界面，用户只需输入测点的数据，选择评定方法，就可得到基准要素的平面度误差值，以及被测要素的垂直度误差，并绘出误差图形［2－4］。

表1 测量数据

在万能工具显微镜上，用电感比较仪对图l所示零件进行测量，测得采样数据如表1所示。将测量数据输入系统界面，选择基准要素的评定方法，分别计算平面度及垂直度误差。计算结果见表2所示。

表2 测量结果

最小条件法计算界面如图3所示。界面左边为测量数据输入框，界面右侧为基准及被测表面的实际折面图。将实际折面图放大并旋转后得出，该图形下方为基准要素，上包容面过最高点10、12两点，下包容面过最低7、15两点，均平行于基准平面。从平面度误差最小区域判别准则上来看，该条件满足交叉准则，见图4所示。再从MATLAB的命令操作窗上再次证实:基准提取要素各采样点到基准平面的距离r=（－4.233 7－4.234 2－4.231 4－4.231 1－4.234 1－4.232 8－4.234 6－4.234 0－4.231 6－4.229 2－4.229 6－4.229 2 －4.234 1 －4.230 5 －4.234 6 －4.232 4）×103，也可看出10、12 点最高，距离－4.229 2×103μm，7、15点最低，距离－4.234 6×103μm，两者之差（4.234 6－4.229 2）×103μm=5.4 μm 即为平面度误差。

该图形左边为被测要素，右包容面过最近点13点，左包容面过最远8点。且都垂直基准平面。从命令窗上得到，被测提取要素各采样点到平面K的距离r=0 －2.399 9 －3.799 8 －7.699 7 －2.966 7 －6.566 6－6.966 5 －8.666 3 －3.333 3 －5.533 2 －4.933 1 －7.033 0 －0.000 1 －6.699 9 －7.399 8 －8.099 7，第 1点过平面K，距离为0。最近点13点与最远点8点的距离之差0.000 1－（－8.666 3）=8.666 4 μm，即为垂直度误差。经过以上对本系统4种处理方法的验证，结果都符合其建模原理。

3 结语

本文根据形状和位置公差的国家标准，建立面对面垂直度误差数学模型，利用数学软件MATLAB，来实现面对面垂直度的自动处理。检测人员只要从界面上输入实验测量数据，通过选择所需要的处理方法后便可直接得出平面度及垂直度误差值，并对测量表面进行三维显示，可清楚地反映出被测量的几何特征，及评定准则的应用情况，对计算结论进行验证。具有操作简单，数据处理速度快，不易出错，计算误差小，直观明了等优点。尤其是在处理测点较多，数据处理繁琐时，更能体现出它优越的运算功能。可有效提高高校实验室、企业员工检测中小型零件平面度、垂直度误差的工作效率。

［1］中华人民共和国国家标准GB/T 1958—2004:产品几何量技术规范（GPS）形状和位置公差检测规定［S］.北京:中国标准出版社，2005.

［2］张志涌.精通 MATLAB6.5版［M］.北京:航空航天大学出版社，2003.

［3］飞思科技产品开发中心.MATLAB 7基础与提高［M］.北京:电子工业出版社，2005.

［4］［美］Gerald Recktenwald.数值方法和 MATLAB 实现与应用［M］.伍卫国，方群，张辉，等译.北京:机械工业出版社，2002.