基于切削层形状的动态铣削力试验研究及建模*

牛兴华 杨中宝 卞扬清 马 超 尹文珊 崔 莹

（①天津理工大学天津市复杂系统控制理论及应用重点实验室，天津300384;②天津航天长征火箭制造有限公司，天津300462;③军事交通学院军事物流系，天津 300161）

铣削加工有多刃、断续切削和铣削力动态变化的特点。建立准确的动态铣削力预测模型，不仅是进行铣削工艺参数优化、铣刀选择、表面形貌预测和功率计算的前提，也是进行铣削物理仿真的基础。铣削时，切削层形状不断地变化，其与铣削力之间有密切的联系，切削层面积的变化可以反映出动态铣削力的变化规律。

1 单刃铣削临界条件及铣削力研究

1.1 单刃铣削临界条件

铣削加工中，对于不同切削用量组合，同时参与铣削的切削刃数目，交叠程度或断续间隔情况都会发生相应变化。本文研究单刃铣削条件下的动态铣削力。为精确建立动态铣削力预测模型，本文对顺铣方式下立铣刀侧铣加工单刃铣削的临界条件进行了分析。图1和图2中Zen为切削刃在切削角φen（如图1所示，φen=φmax－φmin为切削区域内最大圆弧所对应的圆心角）内的轴向投影距离，S为相邻切削刃的轴向距离。一般情况下Zen＜S，β为铣刀螺旋角，n为主轴转速。

为便于直观分析与计算，在此将切削层展开在平面上进行研究（如图2）。图1和图2所示为单刃铣削临界值（用轴向切深临界值表示）apcr＞Zen的情况，对于apcr＜Zen的情况可做同理分析。结合图1和图2a，由几何关系可得:

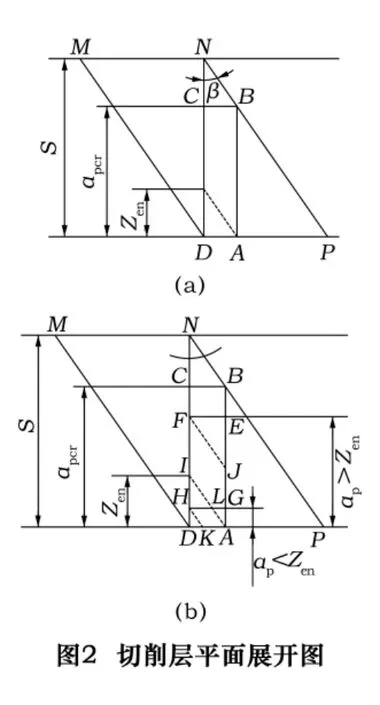
两相邻切削刃的轴向距离S可表示为:

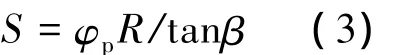
式中:齿间角φp=2π/z，z为铣刀齿数。

如图2a所示，当前一切削刃移动至PN位置且相邻的后一切削刃刚好移动至DM位置时，为两刃同时参与铣削的临界情况。点B和点D分别为前后切削刃的切出点和切入点。对于指定的铣刀，螺旋角β为已知，可得单刃铣削的临界条件为

在径向切深ae一定时，当轴向切深ap小于或等于其临界值apcr时，为单刃铣削，否则为多刃铣削。

1.2 铣削力研究

铣削力大小与铣削过程中的切削层面积有关［1］。如图1所示，考虑单刃铣削情况，在铣刀旋转过程中，随着切削层面积的变化铣削力随之发生改变。切削层面积受各切削用量的影响，其中切削厚度ac随每齿进给量f齿和径向切深ae的增加而增大（ae＜R时），进而导致铣削力增大。

（1）当ap≤apcr=S－Zen且ap＞Zen时，切削层AEFD如图2b所示。当切削刃经切入点D继续运动时，随着切削宽度（铣刀主切削刃参加工作的长度）的增加铣削力增大，到AI位置达到最大值。此后直至JF位置切削层面积保持不变，铣削力恒为定值。随后铣削力减小直至为零，到E点切出工件。

（2）当ap≤apcr=S－Zen且ap＜Zen时，切削层AGHD如图2b所示。由切入点D开始，随着切削宽度的增加铣削力增大，到KH位置达到最大值。此后切削宽度不变而切削厚度减小，铣削力缓慢降低直至AL位置。随后铣削力继续减小直至切出点G处变为零。

2 基于切削层形状的动态铣削力建模

2.1 铣削力模型分析

如图3所示，根据Altintas和Budak基于切削理论所建立的微元切削力模型［2－3］，可得铣刀切削刃任意一点处的微元切向切削力dFt和径向切削力dFr

式中:aci（φ，z）为瞬时未变形切削厚度;Ktc和Krc为前刀面铣削力系数;Kte和Kre为刃口系数。

相对于前刀面铣削力系数，铣削加工中刃口系数影响通常很小［4］。基于上述考虑，本文从切削层面积显著影响铣削力的角度出发，采用如下微元铣削力模型:

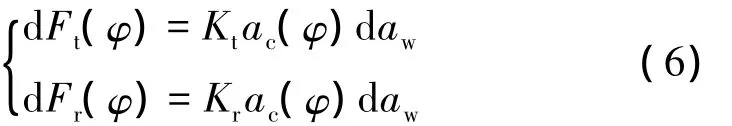
式中:ac（φ）为瞬时切削厚度;daw为微元切削宽度;Kt、Kr为铣削力系数;φ为铣刀位置角。

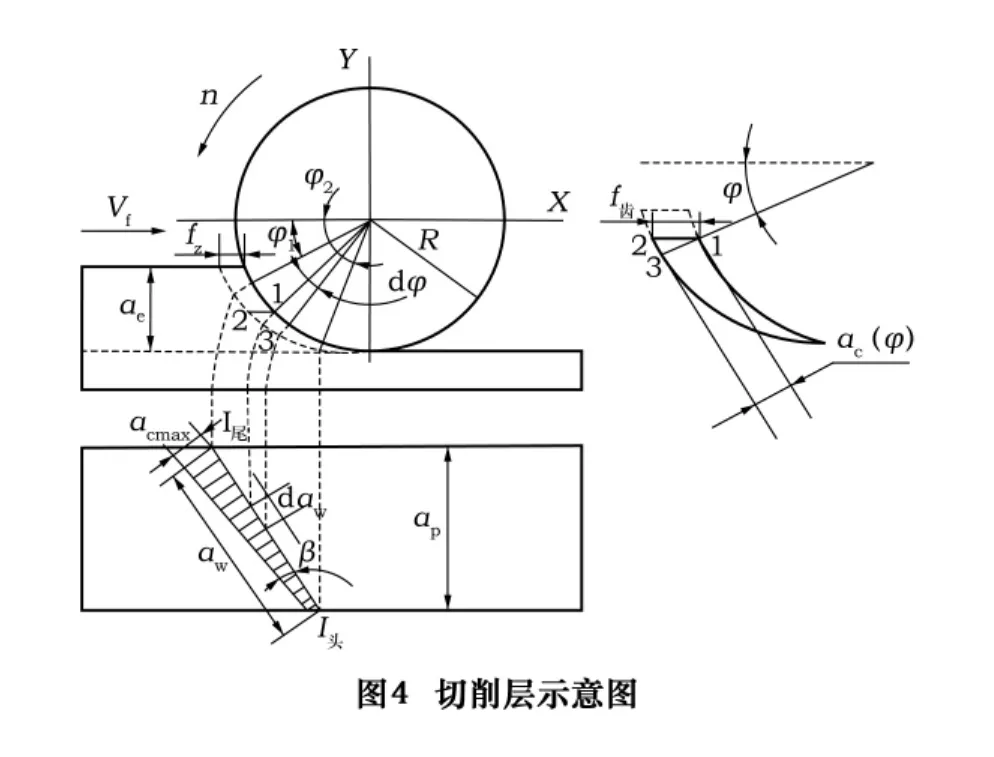
本文试验研究所采用的立铣刀螺旋角β=34.72°＞30°，故螺旋角的影响不可忽略［5］。由图4可得到离散化处理后的铣刀微元切削宽度

瞬时切削厚度可近似表示为:

本文采用压电式铣削测力仪测量进给抗力Fx（φ）和切深抗力Fy（φ）。通过图5受力分析可实现微元铣削力向X和Y方向的转换

考虑到铣削是断续切削的特点，为便于判断铣刀转至任意位置时切削刃是否参与铣削，故在此引入窗函数:

式中:φmin和φexit的定义参见图1，分别表示切削刃的最小切入角和最终切出角。联立式（6）～（10），经整理可得总的瞬时铣削力表达式

式中:φ1、φ2为切削刃转至任意位置时参与铣削切削刃的角度积分限。为了避免轴向积分的繁琐计算，本文采用了角度积分方法求解铣削力模型。

2.2 铣削力系数确定

根据文献［6］可知，有偏心铣刀与相同参数的无偏心铣刀在回转一周过程中的材料切除量相同，且平均铣削力与螺旋角无关，可得

式中:q=t、r，i=x、y，φp为齿间角;φst和 φex分别为铣刀切入角和切出角。

对于无螺旋角的直齿铣刀，瞬时铣削力力学模型的表达式如下

通过铣削力的坐标转换并进行积分整理可得

进而可得铣削力系数的表达形式如下

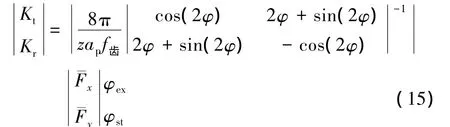
结合本文研究情况，在无偏心直齿铣刀铣削时，铣刀切入角φst和切出角φex分别为

3 动态铣削力正交实验

3.1 试验条件

铣削试验是在YCM－V65A型四轴联动立式加工中心上进行，动态铣削力测量采用YDX－Ⅲ9702型压电式铣削测力仪。图6为铣削力测量试验原理图，铣削力测量试验现场如图7所示。试件材料为冷作模具钢Cr12（HB233）;铣刀为含铝高速钢立铣刀，铣刀齿数4，直径10 mm，螺旋角为34.72°。试验保证单刃侧铣;干切削，顺铣。

3.2 正交实验方案

动态铣削力正交实验研究考虑轴向切深ap、每齿进给量f齿、径向切深ae和主轴转速n因素的影响。每个因素取4个水平值，即采用L16（44）标准正交表安排试验，正交实验取值见表1。图8为试验测得的一组动态铣削力曲线。

表1 正交实验取值表

4 试验数据分析与模型验证

4.1 铣削力系数预测模型

利用铣削测力仪测得了进给方向和径向切深方向的动态铣削力，通过对动态铣削力测量数据进行处理得到两个方向的平均铣削力。采用前述原理，利用平均铣削力可计算出铣削力系数。对于一定的切削用量组合，可以假设铣削力系数和切削参数符合多项式模型。通过回归方程的最优选择所确定的铣削力系数辨识模型如下:

对16组正交实验数据进行回归分析，所得回归系数见表2。应用上述系数预测模型对16组正交实验进行系数验证，切向和径向铣削力系数平均计算误差分别为2.33%和5.18%，最大误差分别为7.13%和9.13%，均在允许误差（10%）范围内，说明系数模型具有较强的辨识能力。

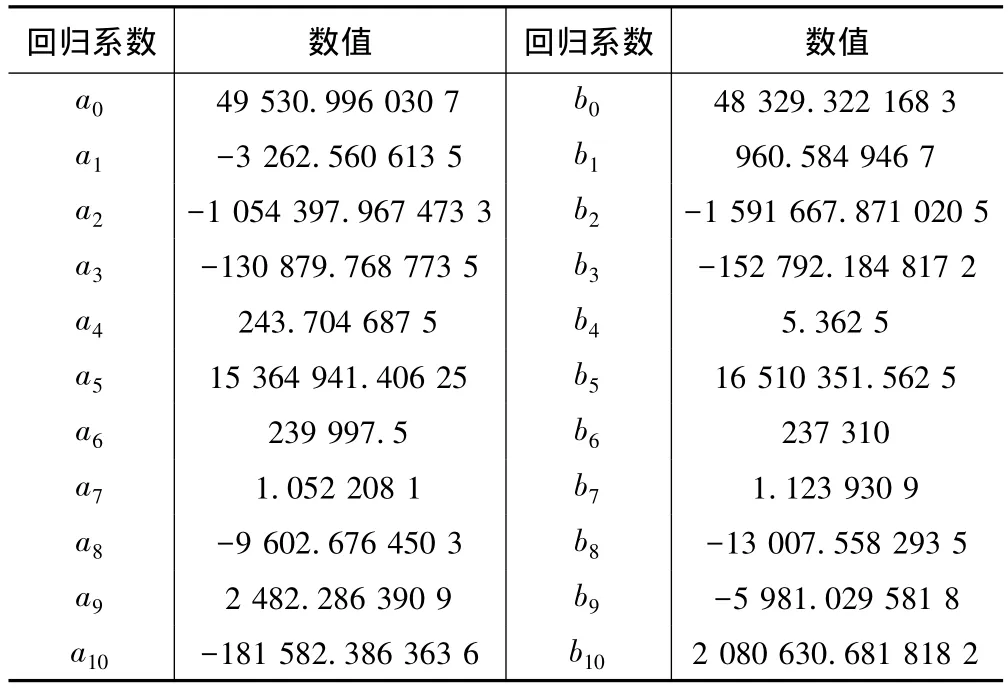
表2 模型回归系数计算值

表3 模型预测与实际测量数值对比

4.2 动态铣削力模型验证与仿真

为检验动态铣削力预测模型的适用性和预测精度，应用上述模型对另外8组试验数据进行模型预测值和实际测量值的对比，图9为两组动态铣削力仿真和实测对比曲线，数据对比结果如表3所示。预测模型的最大误差为10.62%，进给方向和径向切深方向的平均计算误差分别为4.51%和6.56%，说明模型具有较高的预测精度。

图9表明，动态铣削力仿真和实测曲线无论在形状、幅值、变化趋势以及非切削时段间隔等方面都十分吻合，说明所建动态铣削力模型具有较强的适用性及预测能力。试验中，铣刀不同切削刃半径的偏差、连续试验下的刀具磨损以及工艺系统的变形等方面原因，造成实测曲线和预测曲线在稳定铣削时段铣削力曲线平台存在差异，甚至于产生波动。

5 结语

本文对立铣刀侧铣过程中动态铣削力进行试验研究及模拟仿真，在分析单刃铣削条件的基础上进行试验方案设计，最终建立了立铣刀侧铣加工（顺铣）冷作模具钢Cr12的动态铣削力模型。模拟仿真和实测结果的吻合，说明了所建模型的适用性及准确性。本研究为铣削工艺参数优化和物理仿真奠定了基础。

［1］Tlusty J，Mac Neil P.Dynamics of cutting forces in end milling［J］.CIRP Annals，1975，24:21－25.

［2］Altintas Y，Lee P.Mechanics and dynamics of ball end milling［J］.Transactions ASME，Journal of Engineering for Industry，1998，120（4）:684－692.

［3］Budak E，Altintas Y，Armarego E J.Prediction of milling force coefficients from orthogonal cutting data［J］.Transactions ASME，Journal of Manufacturing Science and Engineering，1996，118（2）:216－224.

［4］尹力，刘强.基于偏最小二乘回归（PLSR）方法的铣削力模型系数辨识研究［J］.机械科学与技术，2005，24（3）:269－272.

［5］杨蕾，史耀耀，杨巧凤，等.钛合金TC11铣削力分析与建模［J］.制造技术与机床，2007（1）:35－37.

［6］Kline W A，Devor R E.The prediction of cutting forces in end milling with application to cornering cuss［J］.MTDR，1982，22（1）:7－22.