产出、通货膨胀预测与利率期限结构——基于无套利动态NS模型

贺畅达

(东北财经大学研究生院，辽宁 大连 116025)

一、问题的提出及文献综述

利用利率期限结构本身信息预测宏观经济变量的相关研究可分为两类:第一类主要利用不同到期期限的期限价差作为利率曲线的斜率对产出及通货膨胀进行预测。Harvey的开创性研究发现期限利差 (或利率曲线的斜率)对实际消费增速有稳定的预测能力［1］。Stock和Watson提出一致与领先指标模型，用期限利差作为一种重要的领先指标［2］。Estrella和 Hardouvelis进一步研究了利率曲线斜率对实际经济的预测能力［3］。Mishkin发现不同到期期限的利率之差可以预测未来相应期限通货膨胀的变化［4］。Estrella和Mishkin分析了美国以外的欧盟国家也存在这种利率曲线的曲率对经济和通货膨胀的预测能力［5］。Estrella和Trubin认为利率曲线斜率利用实时数据预测衰退时表现良好［6］。Kauppi和Saikkonen用动态Probit模型考察利率价差对经济衰退的预测能力，发现动态Probit模型的预测效果明显强于传统的静态Probit模型，并且利率价差一直是重要的预测变量［7］。Rudebusch和Williams认为利率曲线斜率对美国经济衰退的预测能力强于专业预测者调查［8］。第二类利用宏观金融模型研究利率曲线的潜在成分 (因子)与宏观经济变量的关系。宏观金融模型包括将利率分解为三个潜在主成分的无套利宏观金融模型以及基于Nelson－Siegel模型［9］将利率期限结构分解为水平 (Level)，斜率 (Slope)和曲率(Curvature)三个潜在因子的宏观金融模型。Ang和Piazzesi最早将宏观经济变量引入利率期限结构仿射模型，提出无套利宏观金融模型［10］。Ang等认为利用无套利宏观金融模型中利率曲线的前两位的主成分，可以提高模型对经济增长的预测能力［11］。Wright用 Probit模型预测美国经济衰退时，发现利率期限的形状包含衰退可能性的信息要多于期限利差［12］，这说明利用利率曲线潜在因子所包含的信息要大于第一类研究中常用的期限利差所含的信息。另一种宏观金融模型拓展了Nelson－Siegel模型 (NS宏观金融模型)，Diebold和Li首先利用DL两步法从利率曲线中提取出时变的 (动态)水平、斜率和曲率三因子［13］;随后，Diebold 等［14］在 DL模型中加入产出、通货膨胀和联邦基金利率，考察利率曲线三因子与宏观经济变量的交互作用，结果表明宏观变量与利率曲线具有相互的双向影响。在宏观金融模型框架下，学者发现利率曲线的水平因子与通货膨胀之间具有显著的相关性，Rudebusch和Wu就认为水平因子反映了通货膨胀预期［15］。Moench认为利率曲线斜率的意外变化对产出造成的影响很小，而曲率对宏观经济有预测作用，曲率的正冲击会导致利率曲线变得扁平，并且显著降低一年后的产出［16］。Ang等利用宏观金融模型将利率曲线分解为时变的三因子来描述利率曲线的形状，进而对宏观经济与利率曲线的三因子利用时变VAR模型进行相应实证分析［17］。

在国内，郭涛和宋德勇认为由于流动性过剩和传导机制不完善等原因，我国的长短期利差仅反应了同期通货膨胀，而没有对未来通货膨胀的预测能力;利用Nelson－Siegel模型分离出来的水平因子与未来的通货膨胀具有协整关系［18］。石柱鲜等用无套利宏观金融模型方法，研究表明利差对经济增长具有一定的预测能力，对通货膨胀的预测能力较弱;经济增长与通货膨胀的正冲击对利差分别会造成负向和正向的影响［19］。吴吉林利用NS宏观金融模型分析利率期限结构潜在变量与宏观经济变量之间的关系，发现水平因子包含预期通货膨胀信息;斜率因子反应货币政策变化，包含经济增长信息;曲率因子的经济学含义不明显［20］。李宏瑾等利用Mishkin的方法考察利率期限结构对通货膨胀的预测能力，发现我国利率曲线的中短端对通货膨胀的预测能力较强［21］。康书隆和王志强利用DL方法估计中国的利率期限结构，研究利率期限结构的风险特征及内含信息，发现长期利率超前于CPI序列变动，长短期利差与经济景气指数一致变动［22］。姚余栋和谭海鸣利用无套利仿射利率期限结构模型中分离出水平向量Level，通过与居民通货膨胀预期和经济学家通货膨胀预期的比较认为水平向量可以代表金融市场的中长期通货膨胀预期［23］。此外，刘春航和王清容利用利率曲线反转对经济衰退的预测作用和房地产周期以Probit模型研究美国经济周期的可预测性，研究表明利用利率曲线与房地产周期信息联合预测的能力较强［24］。但是，由于三十余年的改革开放使我国经济始终保持高速增长，极少出现经济衰退的情况，而且数据也表明我国的国债利率期限结构也极少出现反转的情况，在利用国外研究中常用的二元选择模型判断我国的利率曲线变化与经济预测能力的稳定性时存在如何界定因变量取值的问题，因此相关文献较少。

对于以上研究我们发现三个问题:第一，无论国内还是国外的研究中常用到利率曲线长短期利差预测经济增长与通货膨胀，这种方法虽然简便，但其只是斜率的一个代理变量，并不能包含曲线的斜率的所有信息，因此需要找到能够全面刻画利率曲线变化特点的变量。第二，无套利宏观金融模型虽能将利率曲线分解为三因子，却不能很好地解释三因子，而且无套利模型存在样本外预测能力较弱的限制。第三，NS宏观金融模型虽能分解利率曲线为水平、斜率以及曲率的三因子，但却又缺乏无套利理论的支持。因此，有必要找到既有理论基础又可以较好地拟合和预测利率期限结构动态变化特点，还具有明确经济意义的因子的利率期限结构模型。Christensen等［25］建立的引入无套利约束 Nelson－Siegel模型，即无套利动态NS模型 (AFDNS)就解决了以上几个问题。无套利NS模型集合动态NS模型的较强预测能力、潜在因子有明确的经济含义和无套利模型的理论基础。我们的经验结果表明，无套利动态NS模型在利用我国国债数据来动态估计利率期限结构时效果良好。

本文首次尝试采用无套利NS模型(AFDNS)估计出的利率曲线的水平、斜率及曲率三因子，利用三因子对宏观经济变量进行预测，考察我国的利率期限结构所蕴含的宏观经济信息，并且与常用期限利差对宏观变量的预测能力进行比较。

二、数据的选取及处理

国债数据。本文利用国债价格及期限等信息估计利率期限结构，这就要求选择定价合理的债券作为数据样本。目前，我国债券二级市场主要由银行间债券市场和交易所债券市场两部分组成。虽然2010年10月证监会、银监会和人民银行等部门宣布上市银行可以参与交易所债券市场，这也标志我国债券市场分割的状况开始改变。但是，目前两个市场仍然存在托管、清算、结算系统分离以及市场主要参与者不同等问题。在某些交易时间，同种债券在同一时间、不同的市场价格仍然明显不同。通过比较，决定选用2002年1月到2012年4月的银行间市场的国债交易月度数据，并剔除异常价格的债券作为本文的样本数据，再用Fama－Bliss方法［26］从国债价格中剥离得到离散的即期利率作为模型估计的先验数据。

通货膨胀。反应我国价格水平的指标有消费者价格指数 (CPI)，商品零售价格指数 (RPI)以及GDP平减指数等。尽管近年来有关CPI对物价水平真实反应程度存在争议，但是考虑到RPI等数据代表性的局限以及GDP平减指数的可得性和频度等问题，本文最终选择以CPI数据来表示国内的通货膨胀率。用国家统计局公布并由Wind资讯提供的的样本区间从2002年1月到2012年4月的以2000年12月为100的定基CPI指数来表示国内的通货膨胀水平，并进行季节性调整。最后利用式 (1)来表示年化的通货膨胀变化率:

其中，h表示预测的期限 (月)，CPIt表示在第t期时CPI的水平，πt+h表示从当前的第t月到未来的第t+h月通货膨胀变动的比率。

产出。本文采用国家统计局公布并修订后的累计GDP数据，计算差值得到名义GDP的季度值。通过线性插值法将季度数据分解为月度数据［19］。为了单独考察经济增长排除通货膨胀因素，利用公式实际GDP=100(名义GDP/CPI)将名义GDP转化为以2000年12月物价为基础的实际GDP。再利用X－11方法剔除实际GDP的季节性影响。①考虑到中美之间的节假日不同，用X－12方法对我国数据进行季节性调整并不适合，因此本文用X－11方法对实际GDP等变量进行季节性调整。最后利用式 (2)表示年化实际GDP的变化率:

其中，GDPt表示在第t期时实际GDP的水平，yt+h表示从当前的第t月到未来的第t+h月实际GDP变动的比率。

三、利率期限结构动态因子:基于AFDNS模型的估计

1.AFDNS模型

Christensen等［25］的研究证明在无套利约束下，仿射利率期限结构模型具有NS因子形式。经验表明:三因子的无套利动态NS模型(AFDNS)形式简洁，样本内动态估计和样本外预测能力较强，而且能够较好地刻画我国利率期限结构动态变化特征，因此本文采用AFDNS模型估计利率期限结构，并提取利率期限结构的水平、斜率及曲率三个动态因子。AFDNS模型可以表示为 (3)—(4)式的形式:

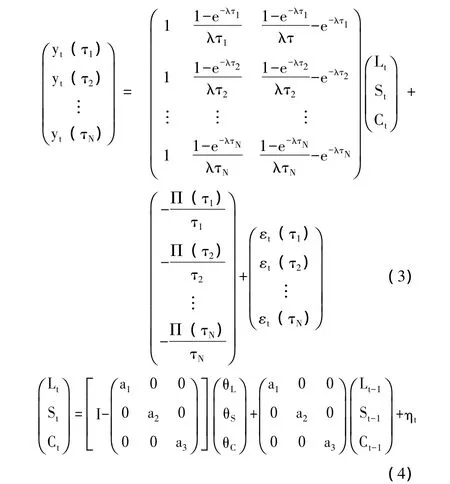
其中，yt(τi)表示t时刻到期期限为τi的零息债券利率，λ表示指函数的衰减率参数，也决定曲率因子曲线最值位置，－Π (τi)/τi表示AFDNS模型的无套利调整项，状态变量Lt、St和Ct分别表示利率期限结构的水平、斜率和曲率因子，在风险中性Q－测度下三因子动态变化过程服从 (4)式的形式。

2.AFDNS模型的估计与状态变量的提取

将利率期限结构AFDNS模型用状态空间形式表示，利用卡尔曼滤波法估计该模型的参数(具体结果如表1所示)，结果显示AFDNS模型对各期限的利率期限结构拟合程度较高。

表1 AFDNS模型参数估计结果

我们再利用卡尔曼平滑方法提取AFDNS模型的利率期限结构状态变量，在图1中分别表示为水平因子、斜率因子和曲率因子三个时间序列。其中，水平因子序列全部位于零点线以上，斜率因子大部分都小于零，曲率因子则不规则地围绕零线上下波动。图2显示在λ为1.25时，AFDNS模型三因子的载荷因子 (Loading Factor)。

将从AFDNS模型中提取出的水平因子与到期期限为10年的长期利率曲线列于图3中，二者的走势相似，数据显示水平因子与长期利率的相关系数为0.94，二者高度正相关。说明利率期限结构的水平因子包含长期利率的信息，同时也包含未来通货膨胀的信息。将斜率因子与1年期和10年期利差序列共同在图4中表示，两序列的相关系数为0.79，二者也有较高的相关性。这说明利用AFDNS模型提取出的动态因子可以较好地反映利率期限结构的形态及动态，可以用动态因子来考察利率期限结构与宏观经济动态关系。

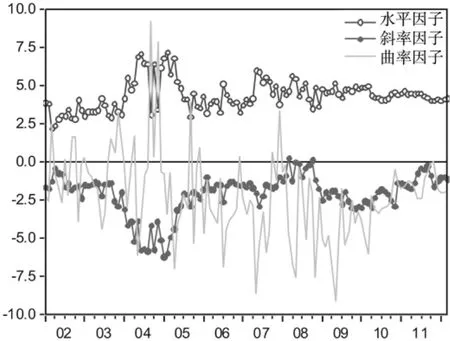
图1 AFGNS模型估计的三因子

图2 AFDNS模型载荷因子

图3 水平因子与10年长期利率

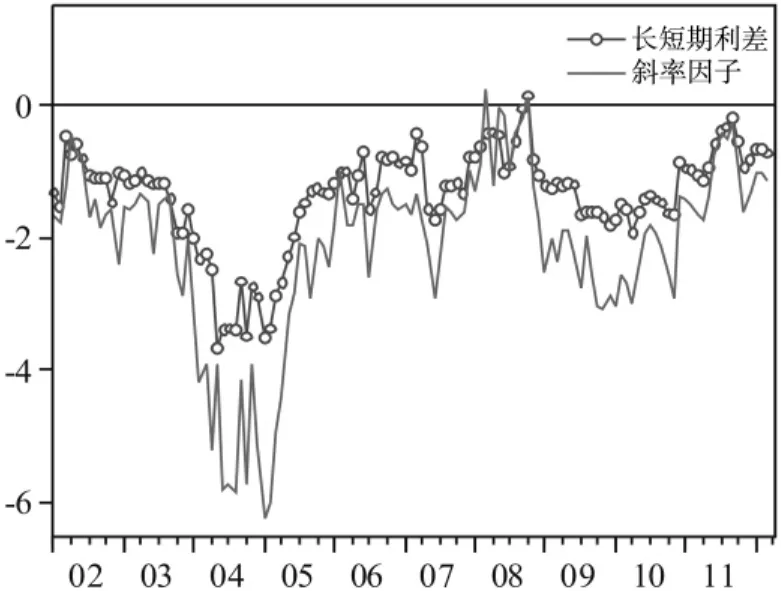
图4 斜率因子与长短期利差

四、利率期限结构动态因子与宏观经济变量的预测

1.利率期限结构对产出的预测

经验研究显示，期限利差 (Spread)对经济增速具有预测作用，是判断经济增长的先行指标。本文利用AFDNS模型提取利率期限结构的潜在因子，这些潜在因子是否也具有对经济增长的预测效率，而且相比较期限利差谁的预测能力更强，这就需要通过比较考察。

为考察利率期限结构对实际产出的预测能力，我们首先对相关数据进行单位根及协整检验，结果表明:AFDNS模型的水平因子和斜率因子序列都存在单位根，斜率因子是平稳序列，期限利差和各期限未来实际GDP增长率也都服从单位根过程。Johansen检验的结果显示各期限GDP增长率分别与三因子及期限利差均存在协整关系。最后，利用式 (5)作为判断利率期限结构预测能力的计量模型:

其中，β0是方程的常数项，Xit是所考察的预测变量，εt是白噪声。

表2中所列是以AFDNS模型的动态因子(Lt，St，Ct)作为对未来产出的预测变量，我们考察三因子对 1，2，3，4，5，6，7，8，9，10，12，18，24个月GDP增速的解释能力。结果显示，水平因子Lt、斜率因子St与曲率因子Ct除对k=1的产出增长的解释在10%的置信度下仍不显著，对其余不同期限产出增速均具有显著的解释力，说明三因子对GDP增速有显著的预测能力。而且，水平因子Lt、斜率因子St和曲率因子Ct的系数均为负，三因子的增加都意味着未来的经济增速将下滑，反之则上升。对结果的经济解释是:水平因子Lt代表长期利率，当长期利率增加时，说明未来的政策将进入紧缩期，未来的经济增速也会下降;由于斜率因子St大多为负 (即大部分时间长期利率大于短期利率)，当斜率因子增加时 (即斜率的绝对值减小)，长短期利差变小也会是未来经济增速下降的信号;曲率因子Ct的增加会明显提高利率期限结构的中短端，使利率曲线更趋近于驼峰形状，这也是未来经济将下滑的紧缩信号。从模型的解释力角度，三因子对未来经济变化的解释力中，对12个月的预测能力最强，可以解释超过40%的未来经济变化。

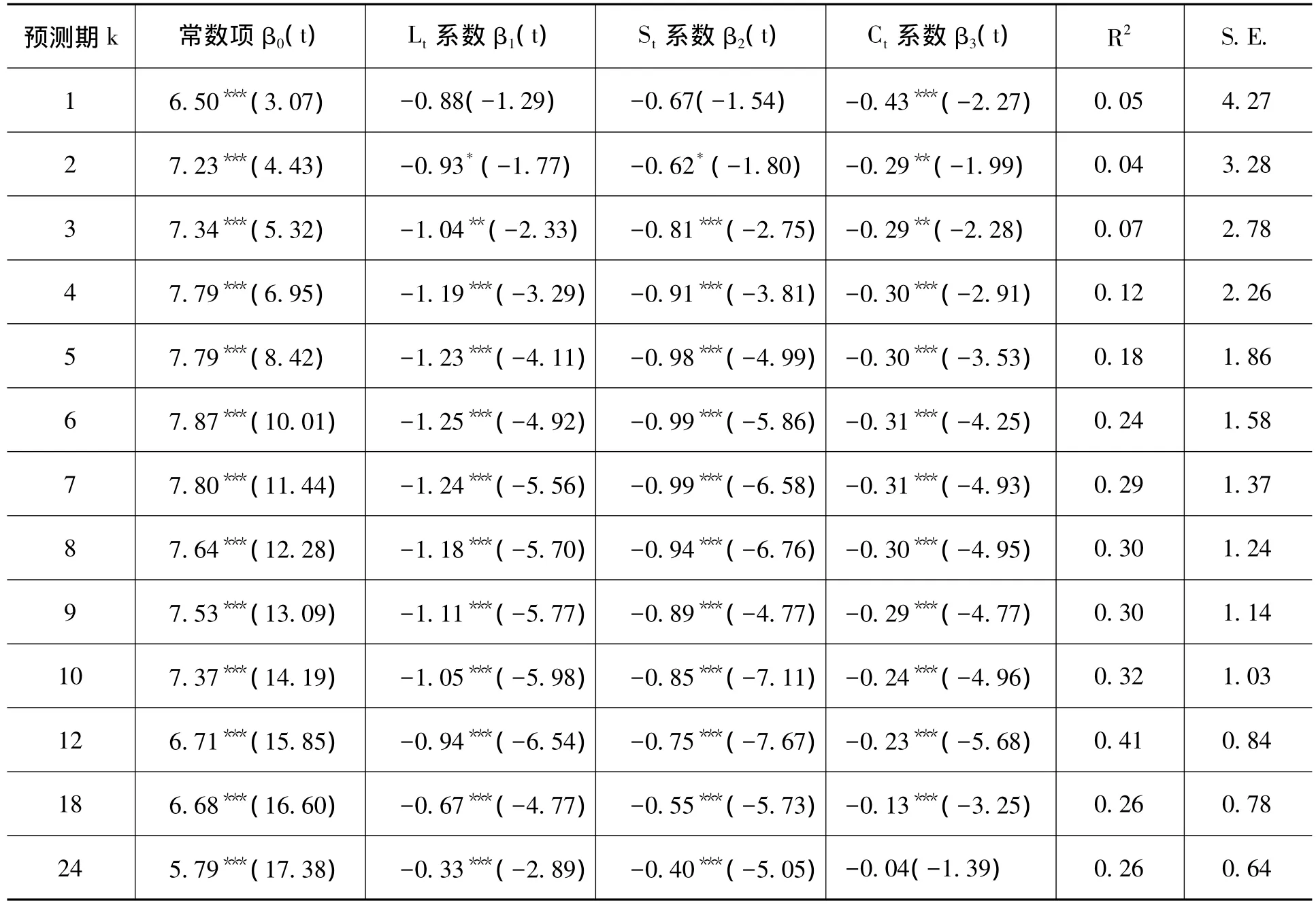
表2 利用AFDNS模型动态因子对产出的预测

表3中所列是以1年与10年的期限利差Spread及10年的长期利率Y10作为对未来实际GDP增速进行预测。结果显示，期限利差Spread和长期利率Y10，除对未来1月和2月的产出增长的解释能力不明显，对其他各期限GDP增速的预测能力都显著。与其他学者对国外利差的经济预测能力的检验相同，Spread增加(利差绝对值减小)预示未来的经济增长将放缓;长期利率与未来经济增速的变化方向相反。期限利差和长期利率与三因子模型一样对未来12个月的经济增长的预测能力最强，可以解释34%的经济增长的变化。

表3 利用期限利差Spread及长期利率Y10对产出的预测

比较表2和表3中利用AFDNS模型三因子和传统的利差对我国经济增长的预测，我们发现，三因子都含有对经济增长率显著的预测能力，含有未来经济变动的信息;期限利差Spread也具有对我国经济的预测能力;而且利用三因子的解释 (预测)能力更强 (除对未来24个月的预测)。这首先是因为AFDNS斜率Slope等因子是从利率曲线分解出的真正斜率，期限利差Spread是斜率的一种代理变量，而且期限利差也存在如何选取的问题。利用三因子模型所包含的关于利率曲线的信息要多于期限利差和长期利率模型。所以利用AFDNS模型三因子对经济的预测能力相比于利用期限利差等利率期限结构代理变量的预测能力更强。此外，我们还注意到无论用利差还是三因子对GDP的预测，对未来经济12个月的预测能力都最强。

2.利率期限结构对通货膨胀的预测

我国的利率期限结构对通货膨胀及通货膨胀预期的可预测相关研究中，部分学者认为利差对通货膨胀的预测作用不明显［18－19］;也有学者认为利差包含未来通货膨胀的预期［26］。而利用无套利模型或Nelson－Siegel模型的研究中均发现利率期限结构的水平因子对通货膨胀具有预测能力［18－23］。这就使我们需要回答以下问题:利率期限的斜率 (期限利差Spread或AFDNS模型的斜率因子Slope)是否包含通货膨胀未来变动的信息?结合Nelson-Siegel模型与无套利模型的AFDNS模型的水平因子和曲率因子是否具有对通货膨胀或通货膨胀预期的信息?

为考察利率期限结构对通货膨胀率的预测能力，首先，对未来各期限通货膨胀变化率进行单位根检验，结果显示各期限通货膨胀率均服从一阶单整I(1)过程。其次，Johansen检验的结果显示各期限通货膨胀变化率分别与三因子及期限利差均存在协整关系，可以进行协整建模。最后，利用式 (6)作为判断利率期限结构预测能力的计量模型:

其中，β0是方程的常数项，Xit是所考察的预测变量，εt是白噪声。

利用AFDNS模型的三因子对通货膨胀预测的实证结果显示，三因子对1年内的通货膨胀变化预测能力很弱，而且各因子对模型的解释力也不显著，但是，对于超过1年期的通货膨胀则具有显著的预测能力。我们选取12个具有代表性的方程 (回归结果列于表4)，从各方程的拟合优度R2判断，AFDNS的三因子预测模型对23和24个月后的通货膨胀解释能力最强，即利用利率期限的三因子预测未来两年的通货膨胀效果最好。

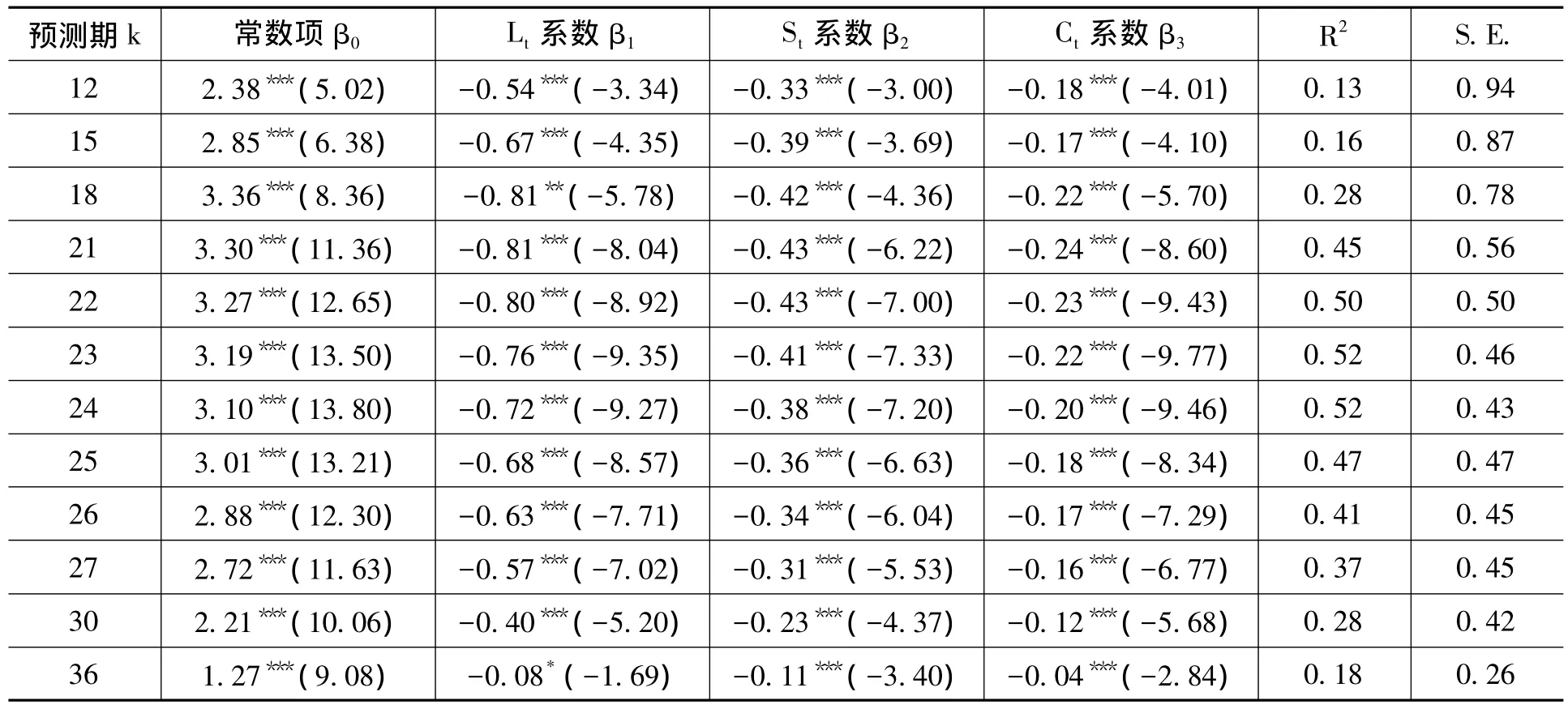
表4 利用AFDNS模型动态因子对通货膨胀的预测

三因子预测模型中，水平因子Lt、斜率因子St和曲率因子Ct的回归系数均为负，表明当三因子的值增加时，都会降低未来的通货膨胀。从经济意义上，水平因子Lt的提高，通常意味着经济已经开始繁荣，经济增速加快，通货膨胀高启，经济有过热的趋势，这时央行会利用货币政策提高短期利率，进而影响长期利率，以使经济降温，通常情况下短期利率提高的幅度会大于长期利率，使得利率曲线的斜率变小 (由于斜率因子为负值，斜率变小意味着斜率值增大)，St增加，经济将进入紧缩周期，未来的通货膨胀及通货膨胀预期将下降。此外，曲率因子Ct的提高也会使利率曲线的短期端上升，中期利率上升更快，利率曲线的驼峰形状更明显，长短期的利差也将缩小，同理，也会造成未来通货膨胀的下降。因此，AFDNS三因子的增加都预示着未来的通货膨胀率下降。而通货膨胀对利率期限结构变动的反应较经济增速要慢，实证结果显示，利率曲线的变化能够对1年以后的通货膨胀有预测能力，而且对两年左右的预测能力最强，可以解释50%以上的未来通货膨胀变化。

我们还注意到，单独利用AFDNS模型的任一个或两个因子对通货膨胀的预测能力都会比使用三因子共同进行预测的能力明显下降。同样我们还利用期限利差Spread对通货膨胀进行预测，结果显示仅利用期限利差的预测效果不明显;单独使用长期利率对通货膨胀具有较弱的预测能力;结合长期利率与期限利差共同对通货膨胀进行预测，大大提高预测能力，但预测能力仍明显弱于利用AFDNS模型三因子的预测能力。

综上，我们利用AFDNS模型的动态三因子分别对产出 (实际GDP)和通货膨胀未来的变化率进行预测，结果显示联合利用三因子对产出增长率有显著的预测能力，对未来12个月的预测能力最强;对通货膨胀的预测结果显示，三因子不能解释未来1年内的通货膨胀变化，但是对未来1—3年的预测能力显著，而且对于两年左右的通货膨胀变化的预测能力最强，我们还在上文对检验结果进行了经济学解释。为了与传统文献常用的期限利差进行比较，我们还利用期限利差及长期利率对产出及通货膨胀进行预测，发现利用期限利差和长期利率的预测能力在对产出和通货膨胀进行预测时都弱于利用AFDNS模型三因子的预测能力。

［1］ Harvey， C.R.The Real Term Structure and Consumption Growth［J］. Journal of Financial Economics，1988，22(2):305－333.

［2］ Stock，J.，Watson，M.New Indexes of Coincident and Leading Economic Indicators［R］.NBER Working Paper No.R1380，1990.

［3］ Estrella，A.，Hardouvelis，G.A.The Term Structure as a Predictor of Real Economic Activity［J］.Journal of Finance，1991，21(9):555－576.

［4］ Mishkin，F.S.What does the Term Structure Tell Us about Future Inflation?［R］.NBER Working Paper No.2626，1990.

［5］ Estrella，A.，Mishkin，F.S.The Predictive Power of the Term Structure of Interest Rates in Europe and the United States［J］.European Economic Review，1997，41(7):1375－1401.

［6］ Estrella，A.，Trubin，M.The Yield Curve as a Leading Indicator:Some Practical Issues，Federal Reserve Bank of New York［R］.Unpublished Working Paper，2006.

［7］ Kauppi，H.，Saikkonen，P.Predicting US Recessions with Dynamic Binary Response Models［J］.The Review of Economics and Statistics，2008，90(4):777－791.

［8］ Rudebusch， G.D.， Williams， J.C.Forecasting Recessions:The Puzzle of the Enduring Power of the Yield Curve［J］.Journal of Business and Economic Statistics，2009，27(4):492－503.

［9］ Nelson，C.R.，Siegel，A.F.Parsimonious Modeling of Yield Curves［J］.The Journal of Business 1987，60(4):473－489.

［10］ Ang，A.，Piazzesi，M.A No － Arbitrage Vector Autoregression ofTerm StructureDynamicswith Macroeconomic and Latent Variables［J］.Journal of Monetary Economics 2003，50(4):745－787.

［11］ Ang，A.，Piazzesi，M.，Wei，M.What does the Yield Curve Tell Us about GDP Growth?［J］.Journal of Econometrics 2006，131(1－2):359－403.

［12］ Wright，J.The Yield Curve and Predicting Recessions［R］.FEDS Working Paper，2006.

［13］ Diebold，F.X.，Li，C.Forecasting the Term Structure of Government Bond Yields［J］.Journal of Econometrics，2006，130(2):337－364.

［14］ Diebold，F.X.，Rudebusch，G.D.，Aruoba，S.B.The Macroeconomy and the Yield Curve:A Dynamic Latent Factor Approach［J］.Journal of Econometrics，2006，131(1－2):309－338.

［15］ Rudebusch，G.D.，Wu，T.A Macro－Finance Model of the Term Structure，Monetary Policy and the Economy［J］.The Economic Journal，2008，118(7):118，906－926.

［16］ Moench，E.Term Structure Surprises:The Predictive Content of Curvature，Level，and Slope［J］.Journal of Applied Econometrics，2012，27(4):574－602.

［17］ Ang，A.，Boivin，J.Dong，S.，Loo－Kung，R.Monetary Policy Shifts and the Term Structure［J］.The Review of Economic Studies，2011，78(2):429－457.

［18］ 郭涛，宋德勇.中国利率期限结构的货币政策含义［J］. 经济研究，2008，(3):39－47.

［19］ 石柱鲜，孙皓，邓创.中国主要宏观经济变量与利率期限结构的关系:基于VAR_ATSM模型的分析［J］. 世界经济，2008，(3):53－59.

［20］ 吴吉林，金一清，张二华.潜在变量、宏观变量与动态利率期限结构——基于DRA模型的实证分析［J］. 经济评论，2010，(1):80－88.

［21］ 李宏瑾，钟正生，李晓嘉.利率期限结构、通货膨胀预测与实际利率［J］.世界经济 ，2010，(10):120－138.

［22］ 康书隆，王志强.中国国债利率期限结构的风险特征及其内含信息研究［J］.世界经济，2010，(7):121－143.

［23］ 姚余栋，谭海鸣.中国金融市场通货膨胀预期——基于利率期限结构的量度［J］.金融研究，2011，(6):61－70.

［24］ 刘春航，王清容.美国房地产周期与经济衰退的可预测性研究［J］. 金融研究，2008，(2):1－12.

［25］ Christensen，J.H.E.，Diebold，F.X.，Rudebusch，G.D.The Affine Arbitrage－Free Class of Nelson－Siegel Term Structure Models［J］.Journal of Econometrics，2011，9(1):4－20.

［26］ Fama，E.F.，Bliss，R.R.The Information in Long－Maturity forward Rates［J］.The American Economic Review，1987，77(4):680－692.