抵押资产组合对信用利差期限结构的影响分析

王雪标，周生宝，胡继真

(东北财经大学 数学与数量经济学院，辽宁 大连 116025)

一、引 言

目前，全球金融体系正经受着较大的信用风险和信用损失，而逐步开放的中国金融行业正面临金融风险与信用风险的重大考验。研究构建信用风险模型，正确估计与评价信用风险，对中国来说显得尤为重要。信用风险由两部分组成:一是违约风险，指交易一方不愿或无力支付约定款项致使交易另一方遭受损失的可能性;二是信用价差风险，指信用价差的变化而导致的损失。因此，信用风险模型主要研究信用风险违约问题和信用利差期限结构。信用风险的模型主要分为结构式模型和简化式模型。结构式模型在完全信息假设下，对公司资产价值演化过程建模。Merton［1］在Black－Scholes期权定价方法的基础上，在完全信息假设下，建立了以公司资产价值演化为基础的信用风险模型;公司是否发生违约由公司的资产价值来决定，当资产值低于某个门限值时视为违约，违约支付仅仅在合约终止时刻。Jarrow和Turnbull［2］以及Duffie和Singleton［3］给出了简化式模型。简化式模型是在不完全信息 (市场信息)假设下，对债务人违约强度和状态变量之间的函数关系建模，这使得简化式模型更现实一些，但是违约过程缺乏清晰的经济学解释。Jarrow和Protter［4］研究表明，结构式模型与简化式模型的内在联系在于所考虑的信息集不同。简化式模型有很强的样本内拟合性质、很弱的样本外预测能力。结构式模型的完全信息假设其实是一种近似假设，它是描述不同公司的运营差别的最简单办法。

Leland和Toft［5］以及Chen和Kou［6］研究表明，信用价差具有以下典型特征:信用价差可以不收敛到零;信用价差可以是上升型、下降型和驼峰型;信用价差与无风险率负相关。Merton在利率是常数的情形下，研究了信用利差期限结构，结果表明信用利差期限结构是驼峰型的。后来，Longstaff和Schwartz［7］将其进行了扩展，利率为随机利率情形，同时还考虑了破产成本、绝对优先规则因素，结果表明信用价差期限结构似乎没有改进。Sarig和Warga［8］以42家公司发行的137只零息债券作为样本，从实证角度考察了驼峰型的信用利差期限结构，研究表明即使在Merton模型中引入随机利率或进行其它改进，结构模型的信用利差期限结构仍是驼峰形状的。Wei和Guo［9］认为信用利差随期限延伸大致呈现N型。抵押是BaselⅡ标准法规定的信用风险缓释工具之一，但是随着金融全球化进程的加速，现实金融环境的不确定性在增多，抵押交易本身隐含较高风险。因此，含有抵押资产组合的信用风险问题也成为了重要的研究课题。Cossin和Hricko［10］曾利用结构模型方法，分析了抵押资产扣减率和风险抵押对信用风险的影响，考察了风险远期价值等问题。Cossin和Hricko［11］研究了有回购协议时的抵押风险控制问题，最后得到了含有单一抵押资产的模型及抵押损失。

国内学者王志诚［12］应用期权定价理论，考察了基于抵押品的有抵偿贷款信用风险的抵押率及其与贷款利率之间的关系，采用迭代法给出了选定信用利差水平下的平价抵押率。王蕾［13］探讨了抵押、担保对银行信用风险的影响，建立了相应模型并考察了如何能充分发挥抵押、担保对信用风险缓释的作用问题。于晨曦和孙俊波［14］借助一个计量模型和LGD(Loss Given Default)的概念，对抵押品的风险缓释功能进行了理论分析，进而又结合中国商业银行抵押贷款现状的统计结果，分析了当前银行抵押业务中存在的问题。

目前，大多数信用利差模型没有考虑存在抵押时的情况，即使有也只是考察以债券或国债等无风险权益为抵押的单一抵押品问题，并没有建立存在抵押资产组合时的相应模型。而在实际交易中，交易对手往往会提供多种资产的组合作为抵押。抵押资产会影响违约概率的大小，也会影响信用利差期限结构，从而会影响对利率衍生产品的定价。本文基于Merton结构式模型的思想，对公司多种资产抵押信用风险问题建立结构式模型，利用差价欧式期权定价方法，分析在抵押资产组合下零息债券的价格、违约概率及信用利差期限结构的相关特征。

二、抵押资产组合

1.抵押资产组合的设定

抵押可以降低信用风险，在金融市场中被广泛采用。作为抵押的资产可以是单一的抵押品，也可以是抵押资产组合。抵押品本身也存在一定的风险，不同抵押资产组合对信用风险有不同的影响。因此，本文做如下假设:

有两种资产A和B。资产A是交易合同的标的资产，其价值A(t)服从几何布朗运动:

其中，μA是资产A的预期瞬时收益率，σA是资产A的收益率的波动率，是概率空间 (Ω，F，P)上的标准布朗运动，即有

假设公司债券有n个抵押资产，其价值为Mi(t)(i=1，2，...，n)，分别服从几何布朗运动:

其中，μi是抵押资产i的预期瞬时收益率，σi是抵押资产i的收益率的波动率，是在概率空间 (Ω，F，P)上的标准布朗运动。假设各(i=1，2，...，n)和之间的相关系数均为ρ。这些抵押资产的组合为资产B，其价值为B(t)。

其中，Wt表示系统风险，是经济环境中影响所有资产的共同因素;(i=1，2，...，n)和表示非系统风险，表示影响各个资产的不同因素，布朗运动(i=1，2，...，n)、Wt和之间是相互独立的。

关于抵押资产组合的零息债券定价问题。抵押资产组合可有两种方式:几何加权平均和算数加权平均。由于每种抵押资产的价值均服从几何布朗运动，其几何加权平均仍服从对数正态分布，即服从几何布朗运动。这时，关于抵押总资产B的定价可直接采用BS模型方法。如果采用算数加权平均的方式，由于对数正态分布的和已经不再服从对数正态分布，抵押总资产B的定价问题不能直接采用BS模型方法，而且此资产的期权定价得不到解析解。这种情况下，可采用蒙特卡罗数值模拟求解，这会以惊人的时间消耗为代价;如果采用渐近逼近的方法会减少大量时间消耗，因此，对于算术平均组合方式本文采用Gentle［15］的逼近方法。通过变换替代，用几何平均来近似算数平均，从而把两种资产组合方式的期权定价问题统一为都可以采用BS模型方法定价的问题。

2.抵押资产以算数加权平均形式组合

考察这种逼近误差时，分别考虑由2种、4种、10种和20种资产构成的抵押组合进行误差模拟(最长期限为10，初始资产值为50—100)，对每种组合，模拟10 000次。例如，10个抵押资产时最大绝对误差为0.46，最大平均误差为0.16，相对误差全部接近零;20个抵押资产最大绝对误差为6.73，最大平均误差为0.64，相对误差全部接近零。结果表明，随着资产个数的增加，随机因素的增多和确定的指数漂移项都会使绝对误差增大，不过相对于抵押资产组合值的增加来说，相对误差始终接近于零，因此用上述(T)近似B(T)的误差影响可以忽略，而且其时间越短近似程度越好，抵押资产越少近似越精确。为了能更精确地求解期权的价格，相应的敲定价格K可同时变换为K*=K－(E(B(T))－ E((T)))。

3.抵押资产以几何平均形式组合

通过上述分析，对于多个抵押资产的组合如果采用算数平均方式组合，则组合后的抵押总资产价格可很好地近似用几何布朗运动刻画;如果采用几何平均的组合方式，则组合抵押资产价格本身便服从几何布朗运动。因此，抵押组合资产的价格运动轨迹都可以用几何布朗运动刻画。

三、存在抵押时的结构式模型

1.有抵押资产组合时Merton模型的扩展

Cossin和Hricko采用结构式模型方法分析了风险抵押对信用风险的影响，本文采用类似方法分析单边违约与随机抵押组合的信用价差特征，在含有抵押的债券定价问题上扩展Merton模型，并进行相关模拟分析。设标的资产与抵押资产组合的价值分别为A(t)和B(t)，面值为F，到期日为T的零息风险债券的价值如(6)式，其中，r是瞬时无风险利率。

在风险中性假设下，利用价差期权定价的方法可以求解(6)式。一个价差为S1(T)－S2(T)、敲定价格为K≥0、期限为T的欧式看涨期权支付为c(t)=e－r(T－t)Et［(S1(T)－S2(T)－K)+］。max(FB(T)－A(T)，0)可视为S1(T)=A(T)、S2(T)=－B(T)、K=F的看跌差价期权的支付。

2.违约概率

违约概率是度量信用风险的重要指标，直接影响信用利差。在现实概率测度下，当资不抵债时，也就是当A(T)+B(T)＜F时，就说信用违约事件发生。这时F可看做是门限值。按照Merton模型的设定，违约只发生在T时点上，违约概率为P(A(T)+B(T)＜F)。B(t)是各抵押资产的组合，无论是采用几何平均方式还是算术平均方式组合，其运动轨迹都可以近似看做服从几何布朗运动。我们将采用蒙特卡罗法模拟违约概率的分布特征。

本文中各参数选取如下:n=2，ρ=0.20，r=0.06，A(0)=100，M1(0)=40，M2(0)=60，σA=σ1=σ2=0.25，α1=α2=0.50，F=135，T=0.50。利用(5)式生成B(T)，随机生成B(T)和A(T)100 000个，并且模拟10 000次生成B(T)的分布。

模拟结果表明，资产终值分布偏离正态性，其中，偏度为1.99，峰度为5.89。对给定的参数值，其资产终值集中于180左右，较大资产终值和较小资产终值出现的概率都较小，如门限值F=135，模拟的违约概率是0.002，而如果F=180，违约概率接近0.50，不同的违约门限值对违约概率有很大影响。图1给出了对于不同的门限值，违约概率与抵押资产值的关系。其中，F分别取值90、100、110、120，使B(0)值在［0，50］间变化，其余参数选取前面同样数据。当F=90时，在B(0)取值范围内，违约概率几乎接近零(与x轴重合)。当门限值变大时，对于同一个抵押值，违约概率也较大。对于同一个门限值，抵押资产值越大违约概率越小。当抵押值为零时(即无抵押时)，不同门限值决定了违约概率的大小，特别是针对本例半年期的债券，当门限值为100等于资产A(0)时，违约概率达到0.25;而门限值为120时违约概率接近1。实际上，由于要在半年这样短的期限内，市场平均收益0.09和利率0.06时，资产价值达到120几乎是不可能的。

本文模拟分析违约概率与期限的关系时，分别设定门限值为100、110、120，其余参数设定同上，结果如图2所示，门限值越大违约概率越大，随期限的变化违约概率分布呈倒U型;较大门限值对应的分布较凸，且随门限值变小分布变的扁平。值的注意的是，当期限较大时，违约概率不是急速减小为零，而是处于一个稳定值上。

图1 相应于不同门限值的违约概率

图2 违约概率与期限的关系

本文考察抵押初值和相关系数对违约概率的影响时，选取ρ∈［0，1］和B(0)∈［54，70］，其余相关参数同上，模拟结果如图3所示，违约概率随抵押初值的增加而减少;违约概率随相关系数的增加而增大，但增加的幅度较小;如果相关性和初值同时增大，违约概率有显著增大的趋势。因此，只有适当地选择抵押初值和相关抵押资产，才会使违约概率尽可能小。

抵押资产的波动和标的资产的波动会直接影响违约概率。考察资产的波动率对违约的影响，为了简单起见，抵押资产波动率和标的资产波动率分别在(0，1)之间。违约概率与标的资产和抵押资产波动率的动态关系如图4所示。

图3 违约概率与相关系数和抵押值关系

图4 违约概率和标的资产与抵押资产波动率的关系

当抵押资产波动率和标的资产波动率都较低时，违约概率较小(保持常量)。但随着波动率的不断增加，违约概率也相应迅速增大。抵押资产波动率的增加，使违约概率增加得较缓慢;标的资产波动率的增加使违约概率增加得较迅速。因此，标的资产波动率的变化比抵押资产波动率的变化更能引起违约的增加。总之，对于相同的期限，存在抵押资产组合的违约概率要低于无抵押时的违约概率，恰当的抵押资产值会有效降低违约概率，资产相关性的变大增加违约概率。说明了抵押资产组合确实可以缓释信用风险，抵押确实是降低信用风险的一种很好的技术，而且选择抵押品时注意多样性，以降低抵押品的相关性及波动性。

3.存在抵押资产组合时的信用利差

Elton和Collin等给出了信用价差的一种分解，认为价差是由风险溢价、税收和预期损失等因素决定。Driessen认为价差是由风险溢价、税收和流动性溢价等因素决定。为了简化信用价差的分析，本文只考虑风险溢价因素如何决定价差，即信用利差是风险利率与无风险利率的差。

在连续时间情形下，yt(T)为到期日为T、面值为F的债券收益率，其现值为Dt=Fe－y(T－t)。抵押资产价值为B(t)，由(7)式可得信用利差为:

在Merton模型中，如果准债务比大于或等于1，则信用利差随期限递减;如果准债务比小于1，则利差先随期限递增，后又随期限下降，即它的信用利差期限结构是驼峰型的。下面通过数值模拟分析引入抵押资产组合后信用利差期限结构特征。

(1)利差期限结构与相关系数的关系

分别考虑相关系数为正、负两种情形下的利差期限结构。当相关系数为ρ=0.20与ρ=－0.20时，取 n=2， r=0.06，A(0)=100，M1(0)=40，M2(0)=60，σA=σ1=σ2=0.25，α1=α2=0.50，模拟结果如图5所示，实线为负相关系数时的利差，虚线为正相关系数时的利差。

由图5可看出，对不同的资产相关系数，两组期限结构的形状基本相同，但对利差影响较大。相同条件下，一般是正相关系数的利差小于负相关对应的利差，但无论正负，整体上利差会随期限增加趋向于0。本文只在相关系数为正(ρ=0.20)时，模拟出期限和相关系数对利差的影响如图6所示。随着相关系数的增大，利差有增大的趋势，近似为线性趋势;随着期限的增加，利差在减小，并且期限越长利差减小越缓慢。期限对利差的影响要大于相关系数对利差的影响。这表明当存在抵押资产组合时，抵押资产之间的相关性及资产存续期对信用利差期限结构有影响。抵押资产之间相关性越大，利差就越大;随着资产存续期的增大，利差在减少。

图5 相关系数为正和负时不同面值F对应的期限结构

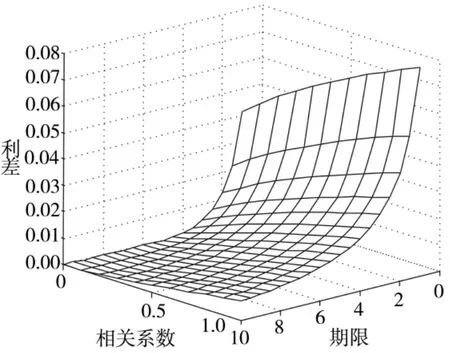
图6 相关系数与期限对利差的影响

(2)多个抵押资产组合与单个抵押资产的比较

含有抵押资产组合时，由于抵押品可以分散风险，其违约概率变小。这里考察单个抵押资产和多个抵押资产对利差结构的影响，为了便于比较，设两种情况下的抵押资产价值相同。对多个抵押资产，采用参数同前文，单个资产中只取M1(0)=50，M2(0)=0，其余相同。单个资产模拟结果如图7所示，多个资产模拟结果如图5虚线部分。

比较图7和图5可以看出，整体上单个抵押资产下的信用利差明显小于抵押资产组合时的信用利差;同时随着期限的不断增加，单个抵押资产对应的利差下降快，趋向零的速度显著变快。但是两种情形下其利差值要比相同条件下无抵押的Merton模型的利差值要小。

当单一抵押品的初始资产价值大于抵押资产组合的初始资产价值时，其信用利差小于抵押组合下的信用利差;当单一抵押初始资产价值小于抵押资产组合的初始资产价值时，其信用利差大于抵押组合下的信用利差。这是由于抵押资产组合的抵押风险可能会大于也可能会小于单一抵押时的抵押风险，为使信用风险变小，就要选择合适的抵押资产组合，使得在抵押资产组合下的信用风险要比单一抵押品时的信用风险和无抵押时的信用风险都要小。

(3)抵押资产为无风险债券时的利差

考虑抵押资产为无风险债券时，令σ1=σ2=0，其余参数同上，模拟结果如图8所示，实线为无风险抵押资产组合的利差，虚线为风险资产组合的利差。

图7 单个抵押资产时利差期限结构

图8 抵押为无风险和风险债券时的信用利差期限结构

(4)标的资产波动和抵押资产波动对信用利差的影响

图9 标的资产波动率和抵押资产波动率对利差的影响

资产价格的波动率反映了资产价格的不确定性。下面分析标的资产波动率和抵押资产波动率如何影响信用利差。为了分析简单，设资产价值波动率在［0，1］之间，抵押资产波动率在［0.2，1］之间，其余参数同上，模拟结果如图9所示。与抵押资产的波动和标的资产的波动对违约概率的影响类似，随抵押资产波动、标的资产波动的增大，信用利差也增大。标的资产波动率的增加使信用利差增大较快，而抵押资产波动率增加使信用利差增大较慢。因此，为了分散风险，在选择抵押资产组合时要注意选取波动率较低的资产组合搭配，以降低信用风险。

四、结束语

抵押是将信用风险转化为市场风险，从而分散并降低信用风险。本文利用结构式模型思想，构建了含有抵押组合的信用风险模型。研究表明，它能准确地刻画风险零息债券的价格变化，描述违约概率、风险利差的动态行为，这将有助于我们理解信用风险、利率产品定价风险。本文得出以下主要结论:第一，违约概率分布是非正态的。违约概率与门限值有很强的非线性递增关系，而违约概率和资产组合值呈现递减关系，门限值、标的资产价值、抵押资产价值及其波动可以明显地影响违约概率的大小。相关系数的正负性不影响信用利差曲线形状，但影响利差大小。各种资产间的相关性越大，会导致利差越大，从而带来较大风险。因此，选择抵押资产时，应关注各资产间的相关程度及违约门限值的设定。第二，当存在抵押资产组合时，零息债券的信用利差要小于无风险时的信用利差，并且有抵押时违约概率要小于无抵押时的违约概率，这说明抵押确实可以缓解信用风险。抵押资产组合的信用利差大于单一抵押资产下的利差，这要求精确选择资产组合，使得降低信用风险的同时可以降低利差风险。第三，当不存在抵押时，结构式模型的信用风险利差期限结构是驼峰型的，在加入抵押资产组合后，信用风险利差期限结构变为L型曲线。

［1］ Merton，R.C.On the Pricing of Corporate Debt:The Risk Structure of Interest Rates［J］.Journal of Finance，1974，29(3):449－470.

［2］ Jarrow，R.A.，Turnbull，S.M.Pricing Derivatives on Financial Securities Subject to Default Risk［J］.Journal of Finance，1995，50(1):53－86.

［3］ Duffie，D.，Singleton，K.Modeling the Term Structure of Defaultable Bonds［J］.Review of Financial Studies，1999，12(4):687－720.

［4］ Jarrow，R.A.，Protter，P.Structural versus Reduced－Form Models:A New Information Based Perspective［J］.Journd of Investment Management，2004，2(2):34－43.

［5］ Leland，H.，Toft，K.B.Optimal Capital Structure，Endogenous Bankruptcy，and the Term Structure of Credit Spreads［J］.Journal of Finance，1996，51(3):987－1019.

［6］ Chen，N.，Kou，S.G.Credit Spreads，Optimal Capital Structure，and Implied Volatility with Endogenous Default and Jump Risk［J］.Mathematical Finance，2009，19(3):343－378.

［7］ Longstaff，F.，Schwartz，E.A Simply Approach to Valuing Risky Fixed and Floating Rate Debt［J］.Journal of Finance，1999，54(3):789－819.

［8］ Sarig，O.，Warga，A.Some Empirical Estimates of the Risk Structure of Interest Rates［J］.Journal of Finance，1989，44(5):1351－1360.

［9］ Wei，D.G.，Guo，D.Pricing Risk Debt:An Empirical Comparison of the Longstaff and Schwartz and Merton Models［J］.The Journal of Fixed Income，1997，7(2):9－28.

［10］ Cossin，D.，Hricko，T.Pricing Credit Risk with Risky Collateral:A Methodology for Haircut Determination［R］.Working Paper，HEC，University of Lausanne，1999.

［11］ Cossin，D.，Hricko，T.A Structural Analysis of Credit Risk with Risky Collateral:A Methodology for Haircut Determination［J］.Economic Notes，2003，32(2):243－282.

［12］ 王志诚.用期权定价原理分析抵押贷款的信用风险［J］.金融研究，2004，(4):95－105.

［13］ 王蕾.抵押、担保对银行信用风险因子的影响机制研究［J］.统计与决策，2007，(24):124－126.

［14］ 于晨曦，孙俊波.商业银行抵押风险分析［J］.金融论坛，2008，(1):41－47.

［15］ Gentle，D.Basket Weaving［J］.Risk，1993，(6):51－52.

［16］ Safak，A.Statistical Analysis of the Power Sum of Multiple Correlated Log-Normal Components［J］.IEEE Transactions on Vehicular Technology，1993，42(1):58－61.

［17］ Kirk，E.Correlation in the Enerqyenery Markets，in Managing Energy Price Risk［M］.London:Risk Publications and Enron，1995.71－78.

［18］ Elton，E.J.Explaining the Rate Spread on Corporate Bonds［J］.Journal of Finance，2001，56(1):247－277.

［19］ Collin，D.P.，Goldstein，R.，Martin，S.The Determinants of Credit Spread Changes［J］.Journal of Finance，2001，56(6):2177－2208.

［20］ Driessen，J.Is Default Event Risk Priced of Corporate Bonds?［J］.The Review of Financial Studies，2005，18(1):165－196