高速可配RSA加速器设计与实现*

曾健林，黄 凯，马 德，冯 炯，葛海通，严晓浪

（1．浙江大学超大规模集成电路研究所，浙江杭州 310027;2．杭州市中天微系统有限公司，浙江 杭州 310012）

0 引言

随着现代通信和计算机网络的快速发展，公钥基础设施（public key infrastructure，PKI）成为信息安全领域不可或缺的一部分。作为PKI重要一部分，RSA［1］算法得到了广泛的关注。RSA算法是在1978年由Rivest R，Shamirh A和Adleman L提出的一种非对称加解密算法。RSA的安全级别与密钥长度呈正比，而运算复杂度也相应加大。当前不同的应用迫切需要根据安全和成本需求来采用不同长度的密钥，并具备高速的加解密性能。然而，传统的纯软件实现方法虽具备高度的灵活可配型，但远远不能满足高速RSA加解密应用需求。因此，设计密钥长度可配置的高性能RSA硬件加速器已逐渐成为一个重要的研究方向。

RSA算法的实质是大数的模幂运算，可以通过多次模乘循环实现。虽然RSA加密算法具有很高的安全性，但由于模乘运算的复杂性，RSA的运算速度始终成为制约RSA广泛应用的瓶颈。RSA硬件加速器可以显著提高RSA的运算速度，但模乘运算中包含着多次加法、减法和除法迭代运算，VLSI实现具有很高的代价。当前，RSA硬件设计的相关研究主要集中在模乘算法的改进和高效的VLSI实现2个方面。蒙哥马利模乘［2］（Montgomery modular multiplication，MMM）算法被认为是最高效的模乘算法，利用MMM算法，RSA可以通过简单的移位和加法实现，这使得VLSI实现变得可行。文献［3，4］提出了基于MMM算法的RSA协处理器，但运算并行度不高，导致数据吞吐率较低。

本文采用基—64MMM模乘算法来实现RSA加解密运算加速器，通过五级流水线架构的模乘器和高度并行可配架构的存储器，可支持不同长度的密钥，并显著地提升了运算效率，取得了较好的性能和硬件资源消耗比。

1 算法描述

1．1 Montgomery算法的描述

MMM算法由Montgomery P L在1985年提出，提供了一种快速计算A×B×R－1mod N的方法，通过一定的预运算和后运算得到真正形如S=A×B mod N模乘运算结果。它采用模加和右移的方法，避免了通常求模算法中费时的除法操作。

算法1为原始的MMM算法，其中A，B为任意2个整数，N为模数且N＞1，R为满式（1）的一个基（通常取R为2n，n为输入大数的位数）

R－1和N'为满足式（2）和式（3）的正整数

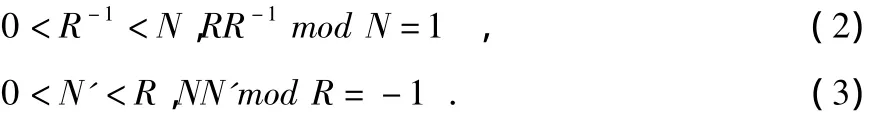
算法 1:function MMM（A，B，N）{

算法1中每次模乘运算总有A×B和M×N两次大数运算，对于2048位 RSA，A，B和M可能是2048位的大整数，大数乘法的硬件实现仍然具有很大的代价，因此，Montgomery提出了改进的算法，取r=2w称为基，w为字长，大整数A，B，N表示如下

此时式（3）相应的为

改进的MMM算法通过循环的办法，分多次来完成大数的运算，比算法1更利于硬件的实现。

1．2 MMM—64 算法

目前，大多数模乘运算的硬件结构都基于改进的MMM算法。文献［5］在改进的MMM算法基础上取基r为2得到基2—MMM算法，然后采用脉动阵列实现模乘运算。但基—2的MMM算法运算并行度不高，会导致整体的运算效率较低。为了提高运算并行度，需要采用高基的MMM算法。

现提出一种适合硬件实现的基—64MMM算法。算法描述如下

算法 2:function MMM_64（A，B，N）{

可以看出:上述基—64MMM采用64位的乘法运算和加法运算，极大地提高了运算并行度，可以充分利用硬件的运算能力，提高效率。同时，该算法对可支持的运算长度没有限制，通过控制循环次数k实现了运算长度的可配。

1．3 基于MMM的RSA算法

MMM算法实现的只是A×B×R－1mod N，可提供了解决模乘甚至是模幂运算的新的方法。经过适当的预处理，循环运算以及反处理，可以得到形如AEmod N的结果。算法如下:

将幂数E展开成二进制形式，形如E=（ew，ew－1…ei…e1，e0）2，通过从左到右遍历E的每一位，来实现模幂运算。

算法 3:function RSA（A，E，N）{

其中，P=R2mod N只需运算一次，且仅与R和N有关，故可由软件来完成。从上述算法可知，模幂运算可由多次MMM算法来完成。对于N位的RSA运算，在最差情况下，E的每一个二进制位都为1，需要（2N+2）次MMM运算;在平均情况下，E的二进制表示中“1”的期望值为N/2，需要（1．5N+2）次MMM运算。

2 RSA硬件架构设计

2．1 整体架构

RSA加速器整体架构如图1所示，主要由AHB接口、寄存器组、存储区、控制器和模乘器5个部分组成。

AHB接口模块是加速器总线交互的接口，处理器运行完预处理的软件操作后，可以通过AHB接口配置或读取加速器的内部寄存器组和存储器。

寄存器组是用来存放一些控制信息和状态信息，如支持不同长度密钥模式的配置等。存储区是用来存放RSA运算所需的密钥和运算数据等信息。

控制器通过状态转换控制模乘器的运算。由算法3可知，RSA运算可由多次模乘迭代运算完成。需要注意的是，每一次模乘运算输入与输出不尽相同，数据将在模乘器和存储区之间频繁的流通。控制器将完成不同MMM运算的调度，保证存储区提供正确的数据给模乘器，同时保证模乘器的输出存放到正确的存储区。

模乘器是运算的主体，承担基—64MMM算法。

图1 加速器架构Fig 1 Architecture of accelerator

2．2 模乘器流水线架构

基—64MMM算法中，涉及2个64位的乘法运算，为了使系统能够运行在较高的频率，提高系统吞吐率，采用带流水级的乘法器来实现。同时，由于2个乘法运算没有数据依赖性，可以并行的运算，进一步提高性能。模乘器流设计如图2所示。

图2 模乘器结构Fig 2 Architecture of modular multiplier

在乘法器的选择上，需要综合考虑流水级深度和硬件资源，前者直接关系到运算性能，后者则关系到实现代价。MUL2为一个两级流水的乘法器。这个乘法器将承担T［i］的计算。算法2可知，这一过程需要2个乘法运算，并且这2个乘法运算具有数据依赖性，只能依次完成。因此，乘法器每增加一级流水，就相当于需要额外增加2个周期的等待时间。故牺牲一部分面积，采用一个两级流水的乘法器，以提高性能。得到的T［i］将存储在寄存器T中。同时这个乘法器还将承担流水级中ai×bj的运算。这个乘法器为流水线的前两级。第三级流水为加法级，完成cj的累加。MUL3为一个三级流水的乘法器，将承担T［i］×bj的运算，既匹配了流水线，实现了并行运算，又节省了一部分面积。第四级也为加法级，将MUL3的结果与前三级的结果相加。第五级为进位和写回级，运算结果将直接写回存储区，同时产生进位给下一次运算。所用的加法器同时将承担C-N的运算。

模乘器的设计，综合考虑了高的性能和低的硬件资源消耗。合适的流水深度保证了高的数据吞吐率。完成N位的模乘运算仅需M=N/64×（N/64+5+4）个时钟。

2．3 存储结构

在运算过程中，模乘器需要同时读入3个64位的数据（cj，bj，nj），写出一个 64 位的数据（cj－1），对数据带宽要求很高。同时，从RSA运算的整体来看，这些数据需要频繁的读取和写入，因此，这里考虑在加速器内加入存储区域，以方便数据的并行访问。存储结构如图3所示。

图3 存储结构Fig 3 Architecture of memory

这个存储器由5块单端口SRAM组成，每一块的数据宽度为64位，可实现并行访问。其中，第一块存储模数N;第二块分成3个区间，分别存储密钥E，预处理辅助参数P和待加密数A;第三，四和五块用来存储运算中间值和运算结果。如图4所示，存储器的大小由密钥的长度需求来决定。在低端应用中，可以通过将存储器配小，节省硬件资源。在高端应用中，可以通过增加存储器来支持长达2048 bit位的RSA运算。同时，大配置的存储器能够兼容低端的应用，可以通过配置寄存器组中相关的寄存器来完成不同长度的RSA运算。这样就从硬件和软件2个方面实现了加速器的可配性。可配存储器大小如表1。

在运算过程中，N，E，P的值是保持不变的，MMM（A，P，N）运算后，A会更新为A'。在 MMM（B，B，N）运算中，M0，M1，M2将分别提供cj，bj读取以及cj－1写入，保证了模乘器的数据供给和写出，流水线可以不阻塞的工作。

表1 可配存储器的大小Tab 1 Size of configurable memory

3 实现与比较

本文采用Verilog HDL语言实现了采用基—64MMM算法五级流水模乘器的RSA硬件加速器RTL代码。对于N位的RSA运算，完成一次模乘所需时钟数为M=N/32×（N/64+5+4）;最差情况下，完成一次模幂运算所需时钟数为（2N+2）M，而在平均情况下，完成一次RSA运算所需时钟数为（1．5N+2）M。在存储结构最大支持2048位RSA运算情况下，采用SMIC0．18 μm工艺库综合后，在最差条件下，加速器可以运行高达200 MHz，所需硬件资源为73 k门和1792 byte SRAM，各模块所需资源如表2所示。

表2 各模块硬件资源Tab 2 Hardware resource of each module

表3是本文所实现的模乘器与其他文献的性能对比。可以看出:本文实现的模乘器所需时钟数节省了约50%。

表3 模乘器性能对比Tab 3 Performance comparison of modular multiplier

表4是RSA硬件加速器的性能对比。本文所设计的RSA硬件加速器，在硬件资源消耗差别不大的情况下，实现了2～3倍的数据吞吐率，达到了较好的性能资源消耗比。

表4 RSA硬件加速器性能对比Tab 4 Performance comparison of RSA hardware accelerator

4 结束语

本文采用一种利于硬件实现的基—64MMM算法，实现了高速可配的RSA硬件加速器。该加速器通过五级流水线模乘器及对应的并行存储结构，显著提高了RSA运算性能，并支持不同密钥长度的高度可配性。与相关工作比较，具有较好的性能资源消耗比。

［1］ Rivest R L，Shamir A，Adleman L．Method for obtaining digital signatures and public key cryptosystems［J］．Communications of the ACM ，1978 ，21（2）:120 －126．

［2］ Montgomery P L．Modular multiplication without trial division［J］．Mathematics of Computation，1985，170（44）:519 －521．

［3］ Zheng Xinjian，Liu Zexiang ，Peng Bo．Design and implementation of an ultra low power RSA coprocessor［C］∥The 4th International Conference on Wireless Communications，Networking and Mobile Computing，WiCOM 2008，2008:1 －5．

［4］ Liu Jizhong，Dong Jinming．Design and implementation of an efficient RSA crypto-processor［C］∥2010 IEEE International Conference on Progress in Informatics and Computing（PIC），2010:368 －372．

［5］ 蒋晓娜，段成华．改进的蒙哥马利算法及其模乘器实现［J］．计算机工程，2008，34（12）:209 －211．

［6］ Huang Miaoqing，Gaj K，Kwon S，et al．An optimized hardware architecture for the Montgomery multiplication algorithm ［J］．Public Key Cryptography（PKC），LNCS，2008，4939:214 －228．

［7］ 王缔郦，白国强，陈弘毅．一种 Montgomery模乘算法硬件结构［J］．微电子学与计算机．2010，27（5）:1 －4

［8］ Chen Yunlu，Tseng Chihyeh，Chang Hsiechia C．Design and implementation of reconfigurable RSA cryptosystem［C］∥International Symposium on VLSI Design，Automation and Test，2007:1 －4．