光电经纬仪对心偏差引起的方位测角误差补偿方法
2012-10-22蒲鹏程郭晓松周召发郭君斌
蒲鹏程,郭晓松,周召发,郭君斌
(第二炮兵工程学院,陕西西安 710025)
0 引言
经纬仪对心偏差的存在直接影响其测角精度,目前有多种方法实现经纬仪对心[1],大体可分为两类:第一类方法有垂球对心、光学对心、激光对心等,此类方法优点是流动性大,但对心精度都不太高,最优为0.5 mm。强制对心是另外一类对心方法,一般和观测墩结合,通过在观测墩上预留螺纹或精密轴套,实现仪器的精密对心,其优点是对心精度高,一般优于0.05 mm,对心速度较快;缺点是不太灵活、比较复杂、需建观测墩。上述方法存在的主要问题包括:自动化程度低、操作时间长、精度受参考基准指示器的精度和人眼判读误差的限制[2]。随着微电子技术不断发展和对经纬仪误差理论研究的不断深入,软件补偿的方法[3]由于具有方法灵活、易于变动、成本低等特点,在经纬仪误差处理中得到广泛的应用,取得了很好的效果。本文根据这一误差设计理念,利用计算机视觉技术来检测对心偏差,提出通过软件补偿的方法来修正对心偏差对方位测角影响。
1 经纬仪对心偏差引起的方位测角误差分析
如图1所示,设∠CBA为正确的角度值,但在实际测量时,仪器架设中心D与实际地标中心B存在对心误差e,因此,实际测得的角度为∠CDA,存在测角误差:δ=∠CDA-∠CBA。作BD的延长线于E点,则有

为了消除对心偏差对方位测角误差的影响,本文提出了基于计算机视觉的误差补偿方法,该方法通过在经纬仪下方安装CCD摄像头,实时检测出对心偏差的大小和方向,并根据经纬仪的读数,计算对心偏差引起的测角误差值,对测量结果进行实时修正,得到正确的角度值,从而实现不精确对心条件下的方位角精确测量。

图1 光电经纬仪对心偏差引起的方位测角误差示意图Fig 1 Azimuth measurement error by centering deviation of photoelectric theodolite
2 对心偏差引起的方位测角误差补偿方法
2.1 经纬仪架设中心在CCD图像中位置关系的标定
将CCD摄像机固连在经纬仪照准部下方,经纬仪调平后,通过合理安装,尽量使摄像机的成像平面是一个水平面,这样CCD摄像机的成像平面与经纬仪相对位置固定,保证经纬仪与CCD图像坐标的位置标定后不会发生改变。
在标定场地中有A,B两点,将经纬仪、标杆仪调平,并分别精确架设于B,A两点。
利用经纬仪下方固连的CCD摄像头检测地标B在图像中的坐标,如图2中B'(xd,yd),该坐标代表经纬仪竖轴铅锤时在地面上的投影在CCD成像中的位置,从而完成经纬仪架设中心在CCD图像中位置关系的标定。

图2 定标过程视准轴所在直线在图像中的成像关系Fig 2 The line represented for collimation axis in CCD image in the process of emendation
但由于加工工艺等因素的限制,成像平面不可能完全水平,即此时CCD成像光轴会与竖轴存在一个微小夹角,这样经纬仪架设中心标定就会存在误差,需要校正。传统采用对心镜方式对心时需要拆开经纬仪进行硬件校正,校正难度大。而采用CCD检测对心偏差方式就可以很好地解决这个问题,架设经纬仪于B点,将经纬仪旋转一周,如果CCD成像光轴与竖轴存在夹角,那么B点成像点会分布在一个圆上,将所有B像点坐标拟合得到一个圆,该圆圆心即为经纬仪竖轴铅锤时在地面上的投影在CCD成像中的位置,从而消除CCD成像光轴与竖轴不重合的影响,完成经纬仪架设中心在CCD图像中位置关系的标定。
2.2 经纬仪望远镜视准轴在CCD图像中位置关系标定
经纬仪瞄准标杆仪,并记录水平度盘读数ε,过A,B中心,拉一根直细线(代表视准轴方向),利用经纬仪下方固连的CCD摄像头检测出直线,如图2,AB所成图像A'B'与图像坐标x轴所成的角Ф,即为此时经纬仪视准轴与图像坐标x轴的夹角,则度盘读数为零时视准轴方向与图像坐标x轴的夹角为Ф-ε,从而完成经纬仪望远镜视准轴在CCD图像中位置关系标定。
2.3 误差补偿模型建立
假设经纬仪测角时检测到的地标中心在图像中的坐标为B'(x1d,y1d),由2.1节可知,架设中心D成像坐标为D'(xd,yd),如图3所示,则经纬仪架设偏差DB的方向就可以用D'(xd,yd)与B'(x1d,y1d)的连线确定。
同时利用图像坐标到实际坐标的转换矩阵H将(xd,yd),(x1d,y1d)转换到实际坐标(Xd,Yd),(X1d,Y1d)
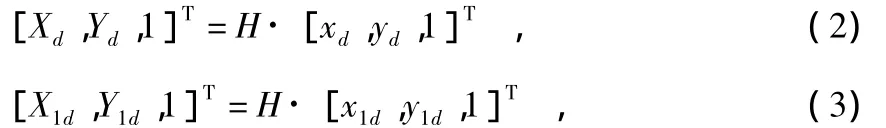
则对心偏差大小


图3 测角过程视准轴所在直线在CCD图像中的成像关系Fig 3 The line represented for collimation axis in CCD image in the process of measureing angle
在实际测角过程中,架设点D分别与点C、点A的精确距离LDC和LDA,可以通过经纬仪测得。假设瞄准C点时水平度盘的读数为γ1,DC就是视准轴的方向,因此,DC所在直线在图像平面中的投影D'C'与图像平面的x轴所成的角为Φ-ε+γ1,如图3所示。同理,假设瞄准A点水平度盘的读数为γ2,则DA所在直线在图像平面中的投影D'A'与图像平面的x轴所成的角为Φ-ε+γ2,由于D'B'方向已知,因此,在成像平面可以确定∠C'D'B'和∠A'D'B'大小β1,β2,又因为成像平面与地面平行,则∠CDB和∠ADB大小分别为 β1,β2。同时假设∠DCB和∠DAB大小分别为δ1,δ2,则根据公式(1)有 δ= δ1+ δ2。
因此,在图1△BDC中,由正弦定理得

所以,有

在实际测量过程中由于e远小于LBC和LDC,且δ1为小角度,故LBC≈LDC,δ1≈sinδ1,公式(6)可写成

同理,在△BDA中,可得

由公式(7)、式(8)可以求出测角误差δ

通过上述模型,可在经纬仪测角过程中,快速计算出存在对心偏差时测角误差值,实时对测量结果进行补偿,从而实现经纬仪非精确对心条件下的精确测角。
3 补偿模型精度分析
通过补偿模型虽然能实现光电经纬仪精确对心条件下的方位角测量,但模型精度能否满足经纬仪高精度测角的要求,还需要作进一步的分析。
由于式(7)、式(8)具有相同的结构,故其误差影响规律也相同,因此,为了便于分析,可以对补偿模型公式(9)作如下简化

其中,e为对心偏差,β 代表 β1或 β2,L代表LDC或LDA,分别用来分析CCD图像检测精度、经纬仪测距精度对补偿模型精度的影响规律。
根据误差分配原理[4],可将补偿模型的误差Δδ表示成如下形式

其中,Δe,ΔL和Δβ分别为CCD检测对心偏差的检测误差、模型求解L和β1或β2时的求解误差。将式(10)代入式(11)可得
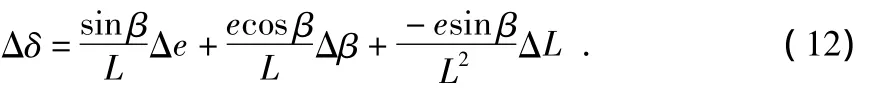
由于|sinβ|≤1,|cosβ|≤1,因此

在光电经纬仪实际测量过程中,对心偏差可以很容易控制在10 mm以内,即e≤0.01 m。经纬仪测角时距离目标一般大于30 m,即可假设L≥30 m。
由2.2,2.3节分析可知Δβ有两部分构成:经纬仪固有的测角误差和 CCD检测直线的定位误差。由于e/L≤10-3,因此,经纬仪固有的测角误差对模型误差的影响可以忽略不计,由于图像测量定位精度[5~9]高于 10 μm,CCD 检测直线的角度定位精度高于 0.02°,即可取 Δe=10 μm,Δβ =0.02°。
ΔL由两部分组成:经纬仪测距误差[9](表示为:±2 mm±2×10-6×L)和模型取LBC≈LDC简化时的近似误差。由图1可知,LDC-e≤LBC≤LDC+e,即近似误差为e,因此,ΔL=0.02+2 ×10-6L+0.01。
将 Δe,Δβ,ΔL,L带入式(13)有
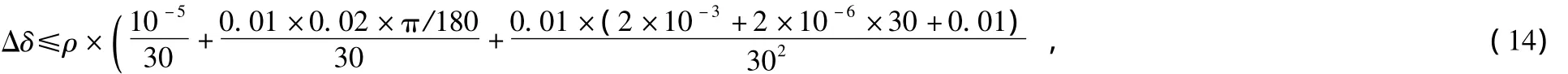
并得:Δδ≤0.12″。其中,ρ为弧度到角度秒的换算关系:ρ=1/π ×180 ×3600=2.06 ×105″。
即误差补偿模型精度完全能满足经纬仪高精度测角要求。同时本文研究了测量目标距离对测角误差的影响,如表1。

表1 测量目标在不同距离时的测角误差Tab 1 Measuring angle error of different distance
可以看出:模型补偿的方法相比传统对心方法,在目标距离相同时,方位测角精度更高,而且强制对心(对心偏差0.05 mm)方法由于需要建立专门的观测墩,测量方式不灵活,而其他对心方法对心偏差最优只能达到0.5 mm,因此,为了保证一定的测角精度,则要求目标距离足够大,这就提高了对测量场地的要求。而模型补偿的方法在较短距离测角时也能满足精度要求。另外,不同于传统对心方式需要精确架设经纬仪,采用补偿模型的方法允许经纬仪架设中心偏差10 mm,很容易完成,大大缩短了操作时间。
4 结论
基于计算机视觉的误差补偿方法,通过在经纬仪下方安装CCD摄像头,实时检测出对心偏差的大小和方向,利用建立的误差补偿模型对对心偏差引起的方位测角误差进行补偿,并且对CCD可能存在的安装误差提出了校正方法,最后对补偿模型精度进行了分析,结果表明:模型精度满足经纬仪高精度测角要求,从而实现不粗对心条件下的方位角精确测量。该方法在保证经纬仪测角精度的同时,提高了经纬仪方位测角的自动化程度,缩短了操作时间,并且降低了对测量场地的要求,测量方式更加灵活,特别适合于小场坪粗对心的快速测角,对军用导弹瞄准及近距离快速测角、民用经纬仪高精度测量等都有一定的理论和工程应用价值。
[1] 于成浩,柯 明,赵振唐.论测量仪器的精密整平及对中技术[J].测绘科学,2006,31(6):87 -88.
[2] 刘春桐,何祯鑫,赵晓枫,等.经纬仪的调平对心误差补偿研究[J].兵工自动化,2010,28(3):249 -252.
[3] 叶晓明,凌 模.全站仪原理误差[M].武汉:武汉大学出版社,2004:20-30.
[4] 费业泰.误差理论与数据处理[M].北京:机械工业出版,2002.
[5] 江 晓.图像测量技术及其应用研究[D].厦门:厦门大学,2008.
[6] 李 婧.图像测量技术中的若干问题研究[D].西安:西安电子科技大学,2007.
[7] 于新瑞,王石刚,王高中,等.数字图像直线特征的亚像素位置检测[J].光学技术,2004,30(2):138 -141.
[8] 何祯鑫.经纬仪自动调平对心系统总体设计及关键技术研究[D].西安:第二炮兵工程学院,2010.
[9] 滕今朝,邱 杰.利用 Hough变换实现直线的快速精确检测[J].中国图像图形学报,2008,13(2):234 -237.
