MEMS陀螺仪零位误差分析与处理*

陈旭光，杨 平，陈 意

(电子科技大学机械电子工程学院，成都 611731)

微电子机械系统MEMS(Micro-Electro-Mechanical System)陀螺仪以其尺寸小、质量轻、价格低的优点越来越受到人们的重视，但是精度较低限制了它的应用领域。提高MEMS陀螺仪精度主要方法有提高加工工艺的精度和对陀螺仪的误差做精准的补偿两种方法，前者的周期较长且易于增加成本，而后者则是一种目前比较可行的方法。MEMS陀螺仪的误差主要包括零位误差和动态误差，一般重点对零位误差做处理［1－2］。零位误差又分为零值偏移误差和随机漂移误差，目前对MEMS陀螺仪零位误差的估算方法主要包括1σ和Allan方差两种方法。1σ方法得到的是误差的总体指标，Allan方差分析法可以对误差的各种成分进行有效的分析［3－7］。目前对零值偏移误差的补偿方法比较简单，一般采用在静态条件下测定零值偏移常量，在应用中通常采用对其一次性的零值偏移补偿的方法。在陀螺仪长时间工作以及外界环境发生变化条件下，零值偏移量并非恒定值，所以这种简单的零值偏移误差补偿方法存在很大的缺陷［8］。对陀螺仪的随机漂移误差补偿目前常采用Kalman滤波的方法，因这种方法具有较好的实时性得到了广泛的引用，但是Kalman滤波法要求信号必须是平稳时间序列，且要知道信号的激励噪声和观测噪声的方差［9－10］，在实际应用中这两种方差较难测得。

鉴于此，本文从工程应用的角度出发，详细阐述了基于Allan方差的陀螺仪的零位误差分析法、动态零值偏移误差的补偿方法以及基于 HDR［11－12］的随机误差补偿法，旨在对如何对陀螺仪的误差进行分析和处理提供一种新思路和技术参考。

1 MEMS陀螺仪误差分析

Allan方差分析法是对陀螺仪误差分析中通常所采用的方法，该方法不仅能综合分析陀螺仪的性能，还可以得到陀螺仪的各项静态误差指标。

1.1 Allan方差分析法的基本原理

假设采样时间间隔为Ts，总的采样时间为T，那么就可以得到总数据点数为N=T/Ts的一个数据样本，接下来就可以按以下步骤来构造 Allan方差曲线:

(1)按时间顺序将数据均分为K个子集，每个子集的数据点数为n，每个数据子集的平均时间为τ(n)=nTs。

(2)每个子集的均值可以用下式表示。

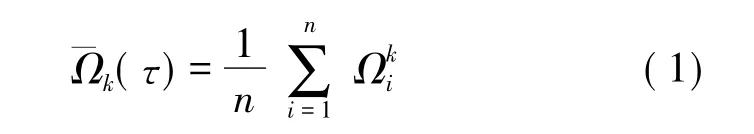
(3)每个不同的子集之间的方差即为Allan方差可以表示为式(2)。

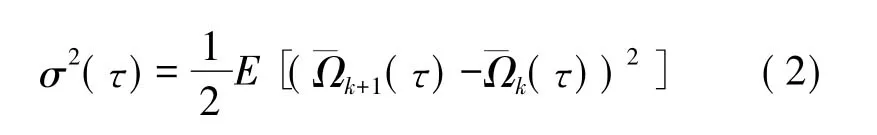
式中σ2(τ)表示平均时间为τ时的Allan方差，E表示求均值。

(4)以平均时间τ为自变量，就可得到Allan方差随平均时间τ变化的曲线图，再经对数变换便可到用来做误差分析的Allan双曲线图。几种常见的误差对应不同的平均时间，也就是对应双对数曲线的不同斜率。表1列出了常用的3种误差系数与Allan方差的对应关系，通过这种对应关系就可以确定3种噪声的系数。

表1 Allan标准差与常见的误差系数对应的关系

1.2 MEMS陀螺仪误差分析

对陀螺仪采集数据前，先让陀螺仪预热一段时间，保证陀螺仪工作稳定后，以100 Hz的采样频率进行采样，采样时间为3 h。得到数据后以MATLAB为数据处理平台进行数据处理，图1为计算所得Allan方差双曲线图。

将Allan方差曲线经多项式拟合后求取相应的斜率值，便可得到的各噪声系数如表2所示。从表中可以看出量化噪声系数很小，这说明数据采集系统的精度符合要求；角度随机游走系数较低表明驱动和检测模态稳定性较好；但是零值偏移不稳定系数较大，这说明零值偏移误差的稳定性较差，这要求在以后的滤波和补偿中不能简单的一次性补偿零值偏移误差，本文提出的动态零值偏移补偿算法能很好的解决这一问题。

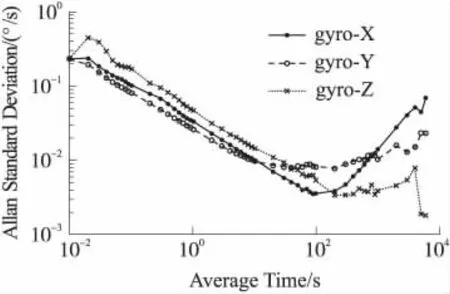
图1 陀螺仪数据Allan方差分析图

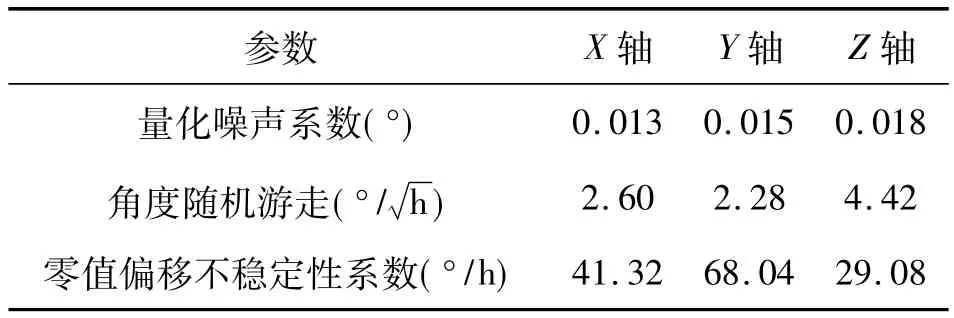
表2 MEMS陀螺仪噪声系数

2 零值偏移误差补偿

一般地对零值偏移误差的补偿都比较简单，通常采用陀螺仪工作稳定后一段静止数据的均值来补偿陀螺仪在整个运行过程中的零值偏移误差，但是随着陀螺仪的工作时间的增加、环境温度的变化等因素的影响，陀螺仪的零值偏移也会产生明显的漂移。

图2为经过滤波后的陀螺仪静态漂移信号，从图中可以看出2 h后的零值偏移发生了明显的漂移，并且有进一步增大的趋势，在这种情况下，若只采用固定的均值补偿很难准确的消除零值偏移误差的影响，这将给导航角的计算带来很大的累积误差。为了能更为准确的去除零值偏移误差，本文提出了一种动态的补偿方法，其程序流程如图3所示。

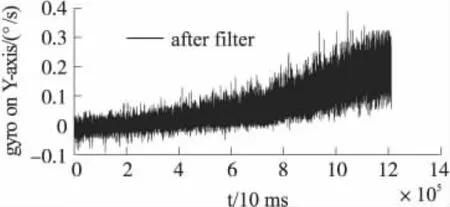
图2 滤波后静态信号

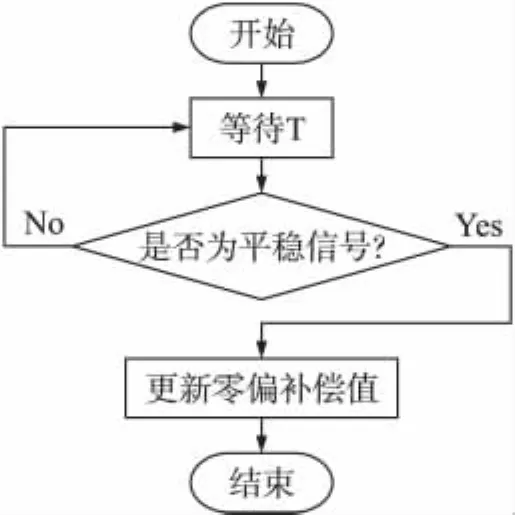
图3 动态补偿零值偏移流程图

首先算法预先设定零值偏移补偿因子的更新时间T。T的值越大补偿算法的实时性将变的越差，如果T值太小计算量就明显增加，一般选择在10 min左右。设定更新时间T后，算法就以T为时间间隔对补偿因子进行更新。载体有角速度输入时，陀螺仪输出信号为非平稳信号，当载体为静止或为直线运动情况下陀螺仪信号为平稳信号，这时对陀螺仪的输入才为零。所以更新补偿因子前算法首先判定当前信号的平稳性，若当先信号为平稳信号，便可取当前的一段数据的均值来更新补偿因子，若当前信号为非平稳信号，则应跳过此次更新。实际应用中选用分段检验法判定信号的平稳性［13］。

3 随机漂移误差补偿

假定载体在运动过程中若不是在转弯则是在沿直线运动，那么理论上陀螺仪的输出应该为零，若不为零则将之视为随机漂移。HDR算法就是根据以上理论得到启发，先判定载体是否沿直线运动，若是则对陀螺仪的输出进行补偿。

从图4可以看出，HDR算法其实是一个闭环的控制系统，这也是这种算法和其他的误差处理算法的不同之处。陀螺仪输出信号主要有wtrue、ε0和εd组成。wtrue为真实的输入值，也是最终要测的量，为了能测得准确的wtrue值，就必须从测得数据中将ε0和εd除去。其中零值偏移量ε0的补偿已经在第二部分中讲述。若输入的角速度为0，对ε0进行补偿后陀螺仪的输出仅为随机漂移εd，从控制系统的角度理解，εd为干扰，如果参数选择合理，在稳定状态下，通过比例积分或者仅通过积分环节，系统可以收敛于0，这就意味着控制信号可以无偏跟踪信号εd。理想的情况下I=－εd。

上述的基本HDR算法存在一个问题，当运载体有微小的转动速率时，算法将认为是εd，这将给计算带来误差。针对这个问题一些学者提出了一些改进的方法，在实际的应用中也起到了一定的效果。

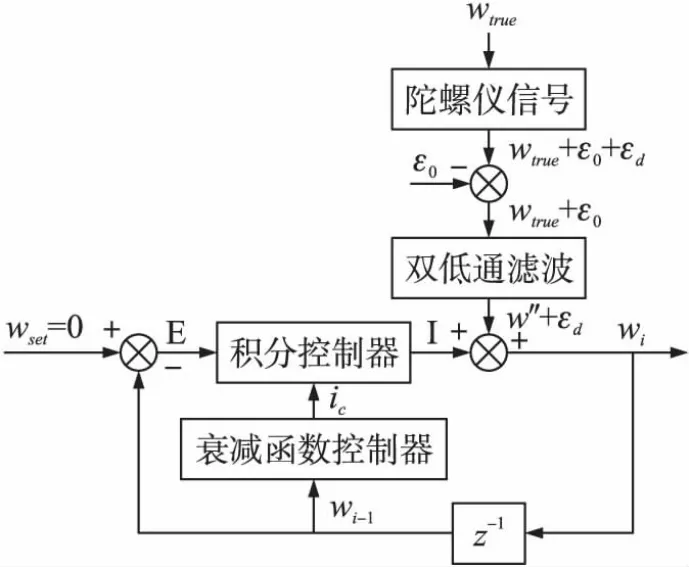
图4 HDR算法框图

本文基于HDR算法，对阈值线性函数［11］做了修改使得收敛速度明显加快，而且能较好的识别微小的角度输入，极大的减小了理论上存在的误差，有效的提高了算法的准确性。式(3)为改进后的阈值函数。图5为改进后的阈值曲线。

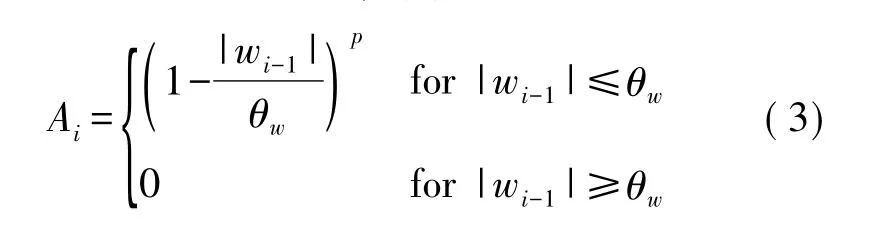
式(3)中Ai为要计算的衰减函数，θw为设定的阈值，p为设定的衰减因子(p≥1)。在阈值计算中增加衰减因子也正是本文对原HDR算法的改进。当p=1时就是原来的HDR算法，p的值应该根据具体的MEMS传感器的特性进行设定，因为不同型号的传感器其误差特性是不同的，特定的p值能使HDR算法对特定的传感器起到最好的补偿效果。

I为补偿因子，Sign为取符号函数，ic为固定的增量。

式中w″为经过双通滤波器滤波后的信号，wi就是经过HDR算法对零位随机漂移误差进行补偿后的输出信号。

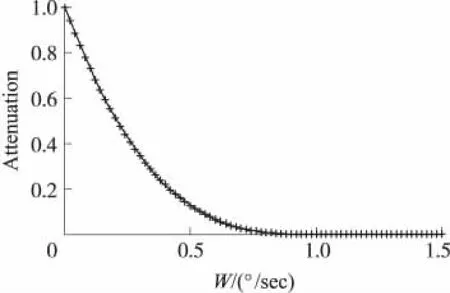
图5 阈值衰减曲线

在改进后的算法中，p值的选择很关键，当p值选择的越大收敛速度就越快，但HDR的作用范围将减小，在实际应用中，只要选择适当的p和θw值，总能使得输出结果更接近于真实的输入，得到理想的角速度输出。

4 试验验证与分析

为了对算法的精度做验证，本文采用Allan方差分析法对误差补偿后的数据做了评定，图6为经过误差补偿后陀螺仪数据的Allan方差分析图，表3为计算所得的噪声系数。

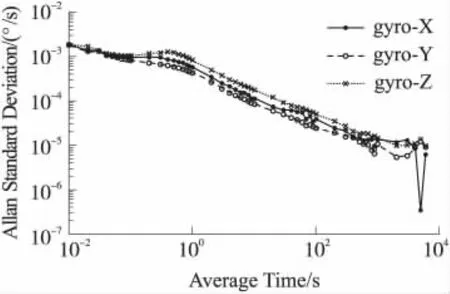
图6 误差补偿后的Allan方差分析图

表3 误差补偿后MEMS陀螺仪噪声系数

将表3和表2对比可以看出，经过误差补偿后陀螺仪的噪声系数降低了两个数量级。

除此之外，本文还以Voyager-IIA轮式机器人为平台进行了测试。测试时，将Nokia-Sensor-Box(内置有三轴陀螺仪)固定在机器人上，先让陀螺仪工作一段时间使其达到稳定状态，然后让机器人沿着一个边长为5 m的正方形轨迹运动两周，并回到初始状态。以100 Hz的采样频率测得陀螺仪数据。图7为采集到的陀螺仪Z轴原始数据和经过HDR算法处理后的数据，图中有8个矩形波，这分别是机器人在运动轨迹的拐角处输入的八个90°的转角。

本文分别用原始数据、经原HDR算法处理后的数据和经本文改进后的HDR算法处理的数据进行航向角的计算。理论上如果没有误差的存在，那么计算所得的相对初始位置的航向角度应该为零，若不为零，所得结果即为航向误差。3种数据的计算结果如表4所示。

表4 误差比较

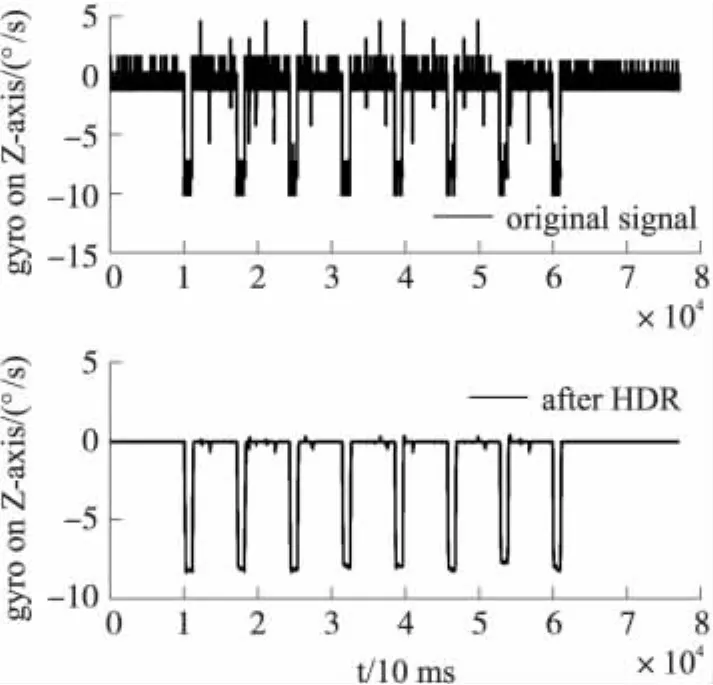
图7 Z轴陀螺仪数据

从表4中可以看出经本文改进后的HDR算法能更为准确的对零位误差进行补偿，使得补偿后的结果更接近于真实的输入。

5 结论

本文针对陀螺仪的零值偏移误差的不稳定性，提出了一种动态补偿的方法，改进了HDR算法，使得该算法对随机漂移误差的补偿更为准确。采用Allan方差分析法对补偿前后的数据作了对比分析，分析结果证明本文提出的补偿算法可以降低陀螺仪噪声系数两个数量级。以Voyager-IIA机器人为平台对两种算法做了验证，结果证明本文提出和改进的算法能更为精确的补偿零位误差。在试验中，本文改进的HDR算法中p和θw值都是通过实验的方法得出，目前还没能找到一种合理的算法计算出最优值，还有待下一步的研究。

［1］潘金燕，朱长纯，樊建民，等.微机械陀螺仪零位误差的研究［J］.西安交通大学学报，2006，40(4):480－483.

［2］施芹，裘安萍，苏岩等.硅微陀螺仪的误差分析［J］.传感技术学报，2006，19(4):2182－2185.

［3］邹学锋，卢新艳.基于Allan方差的MEMS陀螺仪性能评价方法［J］.MEMS 器件与技术，2010，47(8):490－494.

［4］赵思浩，卢明泉，冯振明，等.MEMS惯性器件误差系数的Allan方差分析方法［J］.中国科学:物理学 力学 天文学，2010，40:672－675.

［5］薛亮，李天志，李晓莹，等.基于MEMS传感器的微型姿态确定系统研究［J］.传感技术学报，2008，21(3):457－460.

［6］Hou H，El-Sheimy N.Inertial Sensors Errors Modeling using Allan Variance［C］//Proceedings of ION GPS/GNSS 2003.Portland:The US Institute of Navigation，ION，2003.2860－2867.

［7］IEEE Standard Specification Format Guided and Test Procedure for Single-Axis Interferometric Fiber Optic Gyros［S］.IEEE STD 647－2006.

［8］蒙涛，王昊，李辉.MEMS陀螺仪误差建模与滤波方法［J］.系统工程与电子技术，2009，31(8):1944－1948.

［9］李杰，张文栋，刘俊.基于时间序列分析的Kalman滤波方法在MEMS陀螺仪随机漂移误差补偿中的应用研究［J］.传感技术学报，2006，19(5):2216－2219.

［10］钱华明，夏全喜，阙兴涛.基于Kalman滤波的MEMS陀螺仪滤波算法［J］.哈尔滨工程大学学报，2010，3(9):1217－1221.

［11］Borenstein J，ojeda L，Kwanmuang S.Heuristic Reduction of Gyro Drift forPersonnelTracking System［J］.The Journalof Navigation，2009，62(1):41－58.

［12］钱华明，夏全喜，安笛，等.启发式算法在MEMS陀螺仪数据处理中的应用［J］.传感器与微系统，2010，29(3):109－111.

［13］杨叔子，吴雅，轩建平，等.时间序列分析的工程应用(上、下册)［M］.武汉:华中理工大学出版社，2007.