基于空间角度传递的多跳AOA三维定位算法研究与在地形建模上的应用*

夏 明，毛科技，何文秀，赵小敏，方硕瑾，陈庆章

(浙江工业大学计算机科学与技术学院，杭州 310023)

无线传感器网络(Wireless Sensor Network，WSN)技术是随着经济和社会发展而诞生的产物，是本世纪最具有影响力和改变人类未来生活方式的高技术领域四大支柱产业之一［1］。网络中大部分节点的位置是未知的［2］，而节点的随机分布和感知信息对位置的依赖，使得节点自身的准确定位是一个极其重要的条件。随着物联网的发展，把地形建模的能力加入传感器节点中，以辅助构建部署环境的地形模型，将对WSN的应用价值起到至关重要的作用。不管是军事应用环境，还是易发生自然灾害或遭受自然灾害破坏且人员无法到达的环境，如果能够利用节点位置信息进行地形建模，将有效地帮助相关工作的顺利开展。因此，研究三维定位并将此应用于地形建模上是有必要的、有价值的。

1 研究背景

现阶段，科研工作人员已经提出了一些三维定位 算 法，如 DCP3D［3］、Landscape-3D［4］、APIT-3D［5］、基于 SVM 的三维定位［6］、DFP 声源定位［7］等。常见的定位方法主要分为基于距离的定位和距离无关的定位两种。一般情况下［8］，基于距离的定位技术在定位精确度上要优于距离无关的定位技术，虽然需在节点上额外配备硬件设备，增加了成本和能耗，但定位精度一般要高很多。而在基于距离的定位技术中，采用测角技术得到的数据要比测距技术更准确，稳定性更好。因此，本文将在基于AOA(Angle Of Arrival，信号到达角度)定位的基础上进行研究。

DV-Hop定位算法［9］是由D Niculescu和B Nath等人提出的一个基于距离无关的多跳定位算法。DV-Hop三维定位算法是DV-Hop在三维场景中的自然运用，只需用三维坐标代替二维坐标即可。该算法思想比较简单，且容易实现，但是它采用区域的质心作为节点的位置坐标，必将导致定位精度不理想，且随着跳数的增大，造成的误差将变大。

Hady S.Abdel Salam和Stephan Olariu利用基于可升降式天线的信标节点和RSSI测距技术提出了一种具有地形建模能力的三维定位算法［10］。它的关键在于每个信标节点都配备了一个带有可移动的全向天线，必要的时候，天线可以上升或者下降几米的距离。该算法的优点是利用信标节点升降式天线的特性，巧妙地计算了节点的高度和二维坐标，算法整体复杂度相对较低。但存在的缺点是对信标节点的要求较高，需要具备升降功能的天线，提高了成本，且在某些特定的应用中并不适用，如在室内三维传感器网络、水下传感器网络中等。因此，该算法的适用范围比较小。

1.1 三维定位问题

针对不同的应用问题，国内外学者提出了各种二维定位算法，如D Niculescu和B Nath的APS自组网定位算法［11］，Srdjan Capkum 等人的 SPA算法［12］等。然而传感器节点往往被部署在三维空间中，因此确定其空间位置的过程就是无线传感器网络节点的三维定位。目前针对三维空间节点定位的研究还比较少，但对它的需求却日益迫切，是发展物联网亟待研究的重要课题之一，也是WSN领域的核心问题之一［13］。较二维定位而言，三维空间节点定位必然有一定的区别，主要包括以下几点:

(1)定位所需的信标节点增加。通常情况下，一个未知节点的二维定位需要三个信标节点，而三维定位则需要四个或者以上的信标节点才能实现。

(2)地形障碍对传输信号产生的影响。在三维空间中，地形障碍将带来非视距传输对信号造成的影响。

(3)不能满足特殊应用的需求。针对特殊应用场合的节点三维定位，如易发生地震的区域、易发生雪崩的雪山、地质活动较活跃的火山口等，定位结果必须能够准确反映出节点所处的位置，以帮助工作人员更好地了解这些危险地带正在发生的状况。

2 基于空间角度传递的多跳AOA三维定位算法的设计

假设网络中所有节点都存在一个表示自身正方向的主轴，通常为节点上两个接收机连线的中垂线。利用主轴可估计邻居节点相对于自身的方位角，即邻居节点发送数据的方向。这样就可以使用两个信标节点和它们分别与待定位节点形成的方位角即可获得待定位节点的平面位置信息。同理，如果假设信标节点不仅具有测定在x-y平面上信号到达角度的能力，同时还拥有测定信号到达俯仰角度的能力，则可通过这一新增加的变量实现在三维空间中对未知节点的定位。本文称该方法为简单AOA三维定位算法，并在此基础上，根据提高节点定位覆盖率的要求，提出了基于空间角度传递的多跳AOA三维定位算法MSAT3D AOA(Multi-hop Three Dimensional AOA With Space-based Angle Transmission)。

2.1 角度传递的原理

基于AOA的多跳定位思想最早是由D Niculescu和B Nath为解决Ad-Hoc网络路由算法需要对节点进行定位所提出的［15］，其核心技术是使待定位节点通过其它相邻节点角度传递的方式，获得在其直接通讯范围之外信标节点方位角信息的能力。如图1所示，L是信标节点，A，B，C均为相邻的未知节点且均有测量信号到达角度的能力。假设节点B和C均已测得其与节点L间的方位信息，同时也互相测得对方的方位信息及节点A分别与B，C之间的方位信息，则ΔABC和ΔLBC的所有内角便均可计算并确定，四边形ABCL的形状及其对角线与各边所形成的夹角也能确定，则节点A最终可通过这些角度信息并利用正弦定理等数学方法获得节点L与其主轴所形成的夹角，即确定了节点A和在其直接通信范围外的节点L之间的方位角信息。

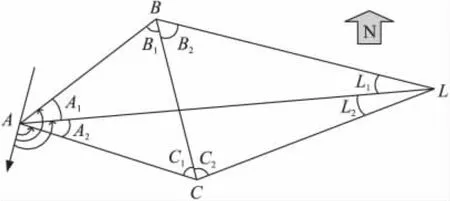
图1 角度传递示意图

2.1.1 三维空间中的角度传递定义

由于本文涉及的定位是在三维立体空间中进行的，因此，节点间角度传递也需要在同样的条件下进行。角度传递分为x-y平面上所形成的平面角和相对与x-y平面所形成的俯仰角两部分。其中，平面角取值范围为0°～360°，以x轴正方向为基准方向；俯仰角则为－90°～90°，以与x-y平面平行为基准方向。

如图2，A，B，C为具备三维空间中信号到达角度测量能力、自身位置未知且两两相邻(可直接通信)的未知节点，L为只装备了全向天线(不具备信号到达角测量能力)的信标节点，其中A为待定位节点。

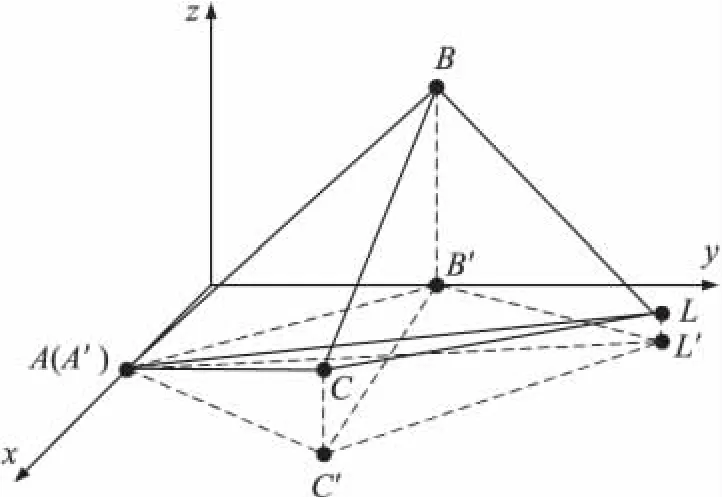
图2 三维空间图

2.1.2 三维空间中X-Y平面上的角度传递

图2 中，A'，B'，C'，L'分别为A，B，C，L在x-y平面上的投影位置，其投影所形成的各点关系如图3所示。在图3中，可以由节点上的测角设备直接测出角度大小的角为∠B1，∠B2，∠C1，∠C2和∠B'A'C'。另外我们还定义∠A'为∠B'A'C'，∠B'为∠A'B'L'，∠C'为∠A'C'L'。

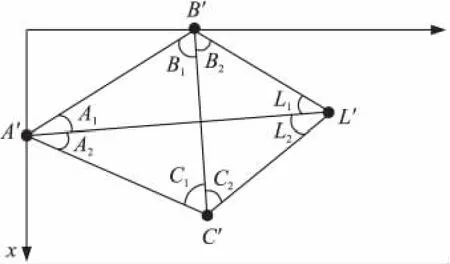
图3 节点在x-y平面上的投影

求解式(1)即可得到∠A1和∠A2。通过∠A1或∠A2与A'B'或A'C'的方位角信息相加减即可得到A'L'与绝对参考方向所成的方位角，即节点A得到了与其直接通信范围之外的节点L的方位角信息。由于在空间中这4个节点的位置关系不同，因此其在x-y平面上投影的位置关系除图3所示情况外还有5种，这里不再介绍。各节点处于不同位置关系时，各个角度之间的关系也会发生变化，而这也决定了如何通过测量和计算出来的角度来推出未知节点A与其直接通信范围之外的信标节点L的方位角信息。

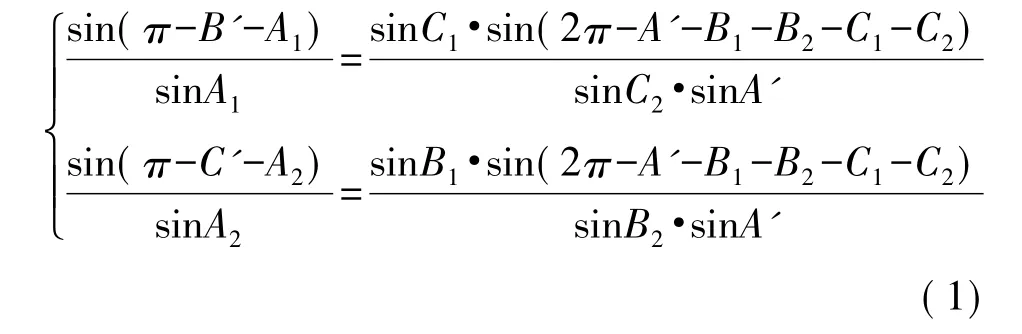
2.1.3 三维空间中俯仰角度的传递

图4为图2中节点在由ALL'三点所组成的平面上的投影，由空间解析几何知识可以证明，该平面垂直于x-y平面。在图4中，我们定义B'和C'分别为节点B和节点C在ALL'平面上的投影点。

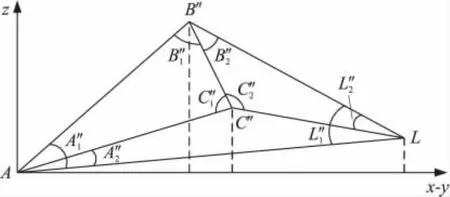
图4 节点在ALL'所在平面上的投影

节点感知信号三维到达角度的能力来自其所能测量的相对与x-y平面的俯仰角，但单独使用两个信号到达方位的俯仰角是无法判断这两个角在ALL'平面上的投影所形成的夹角的，所以本文在此处采用§2.1.2中所述x-y平面上对应投影角度关系，对投影在ALL'平面上的俯仰角进行分类。下面以节点A，B和C之间的位置关系为例说明如何采用此种方法对俯仰角度进行分类并计算在ALL'平面上的投影俯仰角间形成的夹角。

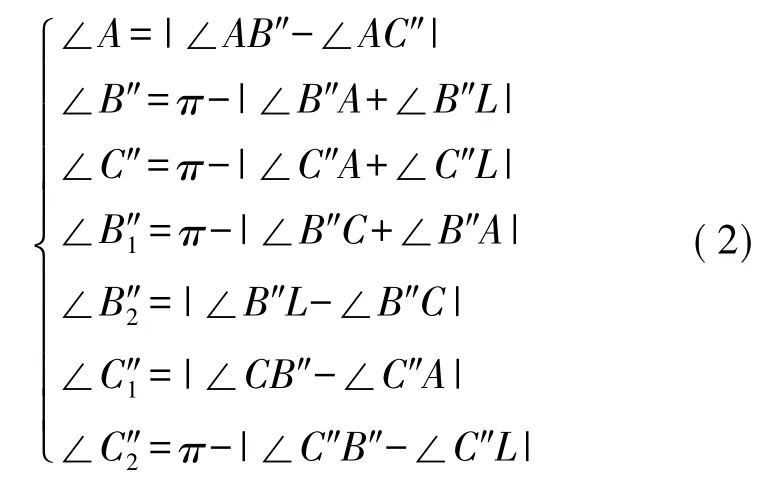
完成以上工作后，则可开始计算图4中各已知角和各节点测得俯仰角的关系如式(2)所示。至此，节点A便能通过上述方法，利用节点B和C与自身和节点L的角度关系，获得节点L关于自身的三维方位角。需特别指出的是，节点A，B，C，L在平面ALL'上的投影理论上也存在和x-y平面的投影一样，有6种角度位置关系，由于平面ALL'上的A，L点并非投影点，而是节点本身的位置，因此线段AL的长度即为两个节点间的实际距离，又由于投影在ALL'平面上的其它线段，其投影前本身的真实距离必定大于其投影线段的距离，因此在ALL'平面上凡是有可能出现有比AL长的其它线段的情况即为不可能出现之情况。

2.2 算法描述

MSAT3D AOA的核心思想是根据两个信标节点与待定位节点之间形成的两个方位角，及方位角与信标节点分别构成的两条直线方程来确定待定位节点坐标的，并在此基础上，融合了角度传递思想，通过获取无线射频范围外的信标节点相对于自身的方位角，实现了待定位节点利用通信范围外的信标节点进行定位的方法。

MSAT3D AOA分为参数配置和实际操作两部分。定位运行过程中需要使用的一些相关参数，必须预先写入所有节点，包括:(1)跳数阈值HopMax，指待定位节点通过角度传递获取若干跳数外信标节点信息时所能使用的最大值，可视网络规模、节点密度等情况而定；(2)手动设置或GPS获取信标节点坐标；(3)初始化未知节点，通过自身电子罗盘确定主轴方向与绝对参考方向(如正北方向)所成的角度关系，便于在全局坐标系中对节点位置进行计算，本文假设该坐标的x轴所指方向为正北方向，z轴正方向指向地心的相反方向。

根据MSAT3D AOA的操作顺序，可将定位过程归纳为以下5个步骤:

步骤1，初始化网络中的节点信息。所有节点都向邻居节点广播发送信息包，通过节点间信息的交换，建立“邻居信标节点信息表”和“邻居节点信息表”。

步骤2，满足条件的未知节点定位。若未知节点“邻居信标节点信息表”内记录数大于等于2，则用简单AOA三维定位算法进行定位，并将结果报给网络中的信标节点或汇聚节点，然后执行步骤3，若记录数小于2则直接执行步骤3。

步骤3，跳数阈值HopMax的判断。首先将存储在节点上的HopMax减1，若HopMax小于等于0，则停止，并将未知节点转入休眠状态，否则执行步骤4。

步骤4，未知节点间信标节点信息的互换。对于“邻居信标节点信息表”中记录数小于2的未知节点而言，已知条件无法满足自身的定位需求，必须通过向网络中邻居节点请求更多有用的信息。发出“信标节点信息”请求数据包的未知节点接收到各邻居节点发送过来的信息后，将这些信息存入“邻居节点的邻居信标节点信息表”中。

步骤5，分析“邻居节点的邻居信标节点信息表”。未知节点依次检查表中出现的信标节点，若某一信标节点记录数小于2，则放弃，并检查，否则，执行步骤6。如果所有信标节点均已处理，则返回步骤2。

步骤6，获取直接通信范围外的信标节点信息。对“邻居节点的邻居信标节点信息表”中所有具有同一个信标节点记录中的邻居节点排列组合，并选择其中两条记录，发送至数据分组中指定的两个邻居节点，邻居节点接收到该数据分组后，首先检查分组中另一个邻居节点是否存在于自身的“邻居节点信息表”中，若不存在，则返回“数据无效”信号给该数据分组的未知节点。然后未知节点执行排列组合中的下一个组合。如果所有组合都产生“数据无效”信号，则返回步骤5。若存在，则返回“数据有效”信号。然后未知节点对未知节点、两个邻居节点和它们共同的邻居信标节点使用角度传递，确定该信标节点对应于未知节点的方位角和俯仰角，并将该信标节点标识号、三维坐标及角度信息存入“邻居信标节点信息表”。

3 仿真实验与分析

本文在MATLAB下仿真实验，并与DV-Hop三维定位算法进行比较。假设在一个100 m×100 m×100 m的三维区域内随机部署100个节点。为使实验结果更加精确，本文采用统计的方法，对相同网络参数设置的实验仿真50次并取平均。对同一网络参数设置的不同算法的实验，均采用节点部署情况相同的数据进行比较。主要的性能指标有:(1)定位误差率，指可定位节点估算坐标与真实坐标的距离误差平均值；(2)定位覆盖率，指可定位节点在所有未知节点中的百分比；(3)不良节点比例，指不良节点占所有可定位节点的百分比，其定位误差大于节点通信的节点。

3.1.1 算法本身性能的实验结果与分析

本实验分别测试在不同跳数阈值和通信半径下MSAT3D AOA的各种性能。节点通信半径(Range)设定为35m，信标节点比例在5% ～30%间变化，分别测量跳数阈值为3和5的情况和通信半径为30、35和40且跳数阈值为3的情况下未知节点定位误差率、定位覆盖率、不良节点比例的变化情况。

图5(a)中定位误差率均随信标节点比例增加而大幅下降，这是由于未知节点获得直接信标节点比例和小跳数范围内信标节点比例随信标节点比例大大增加，而跳数阈值变化过大会导致更多误差被引入，造成定位精度下降，所以未知节点获得直接信标节点比例和小跳数范围内信标节点比例的增加能够显著提高定位精度，进而减少定位误差率。整体上看，所有节点的平均定位误差增加了，但是幅度在可控范围内，不会导致算法整体性能的大幅下降。图5(d)中定位误差率并没有随节点通信半径的减小而大幅增加。Range为30时，在信标节点比例较低时都只比30和35的情况高5%左右，而当信标节点比例增加后，其差别也越来越小。由此得出通信半径在部署区域和节点总数一定的情况下与节点密度成正比，通信半径越小，相当于节点密度下降，此时多跳定位占总定位比例不断提高。因此，在节点密度下降时定位误差率不会有显著的上升。

定位覆盖率上，如图5(b)，受信标节点比例和跳数阈值的影响并不大，均能使之维持在较高的水平。图5(e)中，定位覆盖率随通信半径的增加得到了显著的提高，即使在Range为30时，也能达到60%以上，由此得到算法在低节点密度(即低通信半径的条件下)依然拥有非常好的定位覆盖率，且通信半径的小幅度提高即能大幅度的提高定位覆盖率。同时可以看到，在Range达到35以上后有非常好的定位覆盖率指标，且信标节点比例可以维持在一个较小水平上。

图5(c)和图5(f)中，不良节点比例均维持在一个较低水平。由于产生不良节点的原因很多，而在仿真环境下主要是因为随机噪声的加入使得算法在处理一些边界情况时发生了难以预料的状况而导致的，而此类节点的定位误差一般都会远远大于算法整体的平均定位误差，由此可以得出正常定位的节点的误差相对整体的平均误差要更小，定位的精度要更好。同时，随着通信半径的减小，不良节点率并未发生显著上升，因此，也证明了算法在小通信半径条件下依然具有良好的定位精度。

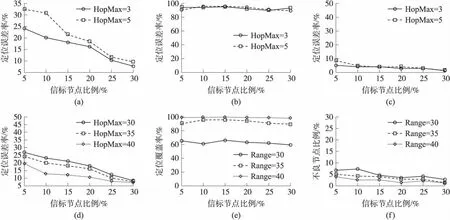
图5 MSAT3D AOA算法仿真实验结果图

在定位误差率上，如图6(a)，本文提出的测距有关的MSAT3D AOA远好于距离无关的DV-HOP。另外，MSAT3D AOA在信标节点比例为5%时的定位误差率要领先DV-HOP中比例为30%时的定位误差率达10个百分点以上。因此，从定位误差或定位精确度的角度上说，MSAT3D AOA比DV-HOP表现得更好。

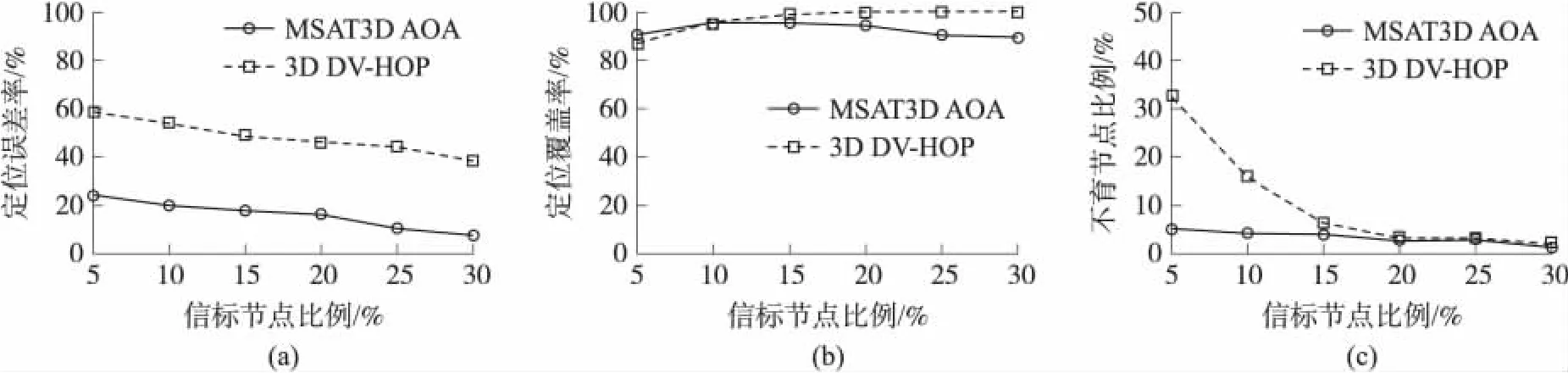
图6 仿真结果对比图

在定位覆盖率上，如图6(b)，MSAT3D AOA虽然略低于DV-HOP，但是基本都处于90%以上，已经达到了非常优秀的水平。此外，通过比较信标节点比例在10%以下的情况可以看到，MSAT3D AOA的定位覆盖率要稍优于DV-HOP，即在信标节点比例非常低的情况下也能达到较好的定位覆盖率。

在不良节点比例上，如图6(c)，与DV-HOP相比，MSAT3D AOA在信标节点比例较低的情况下表现的非常优异，且不会随信标节点比例的减少而显著增加。由此可知，DV-HOP在信标节点比例较少时具有非常高的不良节点比例是因为在多跳定位过程中多次估计所造成的误差积累非常大，导致最终的定位结果偏离真实位置的量也随之增大。而MSAT3D AOA产生不良节点的原因虽然也有多跳定位产生误差积累的因素存在，但其主要原因还是噪声的加入使得算法在处理一些边界情况时发生了难以预料的状况而导致的，而这种情况出现的概率非常低。因此，MSAT3D AOA在信标节点比例低的情况下也能有非常低的不良节点比例。

4 算法在地形建模中的应用

4.1 基于Delaunay三角剖分的地形建模

本文使用Delaunay三角剖分构建三角网实现基于WSN的部署环境地形建模。Delaunay三角剖分算法包括逐点插入法、分治法和三角网生长法3类。在数据量不是特别大时，一般使用最简单的、占用内存少的逐点插入法建立Delaunay三角网。逐点插入法［16］的基本步骤:(1)假设一个初始凸多边形，使其能包含点集中的所有点，如传感器节点；(2)在该凸多边形中构建Delaunay三角网，重复步骤3和步骤4，一次增加一个点，直到遍历整个点集；(3)计算包含新插入点N的外接圆对应的三角形，称为影响三角形；(4)将影响三角形的公共边删除，并把点N与所有影响三角形的顶点相连，实现点N的插入并保证生成的是Delaunay三角形。

4.2 算法应用于地形建模的结果分析与比较

定位完成后，利用节点x-y坐标值形成在三维空间中x-y平面上的点，使用Delaunay逐点插入法构建连续的三角形网，并以此为基础对所处环境地形建模。当在三角形的每一个顶点加入节点的z坐标值后，三角形网中每一个三角形便代表了空间中的一个面片，而这些面片所组成的图形即为该无线传感器网络部署环境的地形模型。图7是一个WSN部署环境的地形模型。假设在一个100 m×100 m×100 m立方体空间内部署500个节点，其中信标节点比例5% ～30%，通信范围为40 m，使用式(3)表示自然的地形形状数学模型。

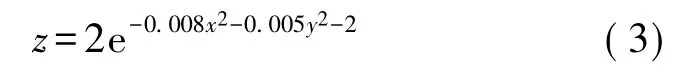
为模拟图7，本文在MATLAB下实验。首先部署未知节点和信标节点，并使用MSAT3D AOA定位。然后，使用Delaunay三角剖分构建三角形网，如图8所示。对于地形建模误差TME(Terrain Modeling Error)，可以用式(4)表示，其中，zi是节点i的实际高度，z'i为节点i的估计高度。

图9为MSAT3D AOA与基于RSSI三维定位算法在上述地形环境与条件下的地形建模误差。可以看到，在信标节点较少的情况下MSAT3D AOA的建模误差要略大于RSSI三维定位算法，但是需特别指出的是，在信标节点比例较小的情况下，本文所提算法依然能够保证对大多数节点的定位，这一点在仿真结果中已能证明，而RSSI三维定位算法是一种基于单跳的定位算法，在信标节点比例小的情况下覆盖率可以想见是肯定不会非常理想的。当信标节点比例不断提高后，本文所提算法在地形建模误差上迅速下降，这得益于随着信标节点比例的增加，使得算法中多跳定位所占比例减少，定位精度提高，而对于RSSI三维定位算法，由于信标节点的增加只是增加了未知节点能够获取信息的信标节点数，从而减少了由噪声产生的距离误差，这一变化无论从数量还是比例上来说都不会非常大，因此，其精度的提高也是有限的。

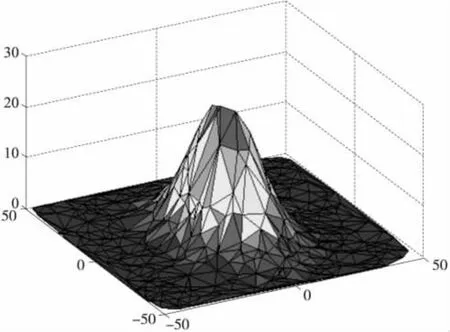
图7 部署环境地形模型

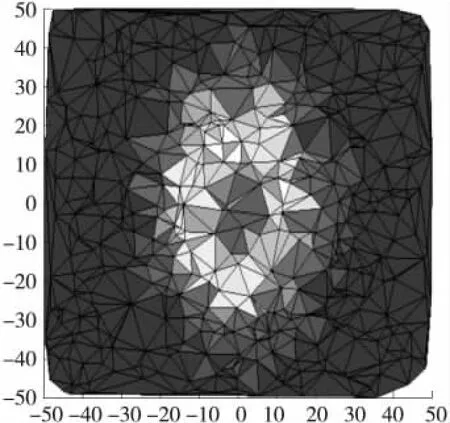
图8 传感器节点Delaunay三角剖分

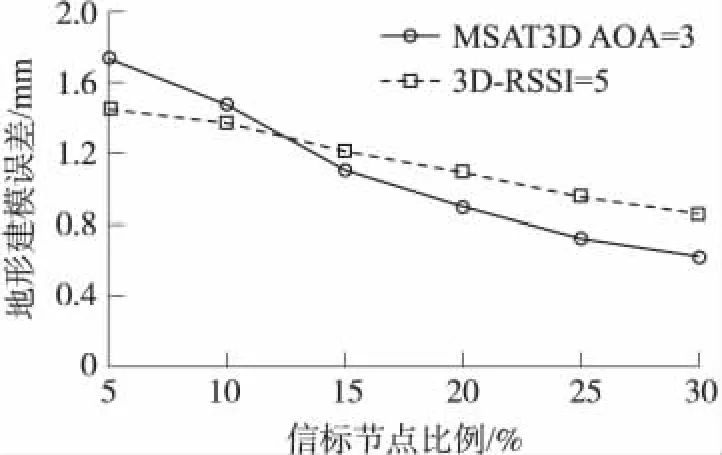
图9 地形建模误差比较

5 总结

本文从三维定位存在的问题入手，分析了三维定位技术的研究现状，考虑在室外环境的运用场景下，在简单AOA三维定位的基础上，结合三维空间角度传递的思想，提出了基于空间角度传递的多跳AOA三维定位算法MSAT3D AOA，使得邻居信标节点少于两个的待定位节点可以利用两个邻居节点的共同邻居信标节点，以获得距离一跳范围之外的信标节点的位置信息，再结合简单AOA三维定位就能够较好地减少不可定位节点的数量，提高算法的定位覆盖率。然后将MSAT3D AOA运用于地形建模中，使节点具有地形建模的能力，以辅助构建部署环境的地形模型，并将该算法运用到地形建模上，进一步验证了算法的可行性。

［1］Chong C Y，Kumar S.Sensor Networks:Evolution，Opportunities，and Challenges［A］.Proc of the IEEE，2003，91(8):1247－1256.

［2］Guoqiang Mao，Baris Fidan，Brian D O Anderson.Wireless Sensor Network Localization Techniques［J］.Computer Networks，2007，51，2529－2553.

［3］毛科技，赵小敏，邵奔，等.无线传感网络中基于共面度的三维定位算法研究与设计［J］.传感技术学报，2011，24(10):1481－1488.

［4］Liqiang Zhang，Xiaobo Zhou，Qiang Cheng.Landscape-3D:A Robust Localization Scheme for Sensor Networks over Complex 3D Terrains［C］//Proc of 2006 IEEE Conf on Local Computer Networks，2006:239－246.

［5］刘玉恒，蒲菊华，赫阳，等.无线传感器网络三维自身定位方法［J］.北京航空航天大学学报，2008，34(6):647－651.

［6］Ruohong Huan，Qingzhang Chen，Keji Mao，et al.A Three-Dimension Localization Algorithm for Wireless Sensor Network Nodes Based on SVM［C］//The 1st International Conf on Green Csircuits and Systems(ICGCS)，2010，651－654.

［7］刘立阳，张金成，吴中林，等.基于RSSI＆DFP的无线传感器网络声源目标定位算法［J］.传感技术学报，2011，24(10):1464－1468.

［8］Roy S，Chatterjee S，Bandyopadhyay S，et al.Neighborhood Tracking and Location Estimation of Nodes in Ad Hoc Networks Using Directional Antenna:A Testbed Implementation［C］//IEEE Proc of the Int Conf on Wireless Networks，Communications and Mobile Computing，2005，1－6.

［9］Niculescu D，Nath B.DV Based Positioning in Ad Hoc Networks［J］.Journal of Telecommunication Systems，2003，22(1/4):267－280.

［10］Hady S Abdel Salam，Stephan Olariu.A 3D-Localization and Terrain Modeling Technique for Wireless Sensor Networks［C］//Proc of 2nd ACM International Workshop on Foundations of Wireless Ad Hoc and Sensor Networking and Computing，2009，37－45.

［11］Niculescu D，Nath B.Ad Hoc Positioning System［J］.IEEE Globecom，2001，5:2926－2931.

［12］Capkun S，Hamdi M，Hubaux J P.GPS-Free Positioning in Mobile Ad-hoc Networks［A］.Proc of the 34th Annual Hawaii Int’l Conf on System Sciences［C］//USA:IEEE Computer Society，2001，3481－3490.

［13］王行甫，戴富泉，苗付友.基于TOA的三维无线传感器网络节点定位算法［J］.自动化与仪表，2008，12:1－9.

［14］孙利民，李建中，陈渝.无线传感器网络［M］.北京:清华大学出版社，2008:140－155.

［15］Niculescu D，Nath B.Ad Hoc Positioning System(APS)Using AOA［J］.Proc 22nd Annual Joint Conf of the IEEE Computer and Com-munication Societies(INFOCOM 2003)，2003，3:1734－1743.

［16］Anglada M V.An Improved Incremental Algorithm for Constructing Restricted Delaunay Triangulations［J］.Computer and Graphics，1997，21(2):215－223.