车辆悬架用电磁执行器的建模与试验研究*

来 飞

(重庆车辆检测研究院国家客车质量监督检验中心，重庆 401122)

悬架系统作为车辆底盘的重要组成之一，其性能的优劣对整车性能有重大影响［1］。主动悬架作为提升悬架系统性能的一种手段，兼顾了被动悬架系统难以解决的平顺性和操稳性之间的矛盾，是一种改善车辆悬架系统以及整车性能的有效途径。过去国内外研究者针对主动悬架系统的控制方法进行了大量的研究工作，但对于主动悬架系统中所采用的执行器的相关研究却相对较少。

相对液压悬架和空气悬架而言，电磁悬架系统具有较少的机械部件，系统配置更为简单灵活，同时密封性要求低，安全可靠性高。近年来随着电子器件性能的飞速发展，电磁主动悬架的优点越来越明显，它具有结构简单、响应快速以及可将振动能量进行回收等诸多优点，因此成为研究者们目前关注的热点［2－11］。Antonin Stribrsky等［2］利用Copley Controls公司的管型永磁直线电机TBX3810当做力发生器，Ismenio Martins等［3］将液压主动悬架和电磁主动悬架的优缺点进行了比较，指出电磁主动悬架性能要优于液压主动悬架，Bart L.J.Gysen 等［4］亦提出了一种电磁主动悬架系统来消除车身的俯仰和侧倾，仿真分析表明，与被动悬架系统相比，电磁主动悬架系统的车身侧倾角可减小94.4%，Seungho Lee等［5］同样利用管型永磁直线电机来充当主动悬架力发生器，Bose公司［6］经过多年研究成功研制出一种车辆电磁悬架系统，并已通过实车测试，但至目前为止，还没有关于这类电磁悬架系统的任何数据发表。

基于此，本文提出了一种圆筒型电磁执行器的结构设计，进而采用两种不同的建模手段对其进行了建模和仿真分析，其一为有限元建模，另一种为集总元件的动力学数学建模，两种方式所获得的电磁力响应结果基本一致，表明了模型的准确性。结合有限元模型，研究了执行器结构参数对电磁力的影响规律，进而选用合理的参数进行执行器样机的试制。通过对加工后的样机模型进行电磁力响应的试验测试，以及与有限元模型和集总元件动力学数学模型的相应比较，结果基本一致，进一步验证了模型的准确性。

1 电磁执行器的结构设计

本文所提出的电磁执行器原理与圆筒型直线异步感应电机的工作原理相似，都是利用对初级绕组通入三相对称交流电从而产生电磁力，其本质差别在于前者用于车辆悬架系统上时需要有较大的推力和行程，而后者通常用于往复直线运动的位置伺服控制。

自行设计的电磁执行器如图1所示，已申报国家发明专利(No.201010189918.7)。该电磁执行器采用星型联接，初级铁心采用0.5mm厚的硅钢片叠成。次级采用实心钢管，钢管外面覆盖一层2mm厚的铜层。此电磁直线执行器的有关技术参数如下:相数为3；执行器并联个数为3；初级槽宽为16 mm；初级齿距为20 mm；初级铁芯纵向长度为364 mm；次级有效长度为410 mm，气隙厚度为0.5 mm；动行程为100 mm；每相串联匝数为300；铜线直径为1.12 mm；同步速度为6 m/s；额定电压为220 V；初级槽数为18；初级槽高为16 mm；初级齿宽为4 mm；初级外径为140 mm；次级外径为40 mm；绕组型式为单层饼式绕组；槽满率为0.735；电源频率为50 Hz。

图1 电磁执行器的结构示意图

2 电磁执行器的建模研究

建立一个恰当的仿真模型是研究系统静态和动态特性以及控制技术的理论基础［14］。本文采用两种方式对执行器进行建模研究，分别为电磁有限元建模和Matlab/Simulink集总元件动力学数学建模。通过两种不同的建模手段一方面可用来验证执行器模型的准确性，此外有限元模型能较好地分析执行器结构参数对电磁力的影响规律，而集总元件数学模型仿真快速，能较好地用于执行器控制方面的研究。

2.1 电磁执行器的有限元建模及仿真分析

采用电磁有限元仿真软件Flux对执行器进行建模和仿真分析，其几何模型和有限元模型如图2所示。建模过程包括以下六个步骤:(1)几何建模；(2)网格剖分；(3)材料属性的设置；(4)电气特性的关联；(5)边界条件的施加和求解；(6)仿真结果分析。图2为执行器的有限元模型，共计节点数26508个，单元数12 709个。

图2 电磁执行器模型

在对执行器进行仿真求解之前，需施加相关的边界条件:1)初级速度和次级速度均为0 m/s，即将执行器两端固定不动；2)对执行器初级绕组施加相电压峰值为220 V，频率为50 Hz的三相对称正弦交流电。图3为磁力线分布和瞬态电磁力响应，可以看出，电磁力的瞬态峰值可达3 000 N左右，经0.15 s达到稳态，稳态力约为1 600 N。

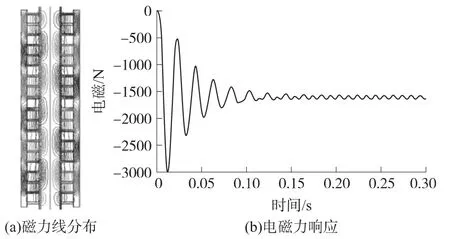
图3 有限元模型仿真结果

2.2 电磁执行器的集总元件动力学建模及仿真分析

在建立该执行器的集总模型前，为简化研究，作以下假设:①不考虑磁路的饱和情况，认为材料的磁场特性为线性的；②不考虑执行器齿槽力的影响。考虑执行器动态纵向边缘效应的T型等效电路如图4所示。其中Rrf(Q)和Lm(1－f(Q))均为考虑动态纵向边缘效应的影响而引入的修正项。

图4 电磁执行器的T型等效电路

基于以上分析和图4所示的T型等效电路，考虑动态纵向边缘效应的影响，在旋转感应电机数学模型的基础上，建立起电磁直线作动器同步旋转dq0坐标系统下的数学模型［12－13］。

电压方程为:

磁链方程为:

其中，通过电压方程可求出磁链:

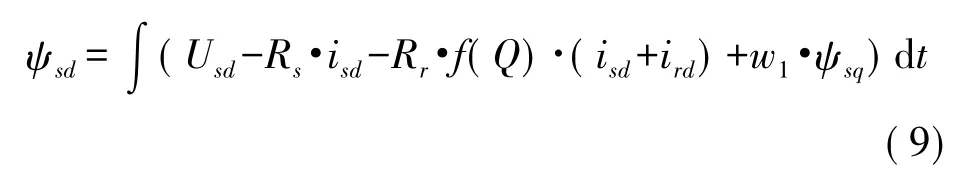
同理，可以求出其它3个磁链的表达式。然后可通过磁链方程求出电流:

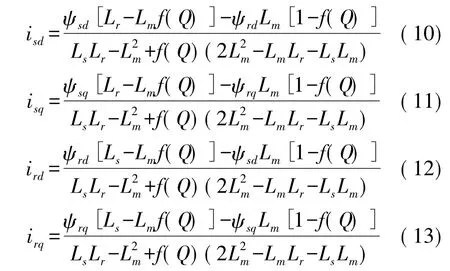
最终可获得执行器电磁力的表达式:

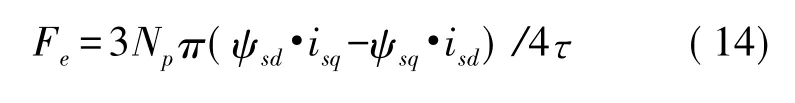
由牛顿第二定律，可得运动学方程:

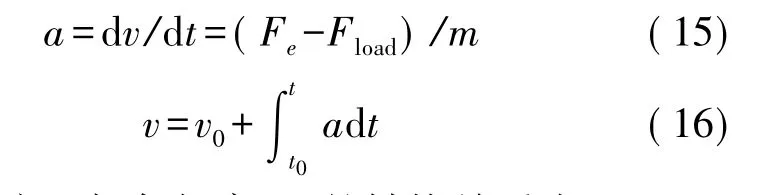
运动速度v与角频率wr的转换关系为:

其中:U为电压；i为电流；ψ为磁链；下标d，q为dq坐标系；下标s，r为初级、次级；Rs，Rr为初级、次级等效电阻；Ls，Lm，Lr为初级自感、互感、次级自感；Fe为电磁推力；Np为极对数；τ为极距；Fload为负载力；m为执行器负载质量；a为加速度；v0为运动初速度；v为运动速度；w1为初级磁场角频率；wr为次级磁场角频率；ws=w1－wr为转差角频率。

通过在Matlab/Simulink中建立起执行器的动力学模型如图5所示。执行器初级绕组相电阻为1.7 Ω，次级铜管电阻为1.3×10－5Ω，初级绕组相电感为5 mH。施加如下边界条件:①固定执行器的初级与次级；②对初级绕组通入三相对称正弦交流电，电源线电压有效值120 V，频率50 Hz。

图5 圆筒型电磁执行器仿真框图

图6为有限元模型与集总动力学模型的仿真结果对比，可以看出，有限元模型的峰值要比集总元件动力学模型的峰值大，其主要原因可能在于集总动力学模型没有考虑材料磁场的非线性所造成。总体看来，两种不同方式获得的电磁力响应基本一致。

图6 有限元模型与集总动力学模型的电磁力仿真对比

2.3 电磁执行器结构参数对电磁力的影响

2.3.1 气隙厚度对电磁力的影响

边界条件的施加与2.1节相同。图7为初级与次级气隙厚度发生变化时对电磁力的影响规律，保持初级内径不变，次级外径随气隙变化发生相应的改变。图8为不同材料的渗透深度与频率的关系。可以看出，随着气隙厚度的增加，电磁力的峰值和稳态值都有所下降。气隙厚度为0.5 mm时，电磁力最大，其峰值为－2 983 N，稳态值为－1 604 N；气隙厚度为2 mm时，电磁力最小，其峰值为－2 518 N，稳态值为－1 350 N。

图7 初级与次级气隙厚度对电磁力的影响

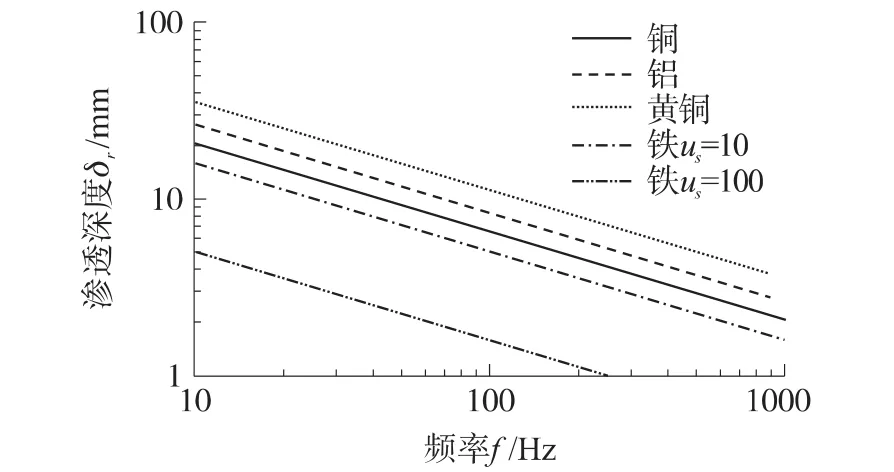
图8 不同材料的渗透深度与频率的关系

2.3.2 次级铜层厚度对电磁力的影响

图9为次级铜层厚度对电磁力的影响规律，可以看出，当铜层厚度由0.5 mm增加到1.5 mm的过程中，电磁力随铜层厚度的增加而增加；但当铜层厚度由1.5 mm增至4 mm的过程中，电磁力随着铜层厚度的增加呈下降的趋势。

图9 次级铜管厚度对电磁力的影响

实际上，当铜层厚度发生变化时，执行器内部存在着两种变化:一是随着次级导电层厚度的增加，等效气隙在增大，致使电磁力减小；二是随着次级铜层厚度的增加，铜层电阻减小，感应电流增加，致使电磁力增加。当铜层厚度由0.5 mm增至1.5 mm的过程中，原因二起主导作用，致使电磁力增加，而随着厚度的进一步增加，原因一起主导作用，结果导致电磁力随铜层厚度的增加而下降。综合考虑，铜层厚度取2 mm较为合适。

3 电磁执行器的实验研究

实验测试是研究执行器的另一重要手段，通过实验可验证仿真模型的准确性，还可进一步研究和掌握执行器的内在规律，提高理论研究和工程技术水平。为此加工了圆筒型的电磁直线执行器样机模型，其具体的结构参数见文中第1节。

3.1 执行器的稳态电磁力测试

对加工后的样机模型进行了稳态电磁力响应的测试，图10为在某厂进行实验的测试现场照片。通过三相自耦接触调压器GSGC2－6对电源电压进行调节，电源频率保持50 Hz不变，通过拉压力传感器获得执行器不同电压下的电磁力。

图10 执行器的稳态电磁力试验

在试验过程中，对次级完全充满和次级处于不同位置的两种情况进行了测试。由于受调压器功率的限制，最大所能调节的线电压有效值为120 V，对应于相电压的70 V。实验结果如图11所示。可以看出，随着电源电压的增加，执行器的电磁力会随之增加，电磁力的大小与电源电压的平方成正比关系；同时还可发现，执行器次级充满程度越大，电磁力越大，电磁力的大小与次级充满程度近似成正比例关系。

图11 次级不同位置下电磁力与电源相电压的关系

对前面所建立的执行器有限元模型施加与试验相同的激励，并对其进行仿真分析。图12为执行器次级完全充满下，电磁力与电源相电压的关系，可以看出，仿真结果与试验数据基本吻合。

图12 执行器次级完全充满下的试验与仿真对比

3.2 执行器的动态电磁力测试

对于车辆主动悬架执行器而言，除静态推力满足要求外，更值得关注的是其动态响应，因此还需对其动态电磁力响应进行测试。为此特搭建了如图13所示的简易试验平台。此时通过三相可控硅调压器ST35P－V－R－110－N－N 对电源电压进行调节，电源频率保持50 Hz不变，通过AutoBox DSPACE对可控硅的输入电压进行控制调节。

图13 执行器动态电磁力的试验测试平台

对执行器斜坡控制电压输入、方波标量控制电压输入、方波矢量控制电压输入及正弦控制电压输入四种情况下的电磁力响应进行了测试，试验结果分别如图14所示，同时将相同输入下的集总动力学模型仿真结果进行了相应的比较。可以看出，试验数据与仿真结果基本一致。

图14 不同控制电压输入下的电磁力仿真与试验对比

4 结论

(1)利用电磁感应定律的基本原理，设计制作了一种适合车辆主动悬架工作的大行程和大推力的新型电磁直线执行器，为主动悬架执行器的设计开发提供了一种新思路。

(2)从离散有限元和集总动力学两个不同的角度出发，以执行器的电磁力为切入点，建立了一种能够详细分析执行器结构参数影响的复杂有限元模型和一种抽象的用于执行器控制研究的集总元件动力学数学模型。

(3)对加工后的执行器样机模型进行了稳态和瞬态电磁力的试验测试，并与上述仿真模型进行了相应的对比分析，试验数据与仿真结果基本一致，表明了执行器仿真模型的准确性。

后续将在此基础上开展执行器驱动控制和主动悬架台架试验方面的研究工作。

［1］雷良育，周晓军.基于虚拟样机技术的汽车平顺性仿真分析［J］.传感技术学报，2006，19(6):2646－2649.

［2］Antonin Stribrsky，Katerina Hyniova，Jaroslav Honcu，et al.Energy Recuperation in Automotive Active Suspension Systems with Linear Electric Motor［C］//2007 Mediterranean Conference on Control and Automation，2007，July 27－29:1－5.

［3］Ismenio Martins，Jorge Esteves，Gil D Marques，et al.Permanent-Magnets Linear Actuators Applicability in Automobile Active Suspensions［J］.IEEE Transactions on Vehicular Technology，2006，55(1):86－94.

［4］Bart L J Gysen，Johannes J H Paulides，Jeroen L G Janssen，et al.Active Electromagnetic Suspension System for Improved Vehicle Dynamics［C］//IEEE Vehicle Power and Propulsion Conference，September 3－5，2008:1－6.

［5］Seungho Lee，Won-jong Kim.Active Suspension Control with Direct-Drive Tubular Linear Brushless Permanent-Magnet Motor［C］//American Control Conference，Hyatt Regency Riverfront，St.Louis，Mo，USA，2009:5498－5503.

［6］Jones W D.Easy Ride:Bose Corp.Uses Speaker Technology to Give Cars Adaptive Suspension［J］.Spectrum IEEE，2005，42(5):12－14.

［7］Bart L J Gysen，Johannes J H Paulides，Jeroen L G Janssen，et al.Active Electromagnetic Suspension System for Improved Vehicle Dynamics［C］//IEEE Vehicle Power and Propulsion Conference，September 3－5，2008:1－6.

［8］Seungho Lee，Won-jong Kim.Active Suspension Control with Direct-Drive Tubular Linear Brushless Permanent-Magnet Motor［C］//American Control Conference，Hyatt Regency Riverfront，St.Louis，Mo，USA，2009:5498－5503.

［9］Mirzaei S，Saghaiannejad S M，Tahani V，et al.Electromagnetic Shock Absorber［C］//Electric Machines and Drives Conference，IEEE International，2001:760－764.

［10］Babak Ebrahimi，Mir Behrad Khamesee，Farid Golnaraghi.A Novel Eddy Current Damper:Theory and Experiment［J］.J.Phys.D:Appl.Phys，2009，42:1－6.

［11］RYBA D.Semi-Active Damping with an Electromagnetic Force Generator［J］.Vehicle System Dynamics，1993，22:79－95.

［12］de Groot D J，Heuvelman C J.Tubular Linear Induction Motor for Use as a Servo Actuator［J］.IEE PROCEEDINGS，1990，137(4):273－280.

［13］叶云岳.直线电机技术手册［M］.北京:机械工业出版社，2003.

［14］雷美珍，戴文战，夏永明，等.双定子动磁铁式直线振荡执行器的力特性分析［J］.传感技术学报，2010，23(11):1570－1575.