基于近似模型的y轴微机械陀螺系统级优化*

吕湘连，何 洋

(西北工业大学陕西省微/纳米系统重点实验室，西安 710072)

优化一直是设计中的一个重要命题。在MEMS设计中也一样，可行高效的优化方法一直是设计者们追求的目标［1－6］。尤其在系统级设计中，好的优化方法对设计者快速得到满意设计方案，减少仿真迭代次数都具有非常重要的意义。

一般的优化问题都可以表达成一个通用形式:

优化目标:minf(xi)，(i=1，2，…，n)

约束条件:gk(xi)≤0(k=1，2，…，I)，hj(xi)≤0(j=1，2，…，J)

但是，相比于一般的优化问题，MEMS系统级优化存在很大的特殊之处。MEMS因为其多学科交叉、多域耦合的特点，要得到其优化目标的的函数形式，即得到f(xi)的具体表达形式，是非常困难的。文献［7］中，通过复杂的公式推导得到了微机械陀螺的优化目标函数——灵敏度与七个待优化参数之间的函数表达式，在此基础上基于遗传算法的全局搜索得到了一组理想的优化解。与上述方法类似，即在得到优化目标函数解析表达式的前提下进行优化设计的还有很多［8－11］。

然而，事实上，对于一个MEMS优化问题，优化目标函数表达式的获得往往不都是这么有经验可循，而且上述优化方法建立在得到解析的优化目标函数的基础之上，不是严格意义上的系统级优化。而且对于设计工具中的优化模块而言，需要提供给设计者的应该是一种相对容易操作和实现的优化方法。

为了体现MEMS系统级优化问题和一般优化问题的特殊性，首先需要对当前MEMS系统级模型进行简单介绍。

1 MEMS的系统级模型

统一建模方法是当前MEMS系统级建模一致使用的方法，该方法采用同一种建模方法和同一种语言，如硬件描述语言，对系统进行建模和描述，因此用一个仿真器即可实现对整个系统的仿真。西北工业大学提出的多端口组件网络模型(MuPEN)方法，就是基于统一建模方法的思想提出的一种具体系统级建模规范［12］。依此开发的MuPEN模型库，成为MEMS系统级建模的基础。

MuPEN方法把MEMS器件按照功能分为多个功能结构部件，并把其建模为参数化多端口组件。各功能结构部件的行为通过组件的端口变量信号表征。通过组件端口的相互联结形成的网络，表征整个MEMS器件。多端口组件的端口一般与功能结构部件自由度对应。组件的端口信号之间的关系采用低阶常微分代数方程描述，以加快系统的仿真计算速度。

但是，基于MuPEN方法的MEMS系统级仿真，其特征之一在于:系统级行为模拟不是基于显式表达的解析式完成的，而是通过组件端口的相互联结形成的网络，再根据其内部能量和信号流动来完成的，而这一行为往往通过某一仿真平台，如Saber来实现。这就造成了MEMS系统级优化问题和一般优化问题的不同之处在于:MEMS系统级优化问题的优化目标:minf(xi)，(i=1，2，…，n)，其函数表达式不能直接得到，而在优化问题中，优化目标的函数表达式往往是决定后续优化搜索的基础。因此，如何直接得到准确的优化目标函数表达式，成为实现MEMS系统级优化问题的关键，而本文就探索了一种近似模型的方法来克服这一问题。

2 基于近似模型的MEMS系统级优化方法

基于近似模型的MEMS系统级优化方法，是在给定MEMS器件结构及其待考察性能指标和优化变量的条件下，基于多端口组件库构建MEMS器件的系统级模型，在试验设计的基础上进行系统级仿真，通过对仿真试验结果进行回归分析建立待考察性能指标和优化变量之间的函数关系，即近似模型，基于近似模型写出优化目标和约束条件的数学表达式，对其进行优化并得到优化结果。

该方法最大的特点和效果就是，通过近似模型的获得，来解决现有MEMS系统级优化问题中优化目标函数不能直接得到的问题。

3 优化实例——y轴微机械陀螺

为了体现本文提出的系统级优化方法的可行性和有效性，作者给出了一个相对简单的优化实例。图1分别为一个微机械陀螺的三维结构示意图和设计参数示意图。待优化变量包括器件厚度t，梁宽w，梁长l1，l2，l3。各已有几何参数和材料参数为:质量块长700 μm，质量块宽600 μm，材料弹性系数E:130GPa，密度ρ:2 330 kg/m3，泊松比 λ:0.22。作为约束条件，各待优化参数取值范围为:3 μm≤w≤20 μm，3 μm≤t≤20 μm，50 μm≤l1≤1 000 μm，20 μm≤l2≤1 000 μm，20 μm≤l3≤1 500 μm，且要求l1－l3≥0。

图1 y轴陀螺结构示意图和设计参数示意图

对于该陀螺，我们最关注的性能参数是其驱动模态谐振频率fx和检测模态谐振频率fz尽可能接近从而达到模态匹配的效果，且希望其频率值在3 000 Hz附近。

在使用本文提出的基于近似模型的方法对y轴微机械陀螺建模时，首先在Saber Sketch中建立器件的多端口组件网络系统级模型如图2所示。

由于优化参数有5个，而且各参数的取值范围比较大，为了使得在有限次计算的情况下获得更好的采样数据，本文选用了均匀试验设计方法，对各参数(因素)选取15个水平，按照U15(155)的均匀试验设计表选取了15组试验方案。由于该y轴陀螺的关键性能指标分别是驱动模态的谐振频率fx和检测模态的谐振频率fz，这两个指标也就是该器件的待考察性能指标，因此，对每组试验方案，在Saber平台下进行系统级仿真，得到相应的fx和fz值，具体试验方案和相应的待考察性能指标结果如表1。

表1 y轴陀螺的均匀试验设计方案及相应的待考察性能指标结果

因为均匀设计表无整齐可比性，故在均匀试验设计中需用回归分析方法来处理试验数据，通过回归分析建立待考察性能指标和优化变量之间的函数关系。使用Matlab软件编程进行回归分析，分别得到驱动模态的谐振频率fx与检测模态的谐振频率fz与优化变量之间的二次回归方程，如下:

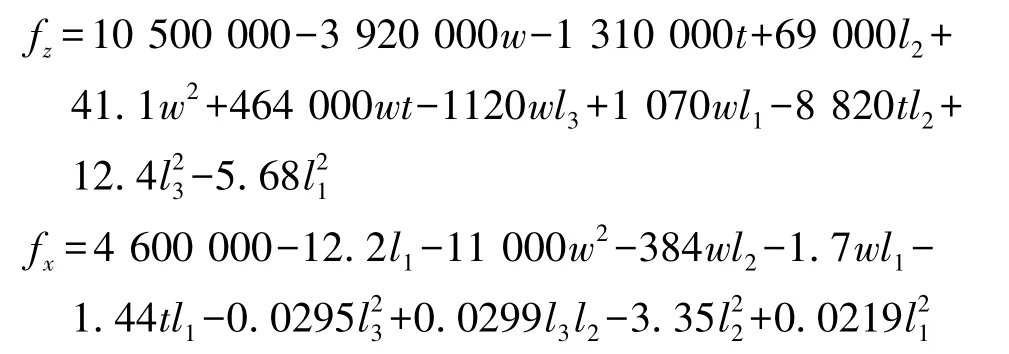
为了衡量该近似模型和采样点数据之间的误差，这里分别计算其误差向量的 2－范数R2为0.983 8和0.981 9，满足数据拟合中R2值最好大于0.9的要求，近似模型比较准确的反映了采样处待考察性能和待优化变量之间的函数关系。

在得到驱动模态的谐振频率fx与检测模态的谐振频率fz与优化变量之间表达式的基础上，写出显式的优化目标函数并不困难:

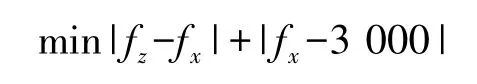
优化目标函数中，|fz－fx|表示驱动模态的谐振频率fx与检测模态的谐振频率fz的差值，|fx－3 000|表示驱动模态的谐振频率fx与目标值3 000Hz的差值，优化目标是使这两部分的和最小，也就是使fx与fz差值最小，同时fx在3 000 Hz左右。

结合优化目标和约束条件的数学表达式，采用序列二次规划算法实现优化。得到的优化结果如表2。

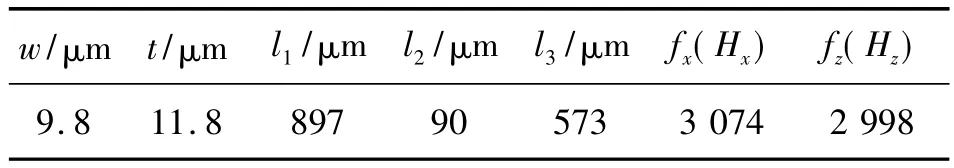
表2 y轴陀螺的优化结果

4 结果及总结

至此，基于近似模型进行y轴陀螺的系统级优化完成。在所得的优化参数下，经过多端口组件网络的方法进行系统级仿真，得到驱动模态的谐振频率fx和检测模态的谐振频率fz分别为3 074 Hz和2 998 Hz，两者之间相差76 Hz，较好的实现了模态匹配，且都在3 000 Hz的设计要求附近，约束条件也得到了满足。该优化方法为提高所设计器件的性能具有参考意义。

［1］John K Coultate，Colin H J Fox，Stewart McWilliam.Application of Optimal and Robust Design Methods to a MEMS Accelerometer［J］.Sensors and Actuators A，2008(142):88－96.

［2］Zhun Fan，Jiachuan Wang，Sofiane Achiche.Structured Synthesis of MEMS Using Evolutionary Approaches［J］.Applied Soft Computing，2008(8):579－589.

［3］Min Liu，Kurt Maute，Dan M Frangopol.Multi-Objective Design Optimization of Electrostatically Actuated Microbeam Resonators with and without Parameter Uncertainty［J］.Reliability Engineering and System Safety，2007(92):1333－1343.

［4］Raulli M，Maute K.Topology Optimization of Electrostatically Actuated Microsystems［J］.Struct Multidisc Optim，2005(30):342－359.

［5］李平，石云波，朱正强.MEMS高g加速度传感器固有频率的优化及验证［J］.传感技术学报，2010，23(3):388－392.

［6］方华军，刘理天.压电折叠梁微执行器的低电压优化设计［J］.传感技术学报，2008，21(3):465－468.

［7］Yuan Weizheng，Chang Honglong，Li Weijian.Application Application of an Optimization Methodology for Multidisciplinary System Design of Microgyroscopes［J］.Microsystem Technology，2006，12:315－323.

［8］Papila M，Haftka R T，Nishida T，et al.Piezoresistive Microphone Design Pareto Optimization:Tradeoff between Sensitivity and Noise Floor［J］.Journal of Microelectromechanical System，2006，15(6):1632－1643.

［9］Mukherjee T，Iyer S，Fedder G K.Optimization-Based Synthesis of Microresonators［J］.Sensors and Actuators A，1998，70(2):118－127.

［10］Apolstolyuk V A，Logeeswaran V J，Tay F E H.Efficient Design of Micromechanical Gyroscopes［J］.Journal of Micromechanics and Microengineer，2002，12:48－54.

［11］Han J S，Kwak B M.Robust Optimal Design of a Vibratory Microgyroscope Considering Fabrication Errors［J］.Journal of Micromechanics and Microengineer，2001，11:662－671.

［12］霍鹏飞，马炳和，苑伟政.基于组件网络方法的微加速度计建模与仿真［J］.航空学报，2003，24(5):466－470.