一种改进的Two-way中继协作系统下的节点选取和功率分配策略*

刘顺兰，徐光建

(杭州电子科技大学通信工程学院，杭州 310018)

协作通信技术通过用户间彼此共享天线，形成虚拟的MIMO信道从而获得空间分集，有效的对抗了无线通信中的多径衰落，提高了传输质量。文献［1－2］中最早提出了协作分集的概念以及基本的协作协议。协作通信除了应用在传统的蜂窝移动通信系统当中之外，在Ad-hoc网络和传感器网络当中也得到了广泛的应用，如文献［3］中就提出了一种用于无线传感器网络的节点协作算法。

到目前为止，有关中继协作通信技术的相关研究大都基于One-way系统，然而，One-way系统因为其半双工的工作模式造成了频谱效率的低下。因此Rankov B等人在文献［4］中分析并推导了AF和DF模式下Two-way中继系统的系统容量。但上述文献没有考虑到中继选择的问题，基于此，Yindi Jing在文献［5］中提出了一种在Two-way网络模型下存在多个放大前传中继节点的中继选择(RS，Relay selection)策略，并通过严格的误码率分析证明了该策略能够获得全分集。

提高Two-way系统性能的方法除了选择合理的中继节点进行中继转发之外，有效的无线资源分配方案也能够提升系统性能，主要包括跨层优化和功率分配。文献［6］中运用V-BLAST技术提出了一种用于协作式传感器网络的跨层优化方案。文献［7］是通过考虑中继节点处的最大似然信道估计来获得最佳分配因子，实现功率的优化分配。Petar Popovski等人在文献［8］中首次把物理层网络编码(PNC，Physical Network Coding)引入到 Two-way无线中继信道中，并提出了两种物理层网络编码方案，即三步方案和两步方案，其中三步方案采用的转发协议就是DF，而两步方案又包括AF，JDF(Joint Decode-and-Forward)和 NDF(Denoise-and-Forward)。但到目前为止，把PNC和中继选择以及功率分配三者结合起来的文献还不多见。

本文就是在文献［5］和［8］的基础上，首先介绍了一种Two-way DF中继系统下的双向中继选择(BRS，Bidirectional Relay Selection)策略，该策略就是通过同时考虑中继节点处的接收信噪比和中继节点到目的节点的信道增益两个因素来实现最终的中继选择。在选择并确定最佳中继节点后，然后基于物理层网络编码(PNC)，提出了一种Two-way中继协作系统的最优功率分配策略。

1 系统模型和协议

一个两终端多中继节点的Two-way系统模型如图1所示，其中T1和T2是用户终端节点，T3是候选中继节点，并假定有n个，且假设T1和T2之间不存在直传链路，每个节点都采用半双工的工作模式。hi和gi分别表示T1和T2到第i个中继节点的信道系数。

图1 两终端多中继的Two-way信道模型

终端T1和T2之间的信息交换是在两个阶段中完成的，每个阶段要求一个时隙。在第一阶段，称为多接入阶段(MAC，Multiple access)，终端T1和T2分别广播自身数据x1和x2到候选中继节点，然后依据本文将要介绍的双向中继选择(BRS)策略筛选出最佳中继节点；第二阶段，按照一定的规则［9］，筛选出的中继节点对接收到的信息进行解码映射，得到网络编码数据x3=x1⊕x2(⊕表示两个数据分组之间的网络编码运算，通常情况下是异或运算(XOR))，然后广播给两个终端，此阶段也称为广播阶段(BC，Broadcasting)。由此可以把基于最佳中继选择的多中继Two-way模型简化成如图2所示，图2中T3就是图1第二阶段中的，x1，x2分别是T1和T2的发送信号，x3是中继节点的发送信号。h和g分别表示T1→T3链路和T2→T3链路的信道系数。根据节点之间的对称性可以假设T3→T1链路和T3→T2链路的信道系数也分别为h和g。

图2 最佳中继确定后的Two-way信道传输模型

假设所有的信道都是平坦衰落信道，则第1时隙，T3接收到的信号为:

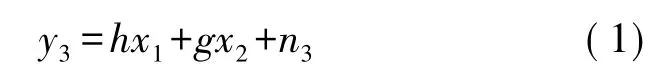
其中n3是均值为0，方差为1的加性高斯白噪声，且与两终端的信号x1，x2线性无关。

中继T3接收到信号后，按照一定的规则把接收数据y3转换成经物理层网络编码调制的信号x3，并转发至终端T1和T2。若中继节点处不采用译码并重新编码的转发形式，只是简单的通过物理层网络编码映射来产生PNC调制信号x3，则终端得到的信号可以写为:

式(2)、式(3)中，x3=x1⊕x2，n1，n2分别是终端T1，

T2处的服从均值为0，方差为1的加性高斯白噪声。根据文献［4］中对Two-way中继系统中可达速率和的分析，Rsum可以写作:

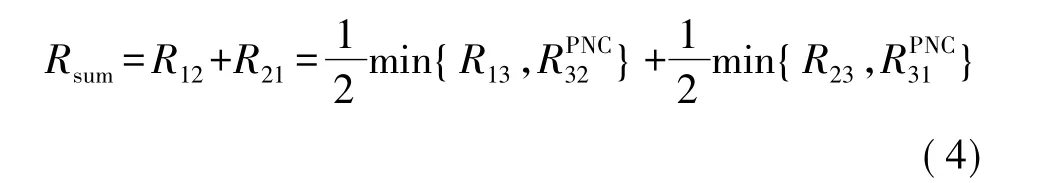
其中R12，R21分别表示从T1到T2和从T2到T1的可达速率，即信道容量。而Ri3和分别表示终端Ti，(i=1，2)和中继节点T3在第1和第2时隙中的链路容量。表示如下:

式(5)和式(6)中P1，P2分别表示终端T1和T2的发射功率，P3是经PNC调制后中继节点转发的功率，σ2是噪声方差，在本文中令σ2=1。

2 联合中继选择和功率分配策略

2.1 双向中继选择策略(BRS)

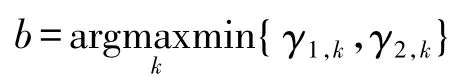
假设网络中存在n个中继节点，设置中继节点处的信噪比门限值是γth，当某个中继处的信噪比满足:

则该节点称为可靠候选中继节点，此时已假定噪声方差 σ2为 1。hi，(i=1，2，…n)表示终端T1到第i个中继的信道系数，也称为信道增益。假设可靠候选中继节点集合为φ，则有:

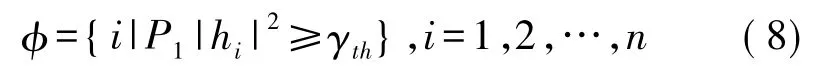
然后从候选中继节点集合φ中选择一个具有最佳信道增益的节点，作为中继到T2的传输信道，选择出的节点满足:

这样选择出来的中继不仅保证了链路间的传输质量，还有效的提高了系统性能，使得各链路状态达到最佳。

2.2 基于PNC的一种Two-way中继协作系统的最优功率分配策略

2.2.1 最优化问题的建立

根据上述BRS策略选择出最佳中继节点之后，系统中的功率分配问题就转换为在总功率Ptot受限的条件下，基于Two-way中继信道可达速率和最大化的准则，如何实现两个终端节点T1和T2以及选择出来的最佳中继节点T3三者之间的最优功率分配问题，简单表示为:

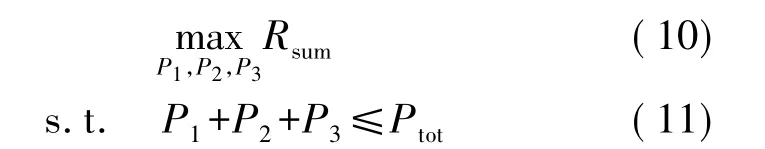
采用物理层网络编码(PNC)转发协议的一大特点就是中继不需要明确的对单个终端的信号进行译码，而是采用简单的星座映射产生PNC调制信号，然后发送到两个终端。由式(4)、式(5)、式(6)可知，中继处的发送功率P3同时影响R12和R21，进一步的还会影响功率P1和P2。因此为了简化最优功率分配问题，可以采用如图3所示的柱状图来表示各信道链路的容量，其中左边的表示第一组链路对，即T1→T3链路和T3→T2链路，两者中的最小值就是R12；右边的表示第二组链路对，即T2→T3链路和T3→T1链路，两者中的最小值就是R21。其中左边的“useless power”表示R13高出的那部分无用的功率。而右边的“excess power”表示高出R23的那部分过剩的功率。

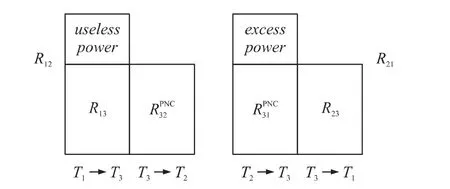
图3 等功率情况下Two-way中继信道的各链路容量

图3所展示的就是Two-way中继信道在P1=P2=P3的条件下各链路容量的大小，它还有个前提就是假设T1→T3链路状况比T2→T3链路状况好，即|h|≥|g|。但是考虑到Two-way系统的对称性，对于|h|≤|g|情况下的功率分配和上述情况一样。本文只考虑第一种情况。且由图3可知，由于链路状态的差异导致了和两者之间不相等，若记差异为 ΔRPNC，令 σ2=1，由式(6)可得:

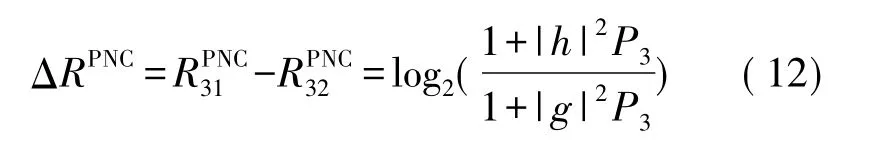
2.2.2 次最优功率分配策略

不难看出，等功率分配方案造成了功率的剩余，使得功率没有得到合理的利用，因此本文提出了一种最优功率分配策略，在分析最优功率分配策略之前，先对文献［11］中有关One-way中继信道模型的功率分配思想进行扩展，介绍一种次最优方案，即假设R13和R分别等于和，在总功率受限的情况

23下，结合式(5)、式(6)和式(11)可得到下列等式:

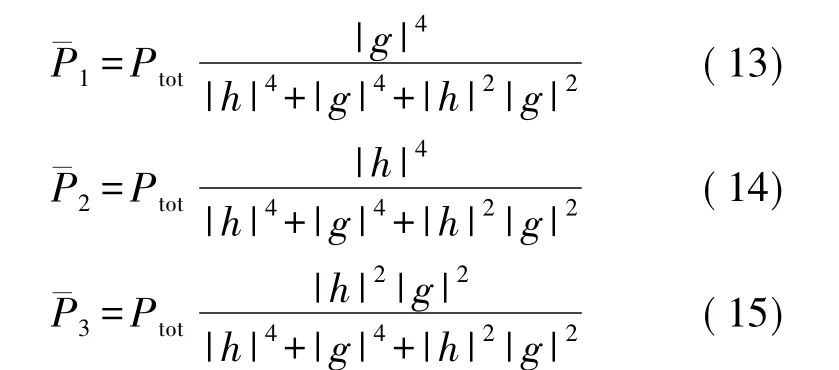
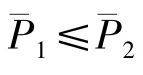
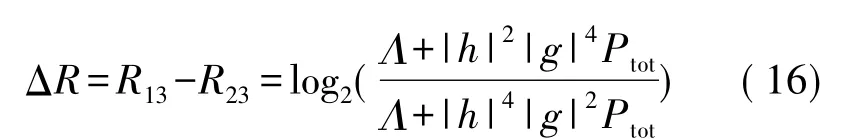
上式中 Λ=|h|4+|g|4+|h|2|g|2，由于|h|≥|g|，所以 ΔR≤0，即R13≤R23，因此R12≤R21。

2.2.3 最优功率分配策略

由式(16)不难看出，由于|h|和|g|不完全相等，导致ΔR≠0，而我们希望的是R12和R21的无比接近，即ΔR等于0.，因此可以通过进一步的调整次最优功率分配来实现最佳的功率分配策略，通过观察不难发现，可以将终端T2的部分功率ΔP2分配到终端T1和中继T3节点上，从而达到提高R12的目的，使其接近R21。设分配到节点T1和T3的功率分别为 ΔP1和 ΔP3，则有

设经过最优功率分配之后各节点的功率为:

为了不造成过剩的功率浪费，实现功率的最优

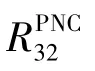
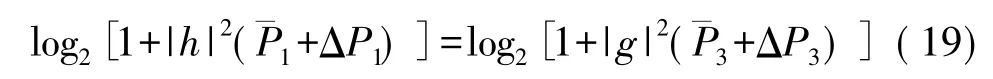
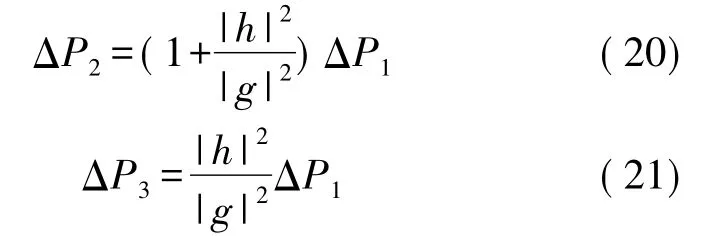
定义一个信道容量增益ΔRsum，则有:

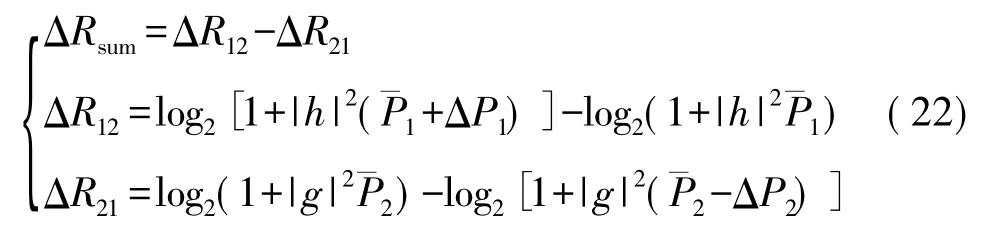
如果使得经过功率调整后的系统总的可达速率和得到提高，则必须满足ΔRsum≥0这个条件。结合式(22)化简后可得:

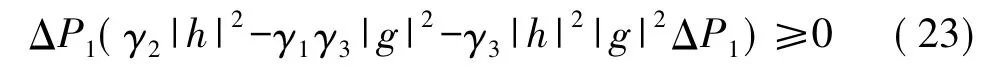
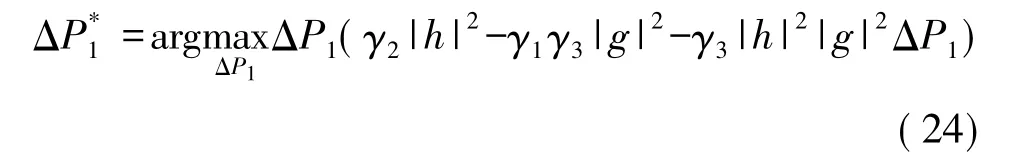
式(24)的最优化可以通过对ΔP1做一阶偏导并令它等于0，则:

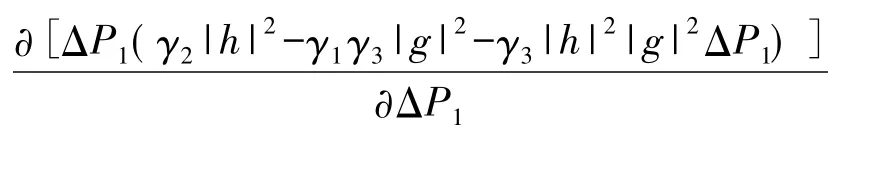
结合前面的式(20)、式(21)最终得出了使得ΔRsum最大的最优功率，即:

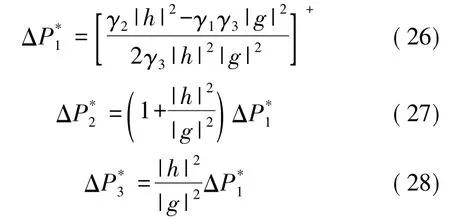
其中［x］+=max［0，x］，将式(26) ～ 式(28)的结果代入式(18)中就得到各节点最终所分配的功率，然后代入式(4)、式(5)、式(6)中求出系统的可达速率和。

上面讨论的是|h|≥|g|的情形，对于|h|≤|g|的情况可以采用相同的方法进行分析，这里不再赘述。

3 实验仿真及结果分析

本文对前面讨论的BRS中继选择算法以及基于PNC介绍的最优功率分配策略性能进行了仿真，并与其他几种算法做了对比分析。

仿真1:分析比较本文介绍的BRS中继算法和文献［12］中介绍的最大最小化(Max-Min，Maximum and Minimum)中继选择策略以及随机中继选择(RRS，Random Relay Selective)策略。

仿真参数:考虑一个一维的线性中继网络，如图2所示，记T1到T3的距离为d，不失一般性，将终端T1和T2之间的距离归一化为1。平坦衰落信道模型由下式给出:

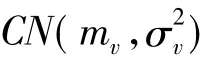
仿真结果:如图4所示，BRS算法较文献［12］介绍的最大最小化算法在性能上有明显的改善，尤其是在总功率较大的系统中表现的更突出。相对于RRS算法对系统总速率的提高幅度更大。如当总功率Ptot等于40 W的时候，BRS相对于RRS约有2.5 bit/(s·Hz)的提升，相对于 Max-Min也有近 1 bit/(s·Hz)的提升。

图4 各种中继选择算法的比较

仿真2:本文建议的基于PNC的Two-way中继系统中的最优功率分配方案和等功率分配方案以及One-way DF系统模型下的最优功率分配方案和等功率分配方案的比较。

仿真参数:信道模型和仿真1中所采用的信道模型一样，并假定中继节点T3就处在终端T1和T2的中点处，即d=0.5。

仿真结果:如图5所示，不难看出，Two-way系统无论是采用等功率分配还是采用最优功率分配方案较One-way系统在信道容量上都有很大的提高。例如，在信噪比SNR等于14 dB的时候，依次在等功率分配方案和最优功率分配方案两种情况下，Two-way中继协作系统的系统总速率都比One-way协作系统的系统总速率高出近3 bit/(s·Hz)。同时从图5中还可以看出，本文提出的基于PNC的最优功率分配方案较等功率分配方案平均取得了约1 dB的增益。

图5 基于PNC的最优功率分配算法和其他算法的比较

4 结论

本文主要考察了Two-way DF中继协作系统中联合中继选择和功率分配两个方面的问题。首先介绍了一种双向中继选择策略(BRS)，该策略不仅能够保证双向链路间的信道质量，同时还可以有效提高系统信道容量和频谱利用率，然后基于BRS策略和物理层网络编码PNC提出了一种最优功率分配方案OPA，该方案实现了系统速率和的最大化。仿真结果表明OPA方案较EPA方案平均取得了1 dB的增益，同时也验证了Two-way的系统总速率比Oneway的系统总速率约高出一倍。但是本文尚没有探讨的是基于Max-Min中继选择策略下的最优功率分配方案和本文建议的最优功率分配方案的性能比较，还有待下一步的研究。

［1］Sendonaris A，Erkip E，Aazhang B.User Cooperation Diversity-PartⅠ and Ⅱ［J］.IEEE Transcations on Communications，2003，51(11):1927－1948.

［2］Laneman J N，Tse D N C，Wornell G W.Cooperative Diversity in Wireless Networks:Efficient Protocals and Outage Behavior［J］.IEEE Transcations on Information Theory，2004，50(12):3062－3080.

［3］汪琼，张锋.无线传感器网络中的节点协作算法研究［J］.传感技术学报，2006，19(2):481－485.

［4］Rankov B，Wittneben A.Spectral Efficient Protocals for Halfduplex Fading Relay Channels［J］.2007，25(2):379－389.

［5］Jing Yin-di.A Relay Selection Scheme for Two-Way Amplify-and-Forward Relay Networks［C］//IEEE Wireless Communication ＆Signal Processing.Nanjing，China，2009.

［6］徐侃如，刘威，程文青，等.一种基于V-BLAST技术的多跳协作式传感器网络的跨层优化［J］.传感技术学报，2007，20(12):2688－2694.

［7］Jiang Bin，Gao Fei-fei，Gao Xi-qi，et al.Channel Estimation for Amplify-and-Forward Two-Way Relay Network with Power Allocation［C］//IEEE International Conference on Communica-tions，Dresden，Germany，2009:1－5.

［8］Popovski P，Yomo H.Physical Network Coding in Two-Way Wireless Relay Channels［C］//Proc.IEEE International Conference on Communication(ICC)，Glasgow，Scotland，2007:707－712.

［9］Zhang S，Liew S C，Lam P P.Physical Layer Network Coding［M］.Submitted to IEEE Trans.on Inform.Theory.

［10］唐伦，刘通，前斌，等.Two-way中继系统协作节点选择及功率分配策略［J］.电子与信息学报，2010，32(9):2077－2082.

［11］Zhang Q，Zhang J，Shao C，et al.Power Allocation for Regenerative Relay Channel with Rayleigth Fading［C］//Proc IEEE 59th Veh.Technology.Conference(VTC)，vol.2，pp，1167－1171，May 2004.

［12］Bletsas A，Khisti A，Reed D P.A Simple Cooperative Diversity Method Based on Network Path Selection［J］.IEEE Journal on Selected Areas in Communications，2006，24(3):659－672.