自相关过程的ARMA控制图
2012-10-21张志雷
张志雷
(河南财经政法大学统计学系,郑州 450002)
0 引言
为了解决过程自相关条件下的质量控制问题,人们提出了多种方法。由于自相关过程的统计控制状态可由时间序列的模型和参数来描述,因此,时间序列理论作为一种重要的方法被普遍用于解决自相关过程的控制问题。其中常见的一种思想是运用时序模型拟合的方法把自相关过程过滤成残差序列,由于残差序列独立同分布,因此可采用常规控制图进行控制,形成的控制图称为残差控制图[1](以下简称残差图),研究表明:残差图适用范围有一定局限性,当过程中、强度正相关且均值发生较大偏移时,残差图具有较好的使用价值[2]。另有学者则提出根据过程自相关结构,运用时序理论重新构造控制图的过程控制统计量,以达到提高控制图检测性能的目的。本文依据控制图设计基本思想,研究建立在自回归移动平均统计量基础上的ARMA控制图原理,并以链点检出概率和平均链长(ARL)为准则,系统分析了ARMA控制图的性能,并与残差图进行了较为系统的比较,结果有助于我们清楚认识生产中自相关过程的控制问题从而正确选用适宜的控制图。
1 ARMA控制图基本原理[3]
假设X1,X2,…是离散平稳序列,具有不变的均值和自相关结构,即E(Xt)=m(t∈Z),自协方差函数g(t)=cov(Xt,Xt+t)仅与滞后期t有关。根据时间序列理论中的ARMA模型,构造出ARMA控制图的统计量Zt可表示为:
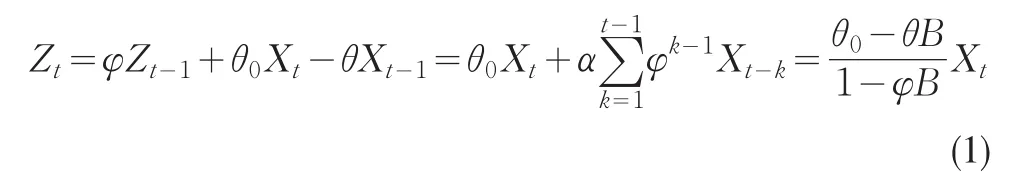
其中α=φθ0-θ,B为滞后算子。根据Zhang协方差计算方法【4】可证明式(1)中统计量Zt在自相关条件下也为平稳序列。易证E(Zt)=m,而序列{Zt}的自协方差函数是:

其中r(t)=g(t)/g(0)是序列{Xt}滞后t期的自相关系数。若t→∞且t=0时,上式则为控制统计量Zt的方差:

被检测过程的自相关形式可以用不同的时序模型来刻画,为具体说明ARMA控制图的基本原理,本文采用具有代表性的ARMA(1,1)模型表示被测过程,其形式为:

其中 ∣u∣<1,∣v∣<1,at~N(0,)。其方差和滞后一期的相关系数分别为:

那么,可用ARMA(1,1)模型关系式来简化稳定状态下Zt的方差,将以上两个公式带入到式(2)中并由r(k)=ur(k-1)(其中k≥2)可得:

因为Xt服从正态分布,所以Zt也服从正态分布,均值为μ,当t很大时,使用式(4)计算被测过程ARMA(1,1)的σz值。由统计量Zt,可建立ARMA控制图,其中心线为μ,上下控制限为μ±kσz。在用ARMA控制图进行控制时,由于受控过程Xt和检测过程Zt都为自相关过程,观测点在控制界限内呈现非随机排列的可能性大大增加,如连续七点单调上升或单调下降,因此仅用观测点是否在控制界限内作为判断准则,即当|Zt|>kσZ表明过程中存在异常原因。
2 ARMA控制图参数的选取
在稳健设计中,信噪比指标被用以度量产品质量特性稳健程度,表达式为R=μ/s。Zhang利用信噪比定义出的检测能力指数[5],用来衡量过程均值发生偏移时,控制图在各时点上检测出偏移的能力大小。基于同样思想我们可以根据信噪比这个指标来设定ARMA控制图的参数,通过信噪比比值的调整来增强控制图的检测效能。
假设t0时刻,由于异常原因使过程{Xt}的均值由零偏移到μ,则此时点及以后各时点控制统计量Zt均值的偏移形式可由式(1)得出:

进行迭代整理后,则在t0后均值的偏移形式可统一表示为:

由上式可知控制统计量均值的偏移程度取决于参数θ、f和过程{Xt}均值偏移程度m,而与被监控过程的参数u和v无关。当过程{Xt}均值在时刻T=t0偏移μ个单位后,控制统计量Z的均值变化形式服从(5)式,即在时点T瞬间偏移θ0m;随着时间t→∞,因为|φ|<1,其在新的均衡态下偏移ms=m,则时点T和均衡状态下的信噪比分别为:RT=μT/sZ和RS=μS/sZ。当过程{Xt}均值偏移程度统一用其标准差sx表示即m=δsx时,由(2)式可知,这两个信噪比可写成:

当过程均值发生偏移时,统计量Zt值位于控制限内的概率为:

其中U为标准正态随机变量,k通常取3。由式(10)可知,概率Pt与信噪比Rt大小有关。R值越大P值越小,则检出概率1-P值越大,单个链点对异常原因的检测能力也越大。则RT衡量ARMA控制图在过程{Xt}均值偏移时点T的检测能力;如果最初均值偏移未被检出,则均衡状态下的Rs对随后链点能否有效检测出偏移将起重要作用。因此,信噪比RT和Rs的取值决定了ARMA控制图的检测效能。
Jiang和Tsui总结了信噪比选取的一般原则【3】,若ARMA控制图的RT被调到很大,这时控制图能以较大概率在时点T迅速检测出偏移发生,如RT=4时,由式(10)可计算出控制图立即报警的概率约为0.8413;若RT小于3,则在异常发生初期控制图报警的概率将小于0.5,需要用随后的链点检测,此时Rs的取值将至关重要。然而Rs不能被调得很大,因为这将会导致RT很小,控制图及时发现异常原因的概率降低,延迟纠正错误的最佳时机。因此为了增强控制图对均值偏移的检出能力,必须选择适宜的控制图参数,使两个信噪比RT和Rs达到平衡。一般来讲,当Rs取值在3附近对于平衡RT和Rs是适宜的。当信噪比比值确定后,由于受控过程为平稳序列,其相关结构稳定,参数u,v不变,根据式(6)(7)相应统计量Zt的参数θ、f也就确定,具体取值则需要依据式(6)(7)和均值偏移程度计算得到的数表进行选取。在实际工作中,平稳序列的方差sx和相关系数r(k)均由样本数据估计,为了避免自相关结构估计误差对控制图准确度的影响,要求样本数据至少100个。
根据以上内容,我们总结出绘制ARMA控制图的步骤:
(1)确定待控制的质量指标并根据实际经验估计被测过程均值最有可能出现的偏移程度;
(2)由过程稳态下的样本数据估计自相关模型ARMA(p,q)的参数u和v以及滞后相关系数;
(3)对 f和b(|f|<1,|β|<1,β=θ/θ0),根据公式(6)(7)以及第一步确定的偏移程度计算出相应RT和Rs的数表;

(5)计算Zt的方差与均值,绘制出控制限,作出ARMA控制图;
(6)将测量数据在ARMA控制图中打点,判定过程是否稳态。
3 ARMA控制图检测性能的比较与分析
运用Matlab软件分别作10000次模拟运算,获得在不同均值偏移程度下,各控制图的ARL值,具体结果见表1。表中参数设置情况说明:第1列表示过程均值偏移程度为δ个sx单位;第2、3列是自相关过程{Xt}为ARMA(1,1)模型时的参数取值,其中at~N(0,1);第4、5列则为ARMA控制图相应统计量Z中参数f、θ取值,根据上节信噪比选取原则选取并由式(8)(9)计算得到。为了比较各控制图的检测能力,参数k取在过程稳态下使ARL大致为370的值。

表1 自相关模型为ARMA(1,1)时两种控制图ARL的比较
计算结果显示:除过程强相关且均值大偏移情况外,在绝大多数条件下,ARMA控制图的ARL要小于残差图,表明其对异常原因的检测能力较强,尤其在均值发生中小程度偏移情况更是如此。例如过程参数u=0.7,v=0.5条件下,ARMA控制图在均值偏移程度δ=0.5,1,2时的ARL分别为60.14、17.46、5.00,明显小于相应残差图的平均链长;而在δ=3时,ARMA控制图的ARL也略小于残差图,说明此时ARMA控制图对均值偏移的检出能力优于残差图。仅在过程强相关且均值较大偏移时,ARMA控制图的ARL要大于残差图,例如当u=0.9,v=0条件下,ARMA控制图在δ=2,3的ARL分别为18.78、4.75都大于相应条件下残差图,表明此时检测能力弱于残差图。因此,总体来讲,除序列强相关且均值较大偏移情况外,通过调整ARMA控制图中统计量Z的参数取值可以增控制图的检测效能。
4 ARMA控制图的蒙特卡洛模拟研究

图1 模拟数据的ARMA控制图

图2 模拟数据的残差控制图
为了更好地理解ARMA控制图的检测性能,我们使用蒙特卡洛模拟方法进一步从两个信噪比即各个链点检测能力角度,研究ARMA控制图算法对检测效果的影响。首先,利用Matlab软件随机生成基于ARMA(1,1)模型Xt-0.5Xt-1=at+0.5at-1,at~N(0,1)的360个数据,其中前150个是过程稳态下的随机数,后210个是过程均值偏移一个sx单位时的失控数据,由方差公式可计算出sx=1.5275。其次,由式(8)(9)计算出参数f和θ在取值范围内所对应的RT和Rs的数表,根据选取原则选出适宜的信噪比RT=0.501,Rs=3.01并确定相应的f=0.95、θ=0.117,最后根据式(2)计算出控制统计量Z的方差sz,作出ARMA控制图的控制限并对模拟序列进行控制。如图1所示,当均值在第151个点发生偏移后,ARMA控制图在第161个点显示超出控制限,发出第一个报警信号,表明过程存在异常原因。对相同模拟序列用残差图进行控制,如图2所示,图中最早报警点的序号为249大大滞后于ARMA控制图。通过模拟结果说明ARMA控制图的检测效果要明显优于残差图,用这种控制图方法对自相关过程进行控制是适宜的。
5 结论
建立在自回归移动平均统计量基础上ARMA控制图提供了一种灵活的策略来选择统计量参数,我们可以根据受控过程自相关结构选择控制统计量的参数,从而通过调整两个信噪比比值来提高ARMA控制图检测的灵敏度。研究结果表明除过程强相关且均值较大偏移情况外,在绝大多数条件下,ARMA控制图检测能力明显优于残差图。因此,对自相关生产过程进行控制时,可以考虑运用ARMA控制图来提高检测的有效性。
[1]Alwan,L.C.,Roberts,H.V.Time-series Modeling for Statistical Process Control[J].Journal of Business and Economics Statistics,1988,6(1).
[2]王斌会,张志雷.残差控制图检测能力分析及效率评价[J].统计与决策,2005,(4).
[3]Jiang Wei,Tsui K.L.A New SPC Monitoring Method:The ARMA Chart[J].Technometrics,2000,42(4).
[4]Zhang,N.F.A Statistical Control Chart for Ctationary Process Data[J].Technometrics,1998,40(1).
[5]Zhang,N.F.Detection Capability of Residual Control Chart for Station⁃ary Process Data[J].Journal of Applied Statistics,1997,24(2).
