总体中位数可信区间估计Bootstrap法样本含量的设置
2012-10-21陈国民
陈国民
(海军潜艇学院,山东 青岛 266071)
0 引言
Bootstrap法是以原始数据为基础的模拟抽样统计推断法,用于研究原始数据的某统计量的分布特征,广泛应用于可信区间估计、假设检验等问题。当用Bootstrap法进行统计分析时,需要从原样本(样本含量记为n)中随机有放回地抽取n*个观测单位,构成Bootstrap样本。关于Bootstrap样本含量n*的大小,一般认为,可以小于,等于或者大于原样本含量n[1]。但从有关Bootstrap法的文献来看,往往把Bootstrap样本含量n*设置为与原样本含量n相等[2]-[4]。本文拟运用计算机模拟方法考察Bootstrap样本含量n*对Bootstrap法总体中位数可信区间估计效果的影响,从而探讨Bootstrap样本含量n*的设置方法。
1 方法
用VFP编写程序进行统计模拟研究。
模拟步骤:
(1)模拟从标准正态分布总体X~N(0,1)中随机抽取一个样本,样本含量为n。
(2)从该样本中随机有放回抽取一个Bootstrap样本,Bootstrap样本含量为n*。
(3)计算获得的Bootstrap样本的中位数。
(4)重复步骤(2)~(3)B次(B=1000)。
(5)对求得的B个中位数按升序排序,找到2.5%(第25位)和97.5%(第975位)百分位数,即为由该样本估计的总体中位数的95%可信区间。
(6)判断求得的95%可信区间是否包含总体中位数0,如果包含0,则记正确1次;否则记错误1次。
(7)重复步骤(1)~(6)1000次,得到1000个可信区间。
(8)统计1000个Bootstrap可信区间包含总体中位数0的百分比,该百分比即为Bootstrap法总体中位数可信区间估计正确率的估计值。
参数设置:
模拟实验一:原样本含量n分别设置为5,10,50,100;Bootstrap样本含量n*分别设置为2,5,10,20,30,40,50,100,200。
模拟实验二:原样本含量n分别设置为2~50,100;Bootstrap样本含量n*分别设置为n,n-1,n-2,n-3,n-4。
判断标准:正确率越接近准确度100(1-α)%越好。本文α=0.05,所以,1000次模拟所得的正确率越接近95%越好。
2 结果与分析
模拟实验一结果见表1。从中可见:不论原样本含量n大小,Bootstrap法的正确率随着Bootstrap样本含量n*的增加而降低;当Bootstrap样本含量n*很小时,Bootstrap法的正确率远远大于95%,甚至可达100%;当Bootstrap样本含量n*很大时,Bootstrap法的正确率远远小于95%,甚至为0;当Bootstrap样本含量n*等于原样本含量n时,正确率接近或略小于95%。由此可以推断,当Bootstrap样本含量n*稍微小于原样本含量n时,正确率可能更接近理论准确度。
为了寻找最佳的Bootstrap样本含量n*,进行模拟实验二。结果见表2。从中可见:(1)当Bootstrap样本含量n*=原样本含量n时,若原样本含量n较小,则正确率偏低,随着原样本含量n增加,正确率逐渐提高并接近95%,当原样本含量n达到30时,正确率基本接近95%;(2)当Bootstrap样本含量n*=原样本含量n-1时,正确率仍然偏低,但当原样本含量n达到20时,正确率基本接近95%;(3)当Bootstrap样本含量n*=原样本含量n-2时,当原样本含量n达到10时,正确率基本接近95%;(4)当Bootstrap样本含量n*=原样本含量n-3时,正确率不再偏低,当原样本含量n达到5时,正确率基本接近95%;(5)当Bootstrap样本含量n*=原样本含量n-4时,正确率明显偏高,但当原样本含量n达到30时,正确率基本接近95%。
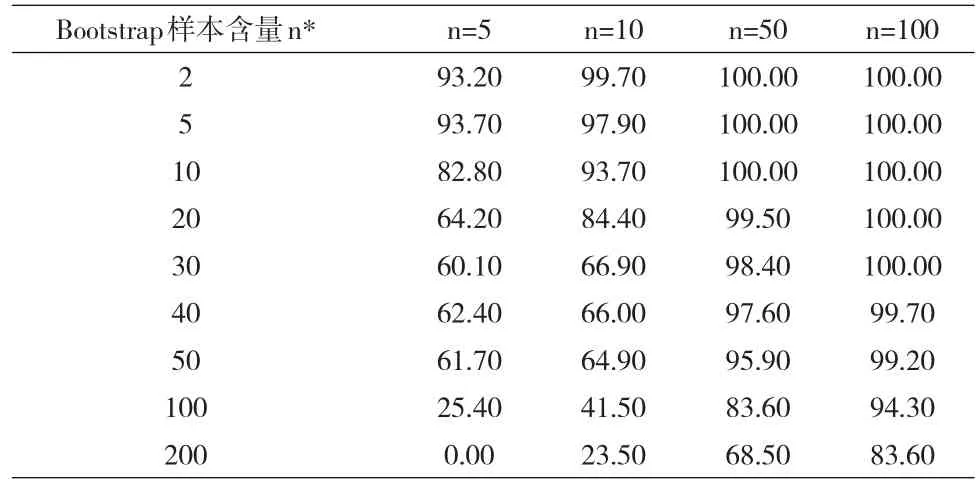
表1 Bootstrap样本含量n*对总体中位数可信区间估计正确率(%)的影响

表2 Bootstrap样本含量n*对总体中位数可信区间估计的正确率(%)的影响
为了定量考察Bootstrap样本含量n*对总体中位数可信区间估计准确度的影响,计算表2中各种设置时的误差(误差=正确率-95),不同设置时的误差比较见表3。由表3可见,当Bootstrap样本含量n*=n-3时,误差的标准差最小,说明误差的变异最小,同时,此时误差的均数也最小(P<0.05)。因此,结合前面的分析,可认为运用Bootstrap法进行总体中位数可信区间估计时,把Bootstrap样本含量n*设置为n-3时效果最好。

表3 各种设置时的误差比较
3 讨论
从有关Bootstrap法的文献来看,Bootstrap法的效果与Bootstrap样本含量n*无关,Bootstrap样本含量n*可以任意设置,既可以小于原样本含量n,又可以等于原样本含量n,还可以大于原样本含量n。但在实际应用中,往往把Bootstrap样本含量n*设置为与原样本含量n相等[1]-[3]。从本文的模拟结果来看,Bootstrap样本含量n*的设置对Bootstrap法准确度的影响很大,尤其是当原样本含量n较小时,Bootstrap样本含量n*更不能任意设置,否则,估计出来的可信区间误差很大。模拟结果表明,当用Bootstrap法进行总体中位数可信区间估计时,如果把Bootstrap样本含量n*设置得过小(远远小于原样本含量n),则得到的可信区间会很“宽”,从而导致可信区间的准确度远远高于设置的100(1-α)%;反之,如果把Bootstrap样本含量n*设置得过大(远远大于原样本含量n),则得到的可信区间会很“窄”,从而导致可信区间的准确度远远低于设置的100(1-α)%。
综合分析模拟结果,可得出如下结论:①如果原样本含量小于5,Bootstrap法的准确度过低,不宜用Bootstrap法估计总体中位数可信区间。②如果原样本含量不小于5,Bootstrap样本含量n*设置为原样本含量n-3最合适,可信区间的准确度非常接近理论准确度100(1-α)%。③如果原样本含量较大(大于30),Bootstrap样本含量n*可以设置为与原样本含量n相等,但不宜设置为大于原样本含量n。
需要说明的是,本研究只是对正态分布资料的总体中位数可信区间估计进行了模拟试验,而且仅设置了α=0.05这样一种情况,其结论未必适用于其它情况。对于偏态分布资料总体中位数可信区间估计,尚需进一步的研究。
[1]蔡雪亚,金丕焕,曹素华.用Bootstrap方法计算中位数的可信区间[J].中国卫生统计,2002,19(3).
[2]陈峰,陆守曾,杨珉.Bootstrap估计及其应用[J].中国卫生统计,1997,14(5).
[3]刘勤,金丕焕.Bootstrap方法及其在医学统计中的应用[J].中华预防医学杂志,1998,32(1).
[4]敖雁,王学枫,汤在祥,等.Bootstrap方法在平均数假设测验中的应用[J].中国卫生统计,2006,(6).
