走进数学王国探究数学奥秘

2012-10-20施培成

赤峰学院学报·自然科学版 2012年1期

关键词：公理化抽象性曲面

施培成

（郑州华信学院，河南郑州 451100）

走进数学王国探究数学奥秘

施培成

（郑州华信学院，河南郑州 451100）

本文试图从数学的内容、方法和意义，数学的理论结构和体系方法，分析数学的特征，探寻学好数学的关键所在，希望通过这些文字和历史小故事打开认识数学的大门.让学生了解数学的奥秘，消除对数学的误区，领略数学的趣味和魅力，增加学好数学的信心.

麦比乌斯曲面；哥尼斯堡七桥问题；欧拉公式；贝特朗奇论

1 数学是开启一切科学大门的钥匙

按照目前科学分类的方法，物质世界的运动按其矛盾的特性可分为自然科学，社会科学和思维科学三大基本领域，与这三大基本领域相对应，现代科学包括五大基本部类，即自然科学类、社会科学类、思维科学类、数学和哲学，它们的关系如下图1所示：

图1中黑体字表示大部类科学，圆括号表示次级类过渡学科或边缘学科.实线表示一级联系，虚线表示次级联系.

从图1中看到数学已经广泛地渗透到物质世界的各个领域，数学是现代科学中的基础学科，成为各门科学发展的共同工具，马克思说“一种科学只有成功地运用数学的时候才算达到真正完善的地步”.

数学蕴含了巨大的威力，它的领域日益扩大，它不仅为自然科学服务，而且在社会科学领域也离不开数学，谁要是不用数学为自己服务，总会有一天发现别人已经用数学来同自己竞争，21世纪人人都离不开数学.

2 数学的特征（Ⅰ）——高度的抽象性

充分认识数学的抽象性特征，并找出让自己能够适应并学会数学抽象的方法.

数学是人类历史上诞生最早的科学之一，数和形这两个基本概念是数学的两块基石.早在2000年前人们就认识数的重要性，古希腊数学家说：“庞大、万能和完美无缺是数字的力量所在，数是人类生活的开始和主宰者，也是一切事物的参与者”.缺少数字一切都变得混乱无序，数学的发展大体上也是围绕数和形这两个基本概念的提炼发展和演变而展开，例如大家熟悉的虚数i，起初只是在求解代数方程中出现，在很长一段时间里虚数i的价值和意义不为人们所理解，只把虚数之看作一个虚设的符号，直到18世纪70年代对i给予了几何解释建立了复变量x+yi于是应系统的研究，复变函数论诞生并把它应用在流体力学和地图制图学上，从此这种虚设的数i在数学上完全站住了.以及后来欧拉命名的公式e2πi的出现，e，π，i，1，2 这些“出身”完全不同的数，可用一个简明的公式表现出来，真是不可思议，让人对数学的发展产生惊讶、感奋，引来无穷遐想，这就是数学的奥妙和魅力.

数学的抽象与其他科学的抽象有明显的区别，数学的抽象是撇开对象具体内容，具体属性仅仅保留其中纯粹的数量关系或空间形式例如点、线、面、数、元素、集合、空间等等这些都是纯粹抽象的概念，这类基本概念无法用语言文字直接定义，它们各自的“意境”只能通过类比和联想加以思索.然而它们在数学研究和应用中发挥了不可取代的作用.人们的习惯常常是喜欢具体而不习惯抽象（看不见摸不着）甚至有一个“误区”认为学习高度抽象的数学，在实际中能有多大的用处？其实正好相反，因为抽象的数学概念和方法都是由大量的生活实践中整理概括抽象而来，一大批具有同一实际背景的事物通过类比联想和移植就可以再回到同一类型的实际问题中去，这就是说数学的高度抽象性和广泛应用性不但不矛盾而且相辅相成.在数学学习中要适应并且习惯它的抽象性，在求解应用题时，更要善于对实际问题运用抽象、联想和移植的方法、迅速地化难为易.请看下面两个小故事：

例1 在微积分下册讲曲面积分时提到麦比乌斯带，这是一个单侧曲面，它是由18世纪德国数学家麦比乌斯构造的，遗憾的是论文尚未发表作者就不幸故去，许多年后，被别人在他的遗作中发现，并把这个单侧曲面命名为麦比乌斯曲面而公开发表.更加有趣的是三百多年后在上海举世闻名的世界博览会的展览馆群中，有一个国家把这种麦比乌斯曲面设计使用在自己国家的世博会的展览大厅上，当参观的人群走在这种单侧曲面的参观通道上，感受到三百年前的古代数学文明与现代高科技的建筑文明融洽为一体成为世博会的一大亮点，这个抽象的麦比乌斯单侧曲面再次失而复得.我们敬佩那位建筑设计师他有厚重的数学底蕴，更有超常的把抽象应用到现实的能力，这个故事验证了一句民间谚语“是金子总是要发光的”.

例2 哥尼斯堡城位于普格雷尼河畔如图2a所示河中有大小两个岛，大岛南北两边各有两座桥与对岸相连，小岛南北两边各有一座桥与对岸相连，大小两岛之间又有一座桥相连，哥尼斯堡就是由南岸、北岸、大岛、小岛这四块陆地通过七座桥相连.旅游团希望能找出一条参观的路线使得从四块陆地的任一块出发每座桥只通过一次，不重复不遗漏在最后又回到原地，这就是历史上著名的七桥问题，这个问题困扰了当时众多的学者.许多年后由数学家欧拉解决了.欧拉先对问题作抽象简化，他用四个点A、B、C、D分别表示四块陆地，再用七条线段 AC，CA，CB，BC，AD，CD，BD，分别表示七座桥，七桥问题抽象为一条回路（图2b）的“一笔画”问题，欧拉进一步研究回路“一笔画”的充分必要条件，最后的结论是七桥问题无解.在这里我们又一次看到了用纯粹抽象的点线图形解决了复杂的应用问题.

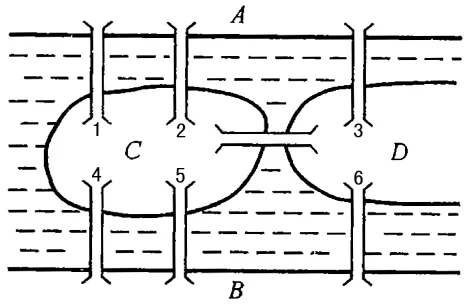
图2a

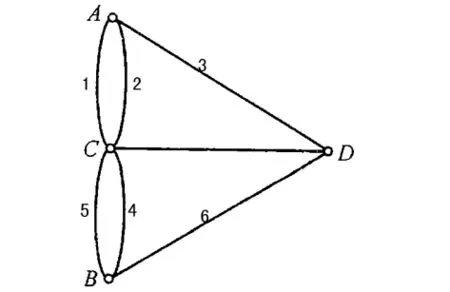
图2b

在近代的网络理论中“一笔画”问题更有重要作用.

数学的抽象性不仅表现在概念上，也表现在方法上，恩格斯说：“数学是一种研究思想事物的科学”.这是对数学抽象性的深刻概括.

3 数学的特征（Ⅱ）——数学理论具有严密的逻辑性，逻辑学是数学的生命

数学理论的建立无法通过实验验证和判断从古希腊开始形式逻辑就与数学紧密结合，数学命题的真伪只能借助于严密的形式逻辑原则来判断.

（1）数学思维的方法是开启思维的钥匙，有了科学的思维方法就能对许多原始资料进行合理的加工整理形成严密的理论体系，常用的数学思维方法有分析与综合，抽象与概括归纳与演绎等等.

（2）数学思维的形式是建构数学分支逻辑结构体系的“元件“，常用的是以下七种：

①概念：对原始的数学资料抽象整理去伪存真加工而成，它真实地反映事物的本质.

②定义：是揭示概念内涵的逻辑方法.

③判断：是反映事物具有或不具有某种属性（或关系）.

④命题：是用文字或符号表达判断的句子.

⑤演绎（又称推理）是由一般到特殊的推理方式它给出命题的前提与结论之间的必然联系，因为演绎推理是合乎逻辑的推理，故它可以作为数学中严格证明的工具.

⑥公理数学分支中不需经过逻辑论证而确认它的正确性，并可以用它论证命题，公理必须满足无矛盾性，独立性和完备性三个条件.

⑦定理和推论是由前提和结论两部分组成的一个数学命题，客观存在的真实性完全可以经过严格的推理来确认.

（3）数学理论结构的逻辑体系，是以上七种数学思维形式一环连接一环形成的单向有序的逻辑结构链，如下图3所示：

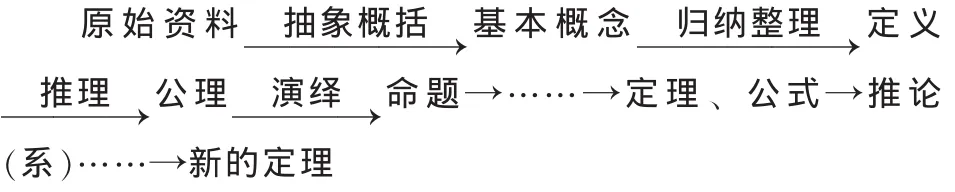
图3

例3 欧几里德几何学和非欧几何学公理化体系：

公元前300年古希腊数学家欧几里德在总结了大量已有的几何知识的基础上，将人们公认的一些几何知识、点、线、面、角、圆等定为几何学基本概念，并把当时人们公认的一些几何知识列成定义和五条公理总结成一套几何学理论的演绎体系并著书取名为《几何原本》，许多年后人们发现欧几里德的公理化系统并不完善，更为完整的几何学公理系统是在19世纪末由德国数学家希尔伯特完成，他改善了欧氏几何学的第五公理，建立了非欧几何，非欧几何学是从公理出发的纯粹演绎系统，形成了近代几何学的公理化体系结构.

随着社会实践活动向广度和深度上发展数学公理化方法不但可以研究具有确定因果关系的确定性数学问题，还可以研究不具有确定性因果关系的随机性数学问题.

例4 用公理化方法建立概率论的公理化体系（Ω、F、Р）.

早期概率论对求解古典型几何型概率问题得出一些结果.但有很大的局限性，碰到比较复杂的随机事件就无能为力，甚至出现像贝特朗奇论的怪现象，使得当时不少人对概率论的科学性产生了怀疑.上世纪20年代以柯尔莫哥洛夫为首的一批前苏联数学家，用公理化方法建立了概率论的公理化体系简记为（Ω、F、Р）它为概率论奠定了严密的数学理论基础，推动了概率论的飞速发展.