潜艇内部平面舱壁极限承载能力分析

蔡少俊，马建军，许 兵，刘 勇，胡大炜

(武汉第二船舶设计研究所，湖北 武汉 430064)

0 引言

潜艇内部平面舱壁是潜艇结构的重要组成部分，其主要用途是将耐压船体分割成不同用途的舱室，同时还对耐压壳体起支撑作用等。在正常工况下，内部平面舱壁结构主要承受来自耐压壳板的面内载荷，而在舱室破损进水工况下，舱壁将主要受到横向载荷作用。在破舱工况下，内部平面舱壁为一次性承载结构，故按弹塑性设计。

潜艇平面舱壁属典型的板架结构，由于弹塑性计算的复杂性，理论分析一般将其分解为三级构件分别计算，即舱壁板、垂直梁以及水平大梁。近年来，随着有限元技术的发展，考虑复杂边界、组合载荷的机构整体计算越来越多。文献［1］提出了有平台支撑的新型平面舱壁结构，并进行了极限承载能力的研究;文献［2］针对潜艇内部平面舱壁的设计现状进行了分析，作出了相关的补充和完善;文献［3］研究了潜艇首端耐压平面舱壁构架的计算方法，引入了计及剪力影响的周边固定系数方法;文献［4］对于潜艇平面舱壁板稳定性校核时外载荷的取值进行了分析。

上述分析计算很少给出结构破坏的机理研究，本文利用非线性有限元软件Marc，对潜艇内部平面舱壁结构进行了材料非线性和几何非线性的双重非线性分析，研究了舱壁结构的破坏机理，分析了其极限承载能力，并与简单梁的破坏机理及极限承载能力进行了对比分析。

1 非线性有限元计算

1.1 有限元模型

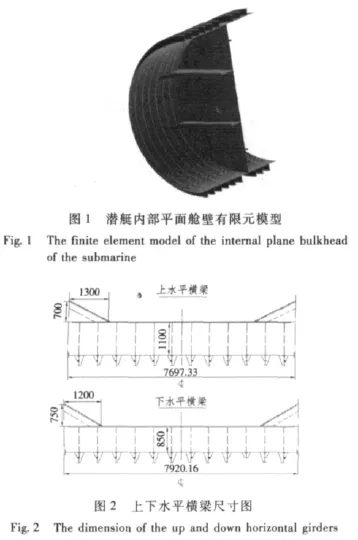
利用MSC.Patran/Marc对典型潜艇内部平面舱壁进行模拟和分析。其中，利用Marc双线性薄壳单元(138，139号)模拟耐压壳板、舱壁板、横梁腹板、肘板腹板、舱壁板加强材腹板，而耐压肋骨、防挠材、舱壁加强材面板采用Marc薄弹性或非线性梁单元(52号)。为保证非线性计算精度，单元大小划分为50 mm×50 mm，最终模型单元总数为61 438个，节点数为58 403个，见图1。此外，还分别单独模拟计算了舱壁上下水平横梁，其尺寸见图2。

1.2 双重非线性

1)材料非线性

耐压壳板、耐压肋骨、防挠材和舱壁加强材面板采用弹性材料，弹性模量E=1.96E5 MPa，泊松比μ=0.3。舱壁板、横梁、肘板、加强材腹板采用弹塑性材料。材料初始屈服准则采用Von Mises准则;利用关联流动准则定义塑性应变增量的分量和应力分量，以及应力增量分量之间的关系;硬化定律为各项同性硬化。Marc非线性计算要求专门设置材料塑性范围内的应力－应变曲线，如图3所示。

2)几何非线性

考虑结构几何非线性，Marc中设置为基于大变形、小应变的更新拉格朗日方法。由于舱壁处在静水压力作用下，还需设置跟随载荷，考虑载荷刚度效应。使用该设置后，会形成跟随力刚度，可对刚度矩阵产生附加贡献，从而改善收敛性能。

1.3 工况和求解设置

1)工况定义

潜艇破舱进水时，舱壁承受来自破损舱室一侧的海水横向压力，因属一次性承载，此时只要求在救生深度下或水面抗沉性设计压力下舱壁结构处于弹塑性设计状态，以最大限度利用结构的极限承载能力，减小构件尺寸和减轻结构重量。破舱工况载荷示意图如图4所示。舱壁计算压力取为1.5 MPa，救生舱室端固定约束，破损舱室端为自由端。通过试算确定极限载荷发生的大致载荷区间，再以此区间为界，将加载过程定义成2个加载工况，分别合理设置2个加载工况中的控制参数，以准确取得极限载荷值。

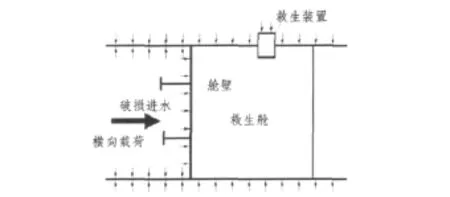
图4 破舱进水后的外压工况Fig.4 The loading case of the slack bulkhead

2)求解选项设置

Marc中将非线性问题的模拟计算过程分为多个载荷步增量，经过多次迭代找到给定载荷增量的满足收敛条件的解，所有载荷增量的响应和就是非线性问题的近似解。通过自动步长加载策略，平衡迭代采用完全Newton-Raphson算法，收敛测试采用基于最大残余载荷与最大反力之比不大于0.1的残差准则。

2 极限承载能力分析

2.1 水平横梁破坏机理分析

目前潜艇设计规范对水平横梁极限载荷的计算是基于三塑性铰破坏机构的原理，按单跨梁极限载荷的计算方法进行理论计算。要求跨端和跨中弯矩值都达到塑性值，即满足如下关系式［5］:

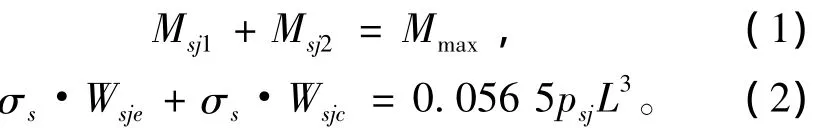
式中:psj为塑性极限载荷;L为梁跨长;Wsje和Wsjc分别为梁跨端塑性剖面模数和跨中剖面模数。

分别按规范［6］理论计算公式和非线性有限元法计算上下水平横梁的极限载荷值，计算结果见表1，上、下水平横梁塑性应变扩展图见图5和图6。从表1可以看出，有限元结果低于理论计算结果，并且差异较大。主要原因是近似理论将梁的弹塑性区退化为1个截面(端部和跨中)，从而提高了梁的刚度，使计算出的极限载荷偏大。此外，对于高腹板横梁，不计及剪力和轴力的影响，也使得极限载荷偏大。

表1 水平横梁极限承载压力值表Tab.1 The table of the ultimate bearing pressure of the up horizontal girder

1)上水平横梁

0.64 MPa时，横梁腹板跨中和跨端靠近舱壁板处出现较明显的塑性铰点。随着载荷增大，沿腹板高度向上急剧扩展，肘板趾端出现塑性铰，并沿着肘板长度方向向跨端扩展;0.94 MPa时，跨中和跨端形成贯穿的塑性铰。但由于肘板对横梁仍具有加强作用，横梁并没像典型单跨梁形成三塑性铰机构后失去承载能力;1.20 MPa时，肘板趾端处塑性铰扩展至跨端，形成沿腹板肘板长度方向贯穿的塑性铰，肘板失去加强作用，横梁达到承载极限。

2)下水平横梁

0.64 MPa时，横梁腹板跨中底部、跨端底部和肘板趾端出现较明显的塑性铰点。随着载荷增大，腹板跨中塑性区沿腹板高度向上急剧扩展，肘板趾端塑性区域沿腹板高度向下迅速扩展;0.99 MPa时，跨中首先形成上下贯穿的塑性铰;1.37 MPa时，肘板趾端也形成上下贯穿的塑性铰，肘板失去对横梁的加强作用，下水平横梁形成了三铰机构，达到了承载极限。

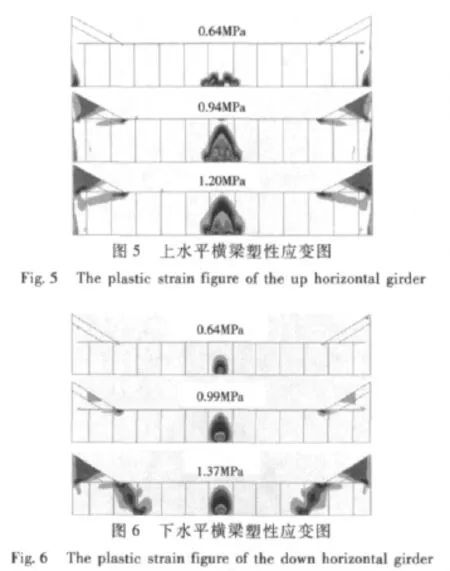
比较上、下水平横梁的塑性铰扩展情况可知:上、下横梁都是首先在跨中形成贯穿的塑性铰;随着载荷增大，肘板处腹板形成贯穿的塑性铰，横梁失去端部转角约束，水平横梁形成典型的单跨梁三塑铰机构，导致结构失去承载能力。

对于高腹板短梁，腹板剪力比较大，故横梁的破坏出现在腹板的剪切屈服区，亦即发生腹板的剪切破坏。其中，跨端和肘板处腹板中形成剪切塑性铰区，跨端和肘板趾端翼板、跨中腹板中形成弯曲塑性铰。

对于下水平横梁，肘板趾端处截面形成贯穿的塑性铰，等效于水平横梁最终形成了跨度缩小的单跨梁结构，提高了横梁的承载能力。因而可以预测，合理设置肘板，可以改善水平横梁的极限承载能力。

2.2 舱壁应力、变形

选择舱壁外表面，在0.64 MPa时，舱壁的Von Mises应力分布见图7所示。肘板面板、防挠材与艇体结合处，以及舱壁板加强材与艇体结合处有应力集中现象。对于舱壁板，可见垂直加强材区域应力较大，即垂直加强材是主要承载构件。对于水平横梁，肘板趾端处腹板应力较大，跨中截面为典型的工字梁倒三角形线性应力分布，截面中性轴区域应力较小。

1.41 MPa时，舱壁板变形如图8所示。最大变形发生在舱壁板中部，而上、下水平横梁处舱壁板变形基本相当，说明上、下水平横梁对舱壁的支撑作用相当。可知，不能由变形来判断舱壁的破坏是由哪根横梁丧失承载能力所致。

2.3 平面舱壁破坏机理分析

取舱壁的中性面，分析上下横梁塑性应变随载荷增大的扩展状况。0.64 MPa时，舱壁塑性应力分布图如图9所示，上、下横梁肘板，及上水平横梁跨中翼板边缘出现较明显的塑性铰点。

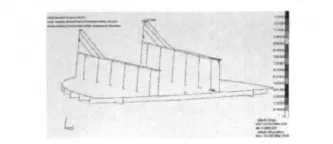
图9 0.64 MPa时舱壁中性面塑性应变图Fig.9 The plastic strain graph of the middle shell of the bulkhead when the pressure at 0.64 MPa

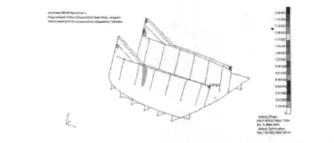
图10 0.95 MPa时舱壁中性面塑性应变图Fig.10 The plastic strain graph of the middle shell of the bulkhead when the pressure at 0.95 MPa

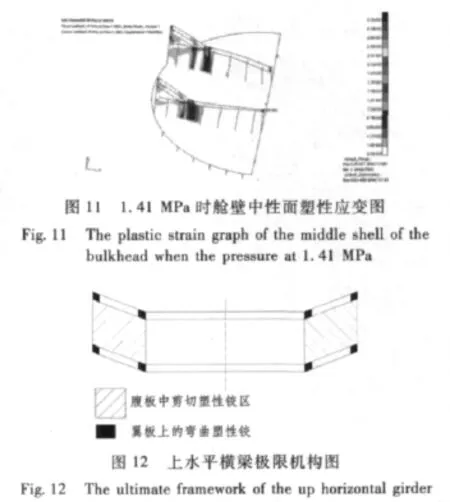
0.95 MPa时，下水平横梁肘板趾端处截面出现沿腹板上下贯穿的塑性铰点，如图10所示。紧接着，上水平横梁肘板趾端处截面也迅速出现贯穿的塑性铰点。随着载荷增大，上水平横梁塑性区域逐渐向跨端发展，整个肘板沿肘板长度方向出现贯穿的塑性铰。到达1.41 MPa时，跨端也形成贯穿的塑性铰，此时，上水平横梁与耐压壳体失去连接作用，等效于横梁端部简支，且肘板对横梁失去加强作用。由于在上水平横梁跨端和肘板趾端均形成塑性铰，横梁形成不稳定的四塑性铰机构。由塑性铰理论，塑性铰处将产生无限大的变形，上水平横梁失去了承载能力，使舱壁失去横梁的支撑作用。舱壁板构件变形和应变将迅速增大，应力发生卸载，即上水平横梁的屈服最终导致了舱壁的破坏。1.41 MPa时，塑性应变图如图11所示，最后形成的四塑性铰机构，其简化等效图如图12所示。

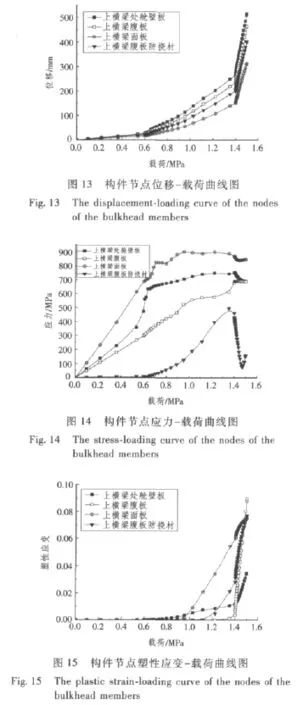
选择上水平横梁典型位置节点，绘制位移－载荷曲线，应力－载荷曲线，塑性应变－载荷曲线，如图13～图15所示。

由上水平横梁典型位置节点位移－载荷曲线，应力－载荷曲线，塑性应变－载荷曲线，可知在1.41 MPa后典型节点位移和塑性应变剧烈变化，应力出现卸载现象，表明上水平横梁达到了极限承载能力。

很明显，舱壁整体与单根横梁破坏机理有一定的区别，且舱壁整体承载能力较单根横梁有了很大的提高。主要原因是，对于舱壁整体，随着载荷增大，上下横梁相互影响地承担着对舱壁的支撑作用，导致单根横梁与舱壁横梁跨端及肘板处塑性铰点扩展和分布有差异。

另外，舱壁横梁并没有像单根横梁那样形成三铰塑性机构，而是形成了四塑性铰机构。其中，跨端和肘板区域腹板形成剪切塑性铰区，跨端、肘板趾端翼板形成弯曲塑性铰，而跨中腹板并未像单根横梁形成弯曲塑性铰区。主要是由于横向载荷作用于舱壁板，板弯曲产生中面拉力即膜应力，这将很大程度上减小板的弯曲应力，尤其是弯曲应力最大的跨中截面。因而跨中腹板与舱壁板之间的弯矩值减小，导致横梁跨中腹板截面弯曲塑性铰未形成。

3 结语

1)利用Marc双重非线性有限元计算分析，结合板梁塑性理论，可以有效地预报潜艇内部平面舱壁的极限承载能力;

2)对于有肘板加强的单根梁，其破坏机理是最终形成典型的三塑性铰机构;

3)对于潜艇内部平面舱壁，由于上下水平横梁相互影响地支撑着舱壁结构，其承载能力较单根梁有所提高，其破坏机理也变得更复杂。最终上水平横梁形成不稳定的四塑性铰机构，失去对舱壁的支撑作用，舱壁达到承载极限。

［1］黄晓明，吴梵.潜艇内部有平台支撑的平面舱壁极限承载能力非线性有限元分析［J］.船海工程，2006，172(3):23－25.HUANG Xiao-ming，WU Fan.Non-linear FEM analysis on ultimate bearing capacity of plane bulkhead supported by inside deck in submarine［J］.Ship ＆ Ocean Engineering，2006，172(3):23 －25.

［2］黄镇熙，李铭，伍莉.潜艇内部平面舱壁设计研究［J］.舰船科学技术，2009，31(12):3 －7.HUANG Zhen-xi，LI Ming，et al.Research of submarine intornal plane bulkhead design［J］.Ship Science and Technology，2009，31(12):3 －7.

［3］曾革委，李科俊.潜艇首端耐压平面舱壁构架设计计算方法［J］.舰舶科学技术，1998，20(2):15 －22.

［4］罗斌，马聘，等.潜艇耐压艇体内部平面舱壁稳定性校核外载荷的分析［J］.舰船科学技术，2002，24(4):9－11.LUO Bin，MA Cheng，et al.External loading analysis for submarine plane hatch wallboard stability verify［J］.Ship Science and Technology，2002，24(4):9 －11.

［5］许辑平，等.潜艇强度［M］.北京:国防工业出版社，1980.

［6］GJB/Z21A－2001，潜艇结构设计计算方法［S］.