垂直相关仪测量高速目标深度的仿真分析
2012-10-20岳剑平李宏伟
岳剑平,尚 超,李宏伟
(91388部队,广东 湛江 524022)
0 引言
高速射流喷射在推进器管壁和水介质上,产生结构振动噪声和气泡脉动噪声。文献[1]讨论了沿深度方向机动的喷射航行体辐射噪声机理,其中高频分量以振动噪声为主,对单水听器信号自相关提取“海面反射—直达声”时延差产生相关峰展宽效应。这种时延参数估计的多普勒效应,增大了高速目标的深度测量误差,于是考虑采用垂直相关仪的测量方案,即利用垂直布放的小尺度双阵元对目标俯仰角进行估计,并通过解算模型对目标深度进行测量。
1 垂直相关仪目标深度测量原理
参见图1,假设目标水平距离R为先验值,根据直达声俯仰角θ,可求解目标深度:
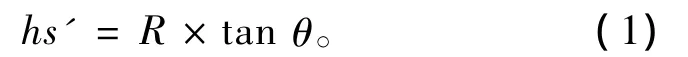
近程直达声以平面波方式传播,不难推得:
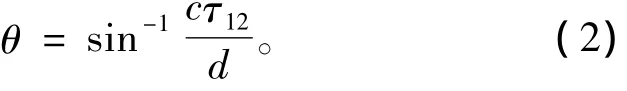
式中:c为声速;τ12为相关仪双阵元测得的传播时延差;d=d2-d1为阵距。
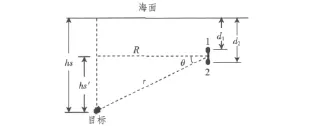
图1 垂直相关仪目标深度测量几何示意图Fig.1 The geometric sketch of the depth measurement
2 信号相关特性及多普勒容限
根据文献[2],白噪声经过1个理想带通滤波器,产生带通型限带白噪声,具有均匀的谱结构,其功率谱密度表示为:

式中:W为角频率带宽;ω0为通带中心角频率;S0为常数,代表单位角频率带宽的噪声功率。应用维纳-辛钦定理,可以导出对应的信号相关函数:
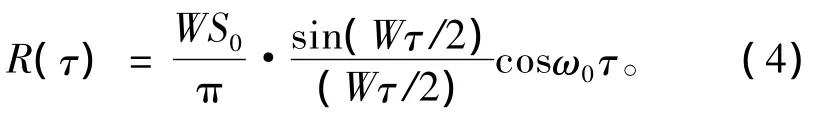
其中,cosω0τ可理解为载频信号,相关峰值表示噪声总功率。
包络受到辛格函数sinx/x的调制,主包络宽度为4π/W=2/B,其中B为信号带宽,以Hz为单位。主极大相关峰的根部取值为0,宽度即为载频的1/4周期,其时间分辨力为:
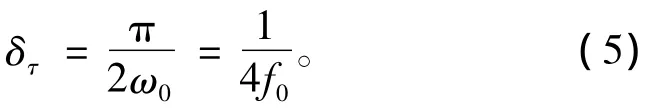
式中:f0为通带中心频率,Hz。当W=ω0或B=f0时,主包络内只含有惟一的主极大相关峰。这种情况下,即使背景噪声较大,也不太容易发生将副包络次极大误判为主极大的错误。取B=f0=20 kHz,于是δτ=12.5 μs。若采样频率设置为500 kHz,或结合内插算法,信号相关时延差估计精度应当优于10 μs。
目标声源与测量基阵作相对运动时,接收点的信号波形与辐射波形相比较,在时间上将被压缩或拉伸,这一现象称为多普勒现象。多普勒现象将导致互相关系数降低,称作互相关失配。
根据文献[3],基阵联线的中垂线上,多普勒的影响最为显著。如图2所示,对于小尺度基阵,认为R>>d,于是阵元接收信号的波形时间关系有:
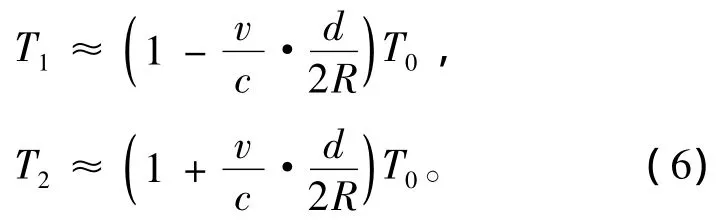
式中:T0为辐射波形的时间长度;v为目标沿深度方向运动速度;c为声传播速度;R为目标水平距离。式(6)表明,阵元1的信号长度T1被压缩,阵元2的信号长度T2被拉伸。
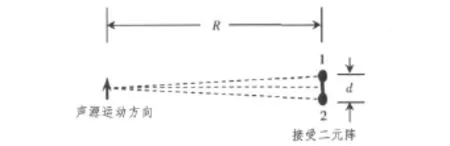
图2 二元基阵测量原理示意Fig.2 The sketch of the principle with two sensors
信号长度的差值表示为(T2-T1),一旦该值大于噪声信号的时间相关半径,即认为2个接收信号不再相关。依据主极大相关峰宽度,给出互相关的多普勒容限不等式:
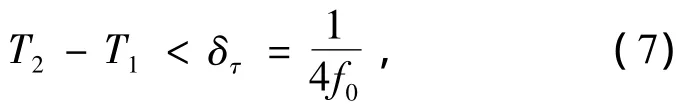
化简为:
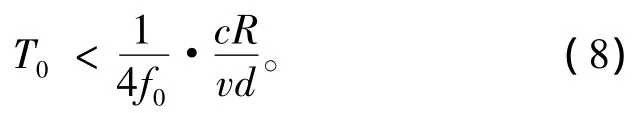
多普勒容限表现为互相关积分时间T0受到限制。值得注意的是,互相关积分时间与目标距离呈正比例关系,即近距离目标的积分时间更短。
为便于仿真观察,不妨取信号频段10~30 kHz,另令c=1 500 m/s,R=350 m,v=300 kn和 d=3 m,于是 B=f0=20 kHz,计算得 T0<14.6 ms。时域信号仿真如图3所示,2个阵元的差值信号在15 ms以内,反映了幅度线性递增的规律,表明阵元之间信号相关度随时间减弱的趋势,与理论值吻合一致。
3 浅海多途信道冲激响应结构
目标的当前位置(深度)记成hs,仅考虑海面海底一次界面反射的情形。由于目标高速运动,当阵元接收到当前时刻直达声的同时,还将接收到此前某一时刻“先发后至”的海面反射声,和另一时刻“先发后至”的海底反射声,三者时间上重叠,但互相独立而分别形成信号和干扰。为便于仿真观察,不妨假定海面反射干扰来自目标hs+10 m深度,而海底反射干扰来自目标hs+20 m深度,均含相应的多普勒信息。
采用极短脉冲可测试浅海信道的冲激响应函数,如图4所示。仿真不仅反映了上述3个信号或干扰的叠加现象,同时还给出了直达声“副本”所形成的一次界面反射的时延结构。其中海底反射“副本”的时延较大,并且随目标深度减小而进一步增大。
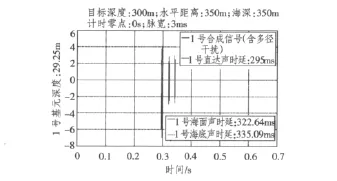
图4 多途信道的时延结构Fig.4 The time delays of the multi-path channel
4 多途信道信号互相关多普勒仿真
对于高噪目标,近程接收信噪比很高,仿真可不考虑环境背景噪声。互相关积分时间取20 ms,并限定目标俯仰角不大于45°。阵距设为1.5 m,相关延迟域观察窗选取±1 ms,因此海底反射的“副本”信号被排除在外,大多只含有4个信号,包括了直达声、海面反射“副本”和2个多途干扰,其中仅前2个信号有可能相关。当不考虑多普勒效应时,这2个相关信号将产生(负向的)交叉相关峰。
如图5所示,4个信号按镜像原理,在深度方向上由深及浅,分别形成了1个真实的直达声源和3个反射虚源,依序为海底反射干扰、直达声信号、海面反射信号和海面反射干扰。一般地,负轴最小延迟的相关峰即代表直达声信号。图中,目标接近海面且多普勒取0 kn,因此合成信号观察到了(负向的)交叉峰现象。当设置目标速度150 kn时,该交叉峰消失。
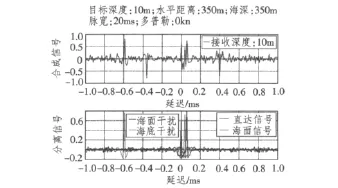
图5 无运动多普勒的相关交叉项现象Fig.5 The cross-item phenomenon of the correlation without Doppler
利用仿真还可观察信号互相关的多普勒失配效应。在图3仿真条件下仅改变积分时间长度,发现信号脉宽T0=15 ms的质量较好,当T0≥25 ms后,互相关失配开始趋于明显。图6仿真表明,延迟域观察窗不仅排除了海底反射“副本”信号,而且还排除了海底反射干扰相关峰。由于目标速度高,因此无法观察到交叉峰现象,且积分时间大于式(8)理论值一倍时,相关系数损失约50%。
5 目标深度测量误差分析
根据式(2),仅考虑测时误差,推导俯仰角测量误差为:
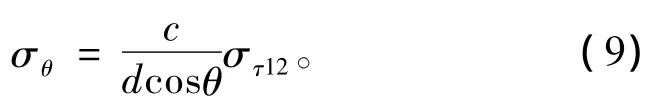
式中:στ12为时延差估计精度。取c=1 500 m/s,d=1.5 m,στ12=10 μs,θ最大取值 45°,计算得 σθ≤0.0141 rad,即 0.81°。
根据式(1),目标深度测量误差的传递公式为:
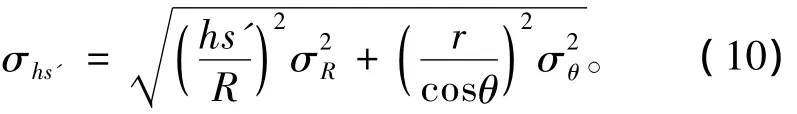
观察式(10)根号下第一项,通常hs'≤R,由此引起的误差最多与水平测距误差相当;观察根号下第2项,与目标斜距r呈正比例关系,考虑最大的θ=45°,其值不大于 2Rσθ。
相关仪测量阵元铅垂布放,当安装倾斜角出现0.4°偏差,即2个阵元声学中心的水平偏差为1 cm时,按R=350 m且θ=45°进行换算,引起目标深度的测量偏差约3.5 m。
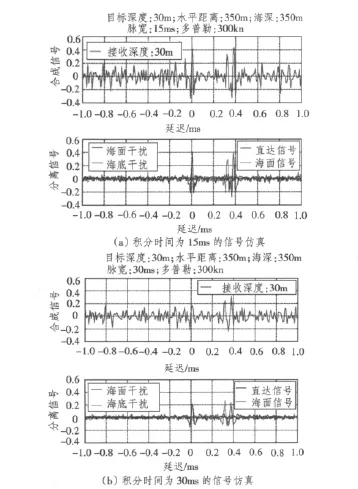
图6 互相关的多普勒容限仿真Fig.6 The simulative result of the Doppler tolerance of the cross-correlation
根据式(2),阵距误差引起的角度偏差为:
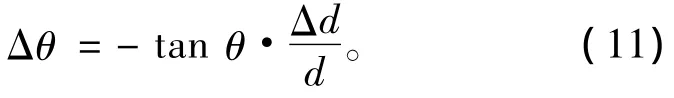
阵距校准后的偏差Δ d/d取1.5‰,如d=1.5 m的情况,声学中心的阵距偏差控制在±2.25 mm以内。
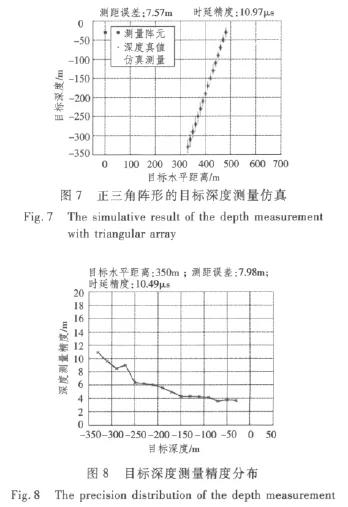
忽略测量的系统偏差,仅对随机误差进行理论和仿真分析。假设利用3个矢量传感器基阵,布设呈基线600 m的正三角阵形,对目标的水平面定位精度σx和σy约为5 m,换算水平测距误差σR约为7 m。每个测量基阵均安装垂直相关仪,目标位于阵形中心点,距离各基阵约350 m,而目标布放深度与此相当,即俯仰角最大约45°。根据式(9)和式(10)进行误差综合,目标深度测量误差不大于12.1 m。
设置相关仪阵距1.5 m,布设深度30 m。图7是其中1个相关仪测量目标深度的仿真结果,上升轨迹稍有倾斜,是为了便于观察深度测量的散布情况。图8是上升轨迹无倾斜时的误差统计结果,表明测量精度与理论分析一致。
6 结语
垂直相关仪用于目标深度估计,主要受浅海信道多路径干扰。研究表明,互相关延迟域的相关峰结构实际上具有空间映射关系,直观地反映了直达声目标和界面镜像的空间分布规律,并且多普勒效应有助于降低多途交叉干扰。仿真结果表明,在给定的诸多条件下,垂直相关仪的目标深度测量误差大约控制在10 m以内。
[1]岳剑平,孙良义,贾建龙.喷射航行体辐射噪声机理分析[J].舰船科学技术,2008,30(6):155 -156.YUE Jian-ping,SUN Liang-yi,JIA Jian-long.Mechanism analysis of radiated noise for spraying vehicle[J].Ship Science and Technology,2008,30(6):155 -156.
[2]朱华,黄辉宁,李永庆,梅文博.随机信号分析[M].北京:北京理工大学出版社,1990.227 -229.ZHU Hua,WANG Hui-ning,LI Yong-qing,MEI Wen-bo.Random signal analysis[M].Beijing:Publishing of Beijing Institute of Technology,1990.227 -229.
[3]惠俊英.水下声信道[M].北京:国防工业出版社,1992,96-98.
