连续波体积混响声强仿真
2012-10-20崔剑锋安天思马忠成朱练军
崔剑锋,安天思,马忠成,朱练军
(大连测控技术研究所,辽宁大连116013)
1 概述
连续波理论和技术最初应用在雷达上。连续波雷达在短距离应用中能够提供较高精度的速度和距离信息,在工业领域发展出无接触式测量技术,在交通领域里有防撞雷达的出现。连续波技术有着独特的优点,例如测量精度高、简单小巧、带宽大、平均发射功率低、被截获的概率小。连续波技术在声呐中的应用正日益引起水声领域科研人员的注意。
对于主动声呐而言,除了受到各种噪声的影响,还受到混响信号的影响,而且很多情况下混响是主要的背景干扰,在连续波声呐技术中这一问题尤为突出。
按照传统水声学著作中给出的计算混响等效平面波混响级理论公式 (以体积混响为例)
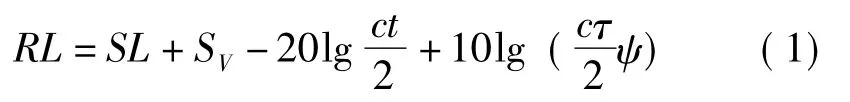
能够得出,混响声强与入射波强度、发射信号的脉冲宽度 (式中τ表示脉宽)、发射-接收换能器的组合指向性束宽等量成正比[1]。
在发射连续波时,发射信号的脉冲宽度扩大到无限长,计算混响声强的理论模型将不再适用,推导出的理论公式也不再成立,其结论无法对连续波的等效平面波混响级做出指导。
需要指出式(1)推导之前所做的5条假定[1-2]:
1)直线传播,不考虑除球面衰减外的其余衰减。
2)任一瞬间位于某一面积或体积的散射体的分布是随机均匀的。
3)散射体密度甚大,认为任一面元或体元都有很多散射体。
4)忽略多次散射,即混响所产生的混响。
5)脉冲时间足够短,以至于可以忽略面元或体元尺度范围内的传播效应。
由于存在第5条假设,式(1)得到的理论公式事实上只能适用于短脉冲波的混响声强计算,针对连续波理论,须另作考虑。
应连续波声呐技术发展的需求,本文从体积混响入手,详细推导了连续波混响声强的计算,并借助计算机做了数值计算,为相关的连续波声呐技术提供参考。
2 推导
海洋中大量的散射体按各自规律分布在海水中,其距离发射换能器与接收换能器的距离有近有远,产生的散射波不会同时到达接收器。理想情况下,考虑海水中均匀分布着大量散射体,设发射器与接收器的指向性函数分别为 b(θ,φ)和 b'(θ,φ),S'V为距离产生散射的单位体积1 m处的反向散射声强度Iscat与入射声强度Iinc之比,即

S'V与散射强度SV的关系为
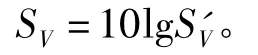
以半径为r的球面的散射声强作为被积函数,可以得到总的散射声强为

在发射连续波的情况下,理想的无穷介质中,理论上即可以认为积分上限取无穷。式中,I0是距离为单位距离处的声强,4πr2是距离为r处的球壳面积。
式(3)经化简得到:
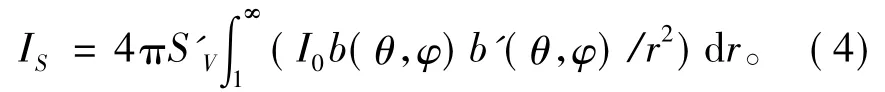
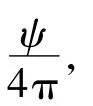
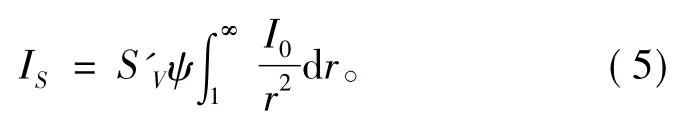
以上推导中,始终没有将I0作为常数提出,其原因正是由于第5条假设。在发射连续波的情况下,I是一个关于时间与距离的函数,如前所述,I0是距离为单位距离处的声强,即

设发射信号是振幅为A,频率为f的余弦波,则有:
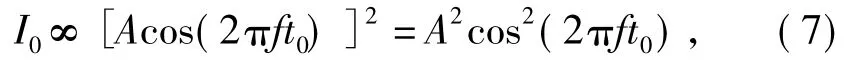
代入式(5)可得:
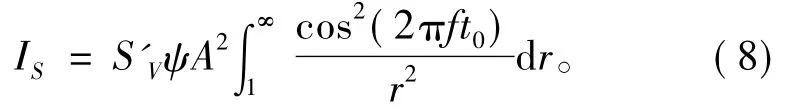
式(8)积分形式可简化为


此类积分的准确计算本文不做讨论,为了简化计算,在已知被积函数振荡收敛到0的情况下,在误差允许时,做如下代换:

式中:T为发射信号的周期;λ为波长。设水中波速为1 500 m/s,进一步化简式 (8),即可得到
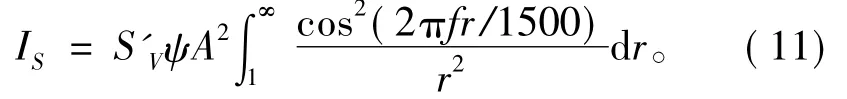
此类积分无法得到解析值,需借助计算机做数值积分。
3 数值计算
在Matlab环境下进行数值计算[4]。需要注意积分步长的选择,在某一确定半径内,积分点数应满足香农采样定律:

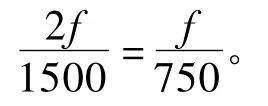

化简得到:

在满足式(14)的前提下,在Matlab中利用trapz函数进行数值计算,由于S'VψA2为常数,此处主要计算积分式:
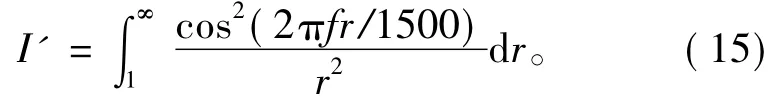
1)f=3 kHz时
在满足式(14)的前提下,绘制频率为3 kHz时I'的积分结果,如图1所示。
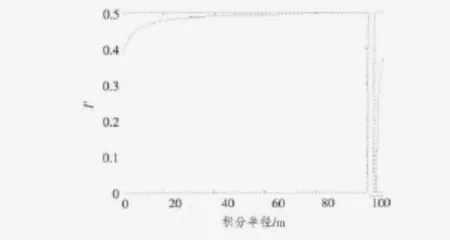
图1 f=3 kHz,积分半径100 m,I'值Fig.1 Frequency=3 kHz,radius=100 m,the value of I'
积分半径增加到500 m,点数不变,仍满足式(14),结果如图2所示。
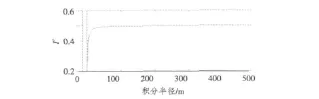
图2 f=3 kHz,积分半径500 m,I'积分结果Fig.2 Frequency=3 kHz,radius=500 m,the value of I'
对图1作放大观察,见图3。

图3 图1的放大Fig.3 Enlarged drawing of figure 1
分析图1~图3,随着积分半径扩大,I'迅速收敛到某一值并做微幅振荡。考虑到实际海水的积分体积有限,且考虑到积分半径大幅增加时积分值的微幅变化,可以认为积分半径取到100时I'的积分值几乎不再变化。即I'在工程意义上近似收敛。
结合图1与图2,可以看出发射频率3 kHz时I'近似收敛于0.5。
2)f=10 kHz时
积分半径取100 m,积分点数10 000,代入式(14),得到:
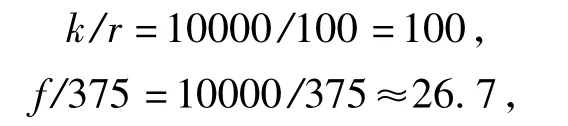
100>26.7,满足条件。积分结果见图4。

结果与频率取3 kHz时较为一致,I'迅速收敛到某一值并做微幅振荡。即能够认为频率取10 kHz时,I'近似收敛。
3)f取其他值时
当f取其他频率时对I'做数值计算 (需要注意满足式 (14)),结果如图6和图7所示。

图6 不同频率下I'取值Fig.6 The value of I'in different frequency

分析图6和图7能够印证前面得到的结论,即在给定的频率下,连续波体积混响场的声强近似收敛。由f=3 kHz和f=10 kHz的分析并结合图能够得出,在频率高于大约3 kHz时的高频频段,简化系数后的混响场声强几乎都收敛至0.5,而在低频频段,需要依据式 (15)进行计算。
表1给出部分频率下I'的近似收敛值。
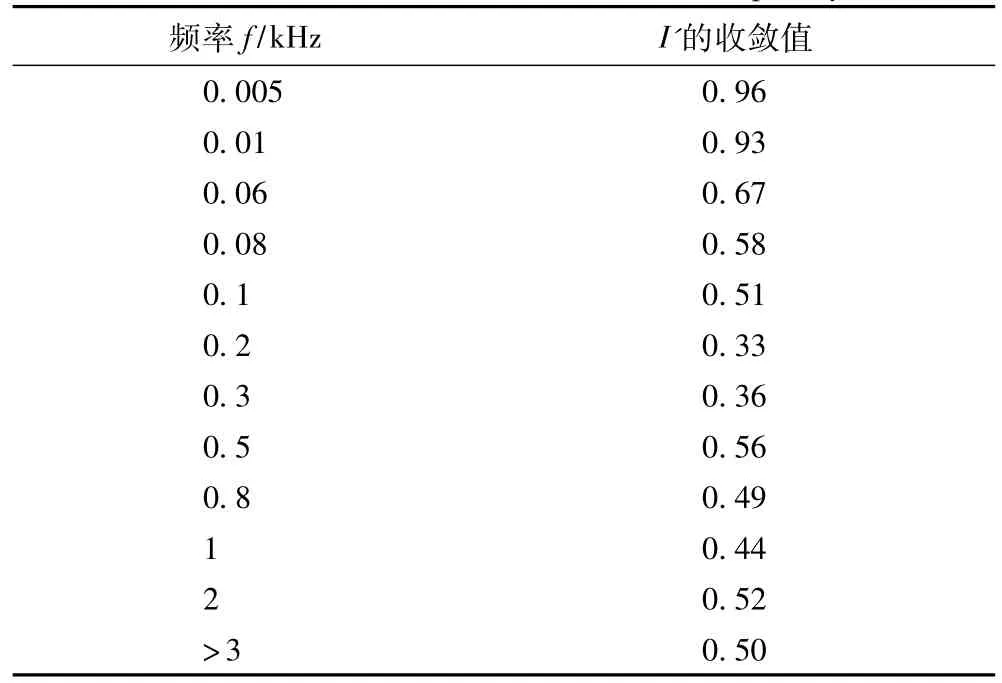
表1 不同频率下I'的收敛值Tab.1 The value of I'in different frequency
4 误差分析
上述分析与计算中不可避免地存在误差,主要原因有以下几方面:
1)时空域同时趋于无穷时的近似代换;
2)积分体积、水中波速等条件的理想化;
3)数值积分时取有限的积分半径;
4)舍入误差;
5)数值计算中步长不能无限小引起的计算误差。
5 结语
综合以上推导及数值实验,能够得到如下结论:
连续波体积混响的混响声强是近似振荡收敛的。收敛值
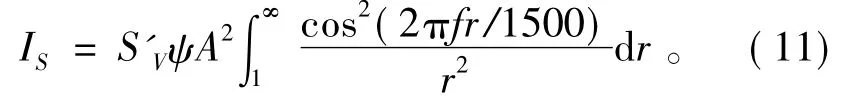
可见收敛值与散射强度、指向性束宽、发射源级、发射频率有关。这一结论与相关论著[1-2]中给出的关于体积混响声强的结论有明显差别。
并且在计算中发现,在频率大于3 kHz的情况下,简化系数后的积分式I'均近似收敛于0.5;而在小于几千Hz的低频频段,各频率下的收敛值具有一定的规律,但并不像高频时的收敛值一样具有较强的一致性,需要依据式 (15)进行计算。
因此,高频情况下,一定的误差限内可认为

根据等效平面波混响级RL的定义,可以得到等效平面波混响级表达式为
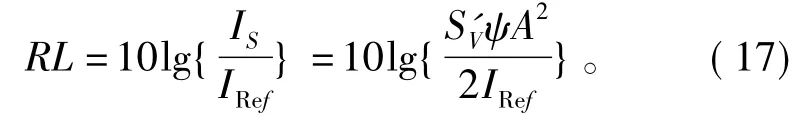
本文结果能够为连续波声呐技术中混响级的计算及实验提供参考。本文的思路也适用于连续波的界面混响分析,能够想见,连续波的界面混响级也应符合振荡收敛的规律,有待于进一步分析论证。此外,本文中表1的研究仍有待进一步完善,对其表现出的规律需作进一步的探究和解释。
[1]刘伯胜,雷家煜.水声学原理[M].哈尔滨:哈尔滨工程大学出版社,2006.
[2]URICK R J.Principles of underwater sound[M],3d edition.Mcgraw-Hill Book Company,New York,1983.
[3]同济大学数学系.高等数学[M].北京:高等教育出版社,2007.
[4]William J Palm III著.MATLAB 7基础教程——面向工程应用[M].黄开枝译.北京:清华大学出版社,2007.
[5]何祚镛,赵玉芳.声学理论基础[M].北京:国防工业出版社,1981.
[6]宋兆基,徐流美.MATLAB 6.5在科学计算中的应用[M].北京:清华大学出版社,2005.
