稳态分数阶Kalman滤波器
2012-10-17孙小君闫广明
孙小君,闫广明
(黑龙江大学a.电子工程学院;b.机电工程学院,哈尔滨 150080)
0 引 言
近年来,随着现代科学技术的发展,在系统分析和集成中越来越要求系统的精确描述。因此分数阶微积分[1-2]也开始逐渐受到关注。文献 [3]给出了分数阶微积分在粘粘性方面的研究;文献 [4]则给出其在分形方面的研究;文献 [5]和文献[6]分别使用分数阶微积分给出了频域和时域的控制算法。然而关于分数阶系统的Kalman滤波的研究却尚属少数[7-9]。在文献 [7-9]中分别通过两种不同的推导方法得到了分数阶Kalman滤波器。
本文将对线性离散分数阶状态空间系统提出一种新的稳态分数阶Kalman滤波器。其推导过程完全不同于文献 [7-9]。仿真例子说明了所提出的滤波器的有效性。
1 问题的提出
考虑如下线性分数阶离散状态空间系统:
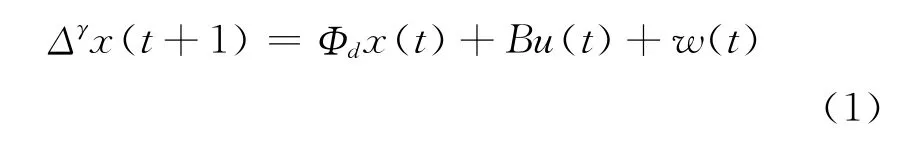

式中t为离散时间;γ为分数阶;x (t)∈Rn为状态;y (t)∈Rm为观测;u (t)∈Rp为已知控制输入;w (t)∈Rr和v (t)∈Rm为白噪声;Φd、B和H 为适当维数的常阵。
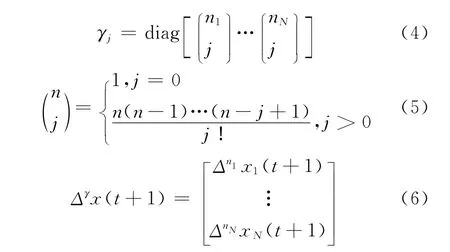
式中n1,…,nN为系统方程的阶数;N 为方程数。
当γ=1,Φd=Φ-I时,可得到通常的整数阶离散状态空间系统:
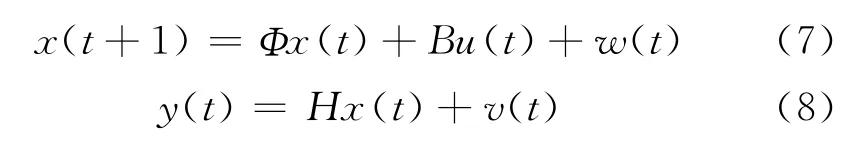
【假设1】w (t)和v (t)为零均值方差分别为Qw和R的相互独立的白噪声。则:
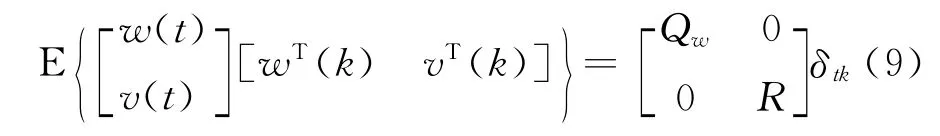
【假设2】x (0)不相关于w (t)和v (t),且有:
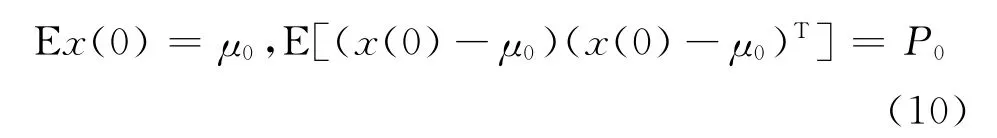
【假设3】系统完全可观且完全可控[2]。
稳态Kalman滤波问题为基于观测 (y (1),…,y (t))求线性最小方差状态滤波器^x (t|t)。
2 稳态分数阶Kalman滤波器
由式 (1)、式 (2)和式 (3)有:
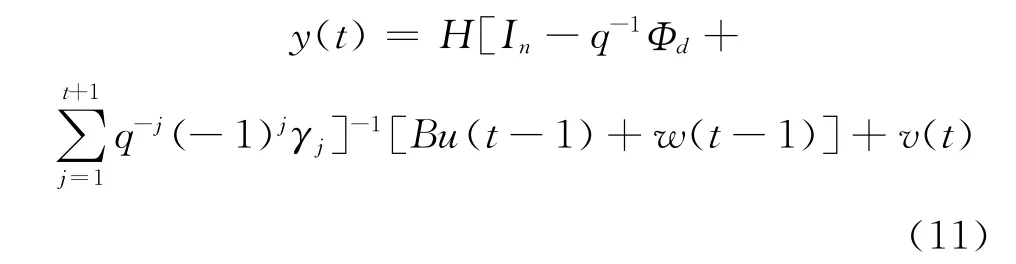
式中In为单位阵;q-1为单位滞后算子,q-1x (t)=x (t-1)。
引入左素分解得:
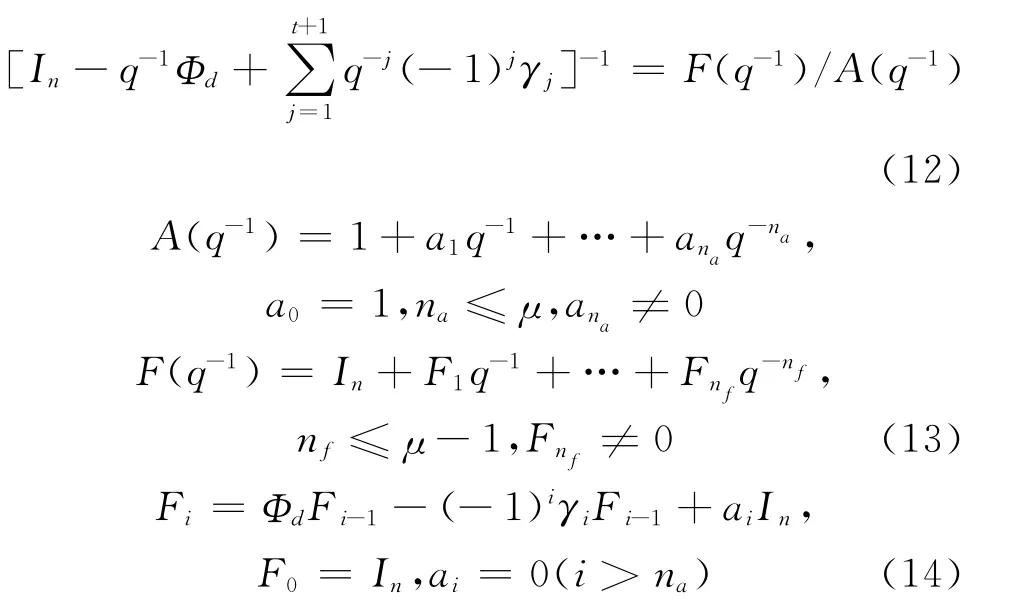
其中qμA (q-1)为Φd的最小多项式。
将式 (12)代入式 (11)得:
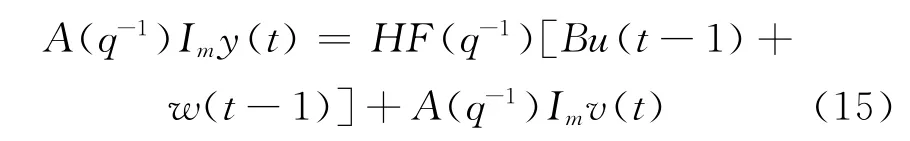
在 (A (q-1)Im,HF (q-1)Bq-1,HF(q-1)q-1)左素且A (q-1)Im和HF (q-1)q-1没有行列式零点在单位圆上的左因式的假设下,应用式 (15)得到CARMA新息模型:
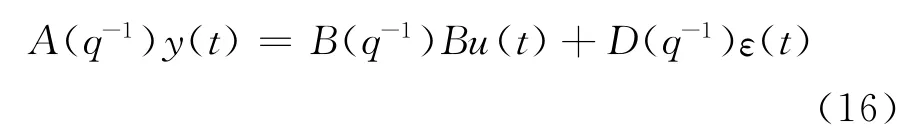
式中B (q-1)=HF (q-1)q-1;D (q-1)为稳定的,D0=Im;新息ε(t)是带零均值方差阵为Qε的白噪声,可得到如下关系:
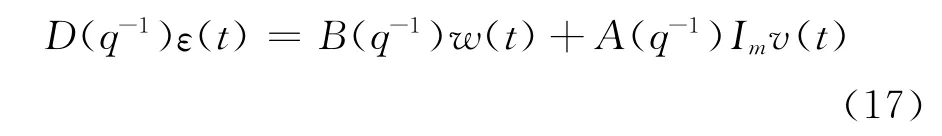
其中D (q-1)和Qε可由 G-W 算法得到[10]。
定理1 对系统 (1)~ (3),在假设1~3下,稳态分数阶Kalman滤波器和预报器为:
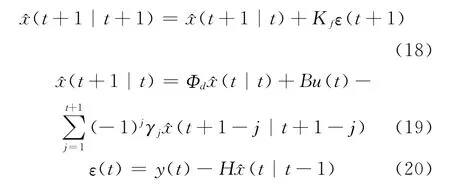
滤波增益为:
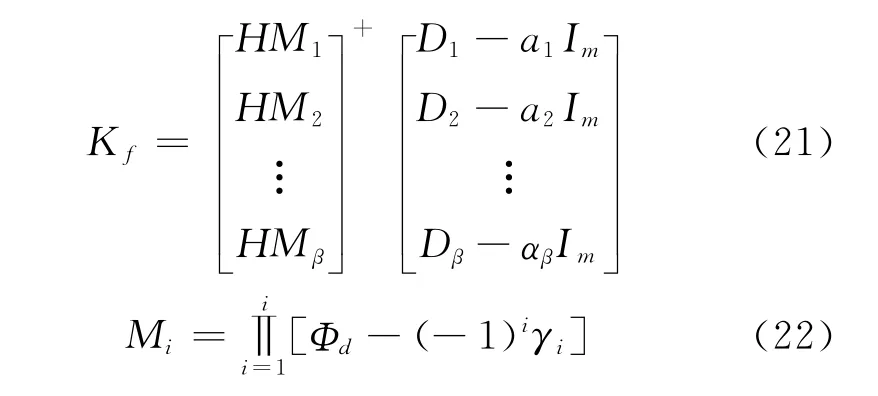
其中矩阵X的伪逆X+定义为X+= (XTX)-1XT。
证明 应用假设2得到稳态Kalman滤波器和预报器存在[10]。
由式 (1)、式 (2)和射影性质得:
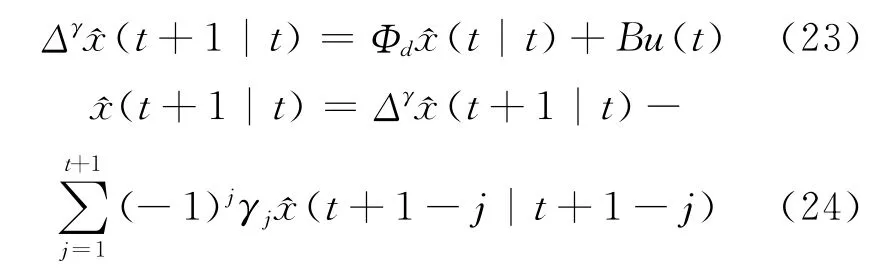
进而有式 (19)。应用射影公式得式 (18)和式 (20)。
应用Fadeeva公式 (12),并应用式 (18)、式(19)和式 (20)有:
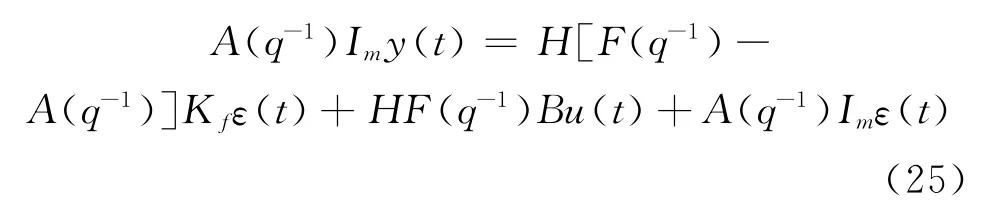
比较式 (16)和式 (25)有:
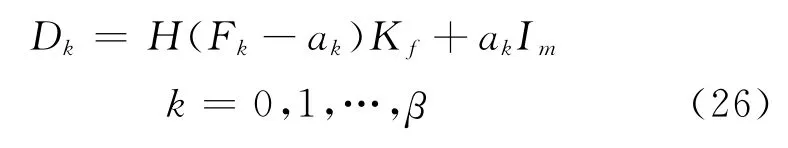
式中Dk=0,k>nd。
由假设3得:
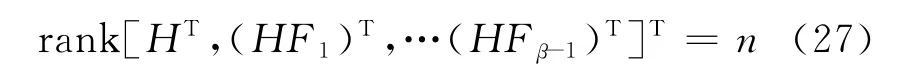
应用反证法得到nf≥β-1。
应用式 (26)得:
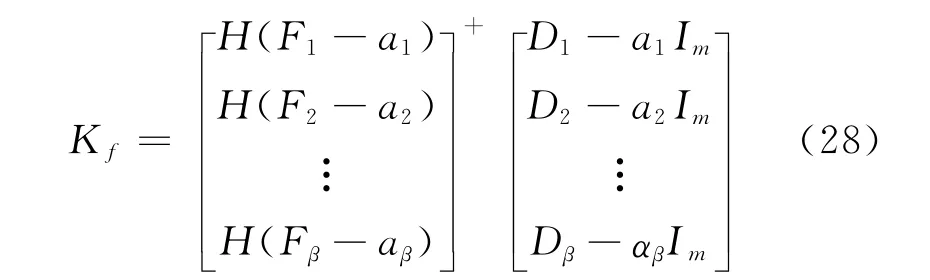
应用式 (14)和式 (28)得到式 (21)和式(22)。证毕。
3 仿真例子
考虑如下带单位阶跃输入的线性离散分数阶状态空间系统:
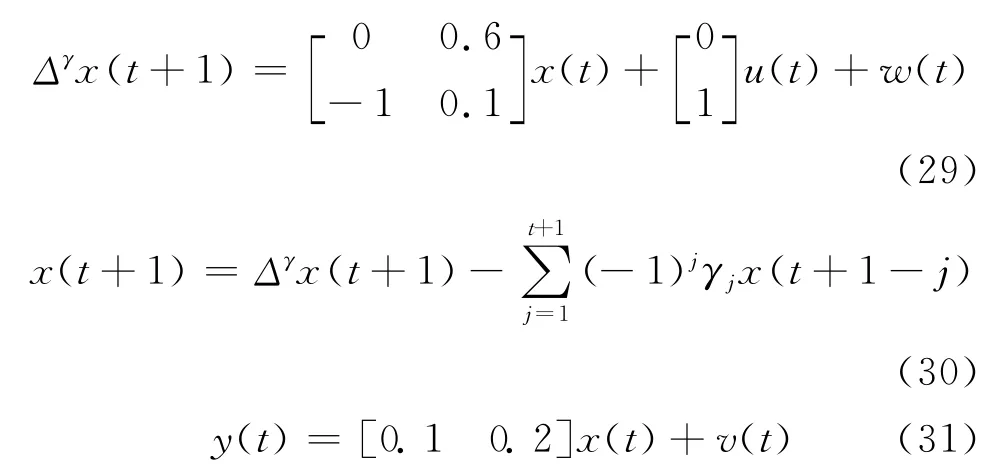
式中γ为分数阶;x (t)∈R2、u (t)∈R、y (t)∈R分别为时刻t的状态、输入和输出;w (t)∈R2和v (t)∈R为带零均值方差阵分别为Qw=和R=0.01的白噪声,n1=0.9,n2=1.1。问题为求分数阶 Kalman滤波器(t|t)。
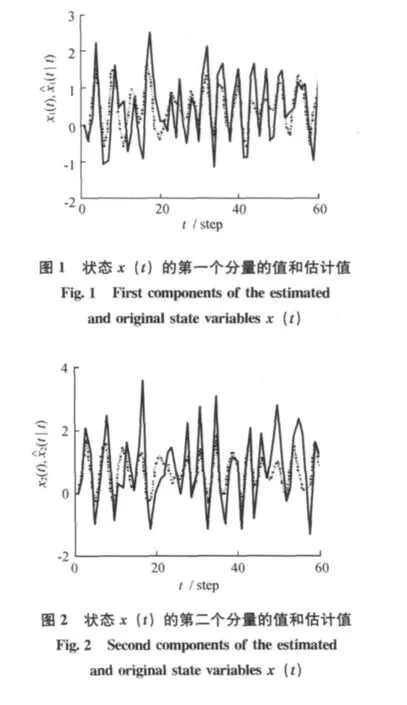
仿真结果见图1和图2。在图1和图2中给出了状态的第一个和第二个分量值与估计值曲线,其中实线表示真实值,虚线表示估计值。从中可以看出状态变量的估计精度较高。
4 结 论
本文对线性离散分数阶状态空间系统提出一种新的稳态分数阶Kalman滤波器。同时给出详细的推导过程。仿真例子表明所提算法的有效性。所提出的结果克服了现有相关文献大多针对整数阶系统研究的缺点和局限性。
[1]K.B.Oldham,J.Spanier.The fractional calculus[M].Academic Press,1974.
[2]汪纪锋.分数阶系统控制性能分析 [M].北京:电子工业出版社,2010. (J.F.Wang.Control performance analysis for fractional order systems[M].Beijing:Publishing House of Electronics Industry,2010. (in Chinese))
[3]R.L.Bagley.Fractional calculus-a different approach to the analysis of viscoelastically damped structures[J].AIAA Journal,1983,21:741-748.
[4]M.Bologna,P.Grigolini.Physics of fractal operators[M].Springer-Verlag,2003.
[5]A.Oustaloup.The crone control of resonant plants:Application to a flexible transmission [J].European Journal of Control,1995,1:113-121.
[6]J.T.Machado.Anaylsis and design of fractional-order digital control systems[J].SAMS-Journal Systems A-nalysis,Modelling,Simulation,1997,27:107-122.
[7]S.Dominik,D.Andrzej.Fractional Kalman filter algorithm for the states,parameters and order of fractional system estimation [J].International Journal of Applied Mathematics and Computer Science,2006,16 (1):129-140.
[8]D.Andrzej,S.Dominik.Adaptive feedback control of fractional order discrete state-space systems[C]//CIMCA-IAWTIC’05,Vienna,Austria,28-30November 2005,1:804-809.
[9]X.J.Sun,G.M.Yan.Fractional order Kalman filter[A].2nd International Conference on Intelligent Control and Information Processing [C].Harbin,China,25-28July 2011,836-838.
[10]Z.L.Deng,Y.Gao,L.Mao,et al.New approach to information fusion steady-state Kalman filtering[J].Automatica,2005,41 (10):1 695-1 707.
