基于时频分析的混沌谐波线性混合信号提取算法

王尔馥，王冬青

（黑龙江大学 电子工程学院，哈尔滨 150080）

0 引 言

自然界中很多现象可以由混沌信号来抽象，混沌现象普遍存在于各个领域中，如保密通信、电子对抗和心电／脑电信号处理等。因此，混沌信号处理理论受到越来越多学者的关注。

研究人员依据混沌信号的特性提出各种从混沌中检测、分离和提取信号信息的方法［1－6］。Leung利用最小相空间体积方法估计嵌入混沌中多项式参数［7］；汪芙平等人利用混沌吸引子固有的几何性质，借助微分流形切空间的概念实现混沌干扰和弱信号分离［8］；Haykin利用人工神经网络方法研究了海杂波 （已被证明为混沌噪声）背景下的小目标信号提取；Short则根据混沌信号可短时预测的特性，利用混沌预测的方法考察了混沌通信系统中信号的提取［9－10］；这些方法开拓了混沌信号处理的新领域，但缺乏系统性，另外有些方法要求比较苛刻，适用性差，而且一般要求都是目标信号远远小于混沌背景信号［11－15］。近年来，时频分析理论逐渐发展起来，其主要解决连续型混沌系统背景中谐波信号的提取问题，根据混沌、噪声与谐波信号不同的时频特性，实现混沌和信号的分离，从而从混沌背景中提取有用信号。在信号不太弱的情况下，提取的效果比较理想。本文针对不同噪声水平下的混沌背景中谐波信号的提取性能进行分析，将小波变换与EMD方法进行比较，找出其适用场合及算法优势。经过仿真实验总结出一种新的谐波信号提取的小波阈值与EMD优势互补的综合方法，并给出优势互补方案的提取步骤。在理论分析之后，进行了大量的仿真实验，并给出了相应的结果与分析。

1 时频分析理论

时频分析方法是处理非平稳信号的一种非常有效的手段，能同时获取信号的时域和频域特性，其中以小波变换方法最为经典。此外，经验模态分解（Empirical Mode Decomposition，简称EMD）作为一种新兴的时频信号处理方法，在某些应用场合下能得到比小波变换更好的性能。

1．1 小波变换

小波变换是一种时频分析方法，于20世纪80年代中后期发展起来。对于给定信号x （t）∈L2（R），其连续小波变换 （CWT）定义为：

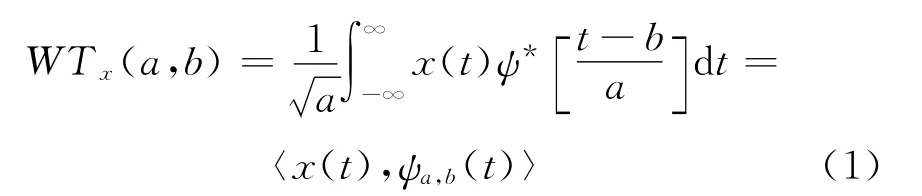
式中a＞0是尺度因子；b是时移因子；ψa，b（t）＝是母小波的移位和尺度伸缩，称之为小波基函数。

小波变换实质上是原始信号与经过伸缩后的小波函数族的相关运算。

1．2 小波阈值去噪原理

基于小波变换的分析过程，实质上是小波分解与重构的过程，由于Daubechies小波基具有连续、正交，且计算机易实现的特性，本文选用Daubechies小波中局部特性和正交特性都很好的db6小波。

由于小波变换是线性变换，小波变换系数是加性的。当选用与信号相匹配的小波进行小波变换时，信号的能量将集中在某些频带的少数稀疏的、幅度相对比较大的小波系数上，而白噪声的小波变换仍然是白噪声，它广泛地分布在各个尺度的时间轴上且幅度不是很大。这样一来，可以设定一个阈值，利用该阈值按照一定的规则对小波系数进行调整。对经阈值调整后的各级小波系数按小波变换的反演算法进行信号重构得到目标信号，这就是小波阈值去噪的理论依据。

1．3 EMD

EMD （经验模式分解）由N．E．Huang等人提出，是一种分析非线性、非平稳信号的有力工具。EMD方法建立在对瞬时频率概念进行深入研究的基础之上，并与相应的Hilbert变换方法紧密相关。通过对非线性非平稳信号的分解获得一系列表征信号特征时间尺度的IMF（固有模态函数），使得每个IMF为窄带平稳信号。IMF必须满足以下两个条件：

1）函数的过零点数目与函数的极值点数目相等或者至多相差1；

2.把好引种和繁殖关。一是在引进种兔时，要做好引种计划，应到有种兔经营许可证的正规种兔场引种，不可到疫区特别是患有兔球虫病严重的或饲养管理条件较差的种兔场引种；选种时应选择外貌符合该品种特征，系谱档案资料齐全，精神良好，行走姿势正确，耳朵转动灵活，被毛光洁，毛短齐密，无皮肤病等的种兔，种兔年龄应选择4～5月龄的青年兔。二是在配种繁殖时，要做好配种繁殖计划，配种时间宜选在1～4月份、8～12月份等阶段，气温较高时应安排在早晨和夜间的8～10点，气温低时可在上午9～10点或在晚上7～9点，配种时期还应避开高温多雨季节；此外，配种前最好先对种兔的粪便进行检测，患有球虫病的种兔不得用于配种繁殖。

2）在任意一点，函数的局部极大值所定义的包络与函数局部极小值所定义的包络均值为0。

只有将信号分解成若干个IMF之和，通过分析各个IMF的瞬时频率，才能揭示原信号真正的物理意义。

2 不同信噪比情况下的算法比较

2．1 混沌系统

本文选择Lorenz混沌系统进行仿真实验。Lorenz系统是一个三维连续动力学系统，其非线性状态方程表达式为：

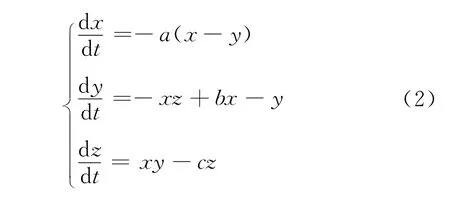
式中参数取a＝10，b＝28，c＝8／3；初始值x0＝y0＝z0＝0．1，步长为0．01，迭代产生4 000点，选取x路信号中1 900到4 000点数据作为混沌背景序列。

2．2 噪声水平对提取效果的影响

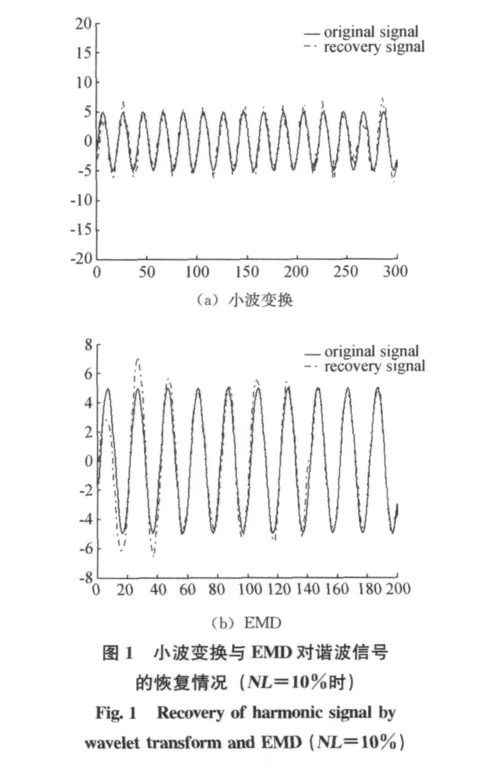
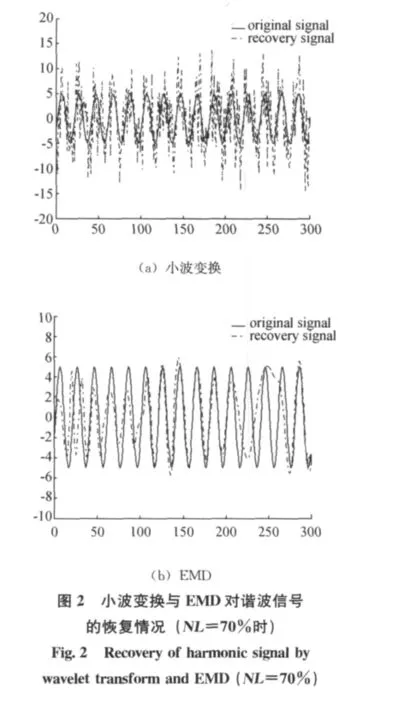
混合信号由混沌干扰信号 （Lorenz混沌系统）、高斯白噪声与谐波信号s（n）＝Asin（2πfn）组成，并采用线性瞬时混合方式。固定A＝5，f＝5Hz，噪声水平NL定义为高斯白噪声与混沌的标准差的比值。改变NL观察小波变换和EMD对谐波信号的分离效果，图1和图2分别给出NL＝10%和70%时，两种方法的分离效果。

由图1和图2可知，当混沌背景中含有一定的白噪声且NL较小时，两种方法的提取效果都比较理想。当NL很大时，小波变换方法的提取波形几乎失真，无法提取谐波信号，而EMD方法仍然适用，效果比较理想。比如，图2中当NL＝70%时小波变换方法恢复出的谐波信号相关系数为0．527 1，EMD方法恢复出的谐波信号相关系数为0．728 6，能够看出其提取效果获得了较大的提高。

令NL分别为 10%，30%，50%，70%，100%，利用小波变换和EMD方法对含噪声的混沌背景中进行信号提取，表1定量给出了分离效果。其中R－wavelet表示运用小波变换方法时，恢复的谐波信号与原信号的相关系数，R－EMD表示运用EMD方法时，恢复的谐波信号与原信号的相关系数。

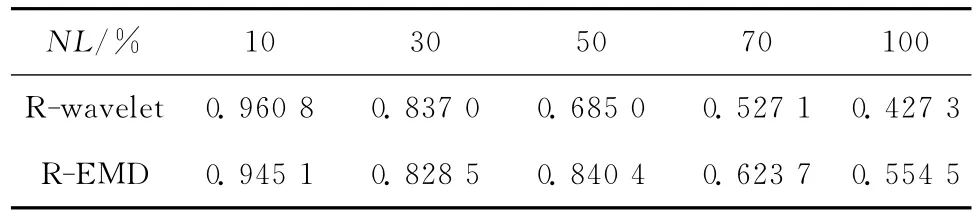
表1 不同NL情况下谐波信号提取效果的比较Table 1 Extraction effect comparison in different NL

由表1可见：当NL＜30%时，用小波变换提取效果比较理想，当NL＞50%时，EMD方法比小波变换方法的提取效果更理想。

2．3 信噪比对提取效果的影响

混合信号由混沌干扰信号 （Lorenz混沌系统）、高斯白噪声与谐波信号s（n）＝Asin（2πfn）组成，其中固定A＝5，f＝5Hz。在NL对提取效果影响的分析结果基础上，固定NL＝30%进行分析。定义信噪比SNR为谐波信号的能量与混沌干扰、高斯白噪声的能量之和的比值。通过改变谐波信号幅值A来改变SNR，对比观察小波变换和EMD方法对谐波信号的分离效果。

取SNR分别为－1，－5，－10，－20，－30，利用小波变换和EMD方法对含噪声的混沌背景中进行信号提取，表2给出相关系数的定量比较。

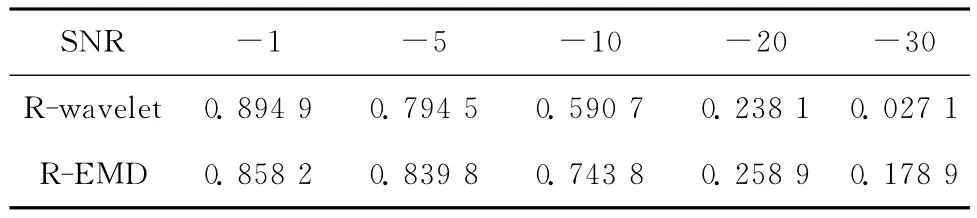
表2 不同SNR情况下谐波信号提取效果的比较Table 2 Extraction effect comparison in different SNR

由表2可见：对于NL＝30%的情形，SNR＞－5时，小波变换优于EMD方法，说明此时小波变换的分解稳定性起着主导作用；当SNR＜－5或更低时，EMD方法更为理想，说明在信噪比较低时，可以直接使用EMD方法对混沌背景中的谐波信号进行提取。

2．4 两种时频方法比较

从以上仿真实验可以得出如下结论：

1）小波变换方法的性能比较稳定，而EMD方法的稳定性较差。这是由于小波分解是一次性完成所有的谐波分解，而EMD是逐个分量递推的过程，前一分量若产生虚假谐波便很快会被逐级放大。

2）对于噪声水平 （NL）较大的混合信号，EMD方法比小波变换更理想。

3）对于信噪比较低的情况，EMD方法比小波变换具有更高的准确度。

表3从参数设置、收敛速度、稳定性和适用信噪比几个方面将小波变换和EMD方法作以比较。

结合前面的仿真结果可以看出，Wavelet和EMD在各方面具有优势互补的特性，可以针对的噪声水平和信噪比情况，在小波变换和EMD方法之间进行切换，选择更好的方法对混沌背景中的谐波信号进行提取。

表3 WT和EMD的消噪性能对比表Table 3 Denosing performance of WT and EMD

3 一种新的谐波信号提取的综合方法

小波变换和EMD方法在噪声水平和信噪比方面具有互补特性，加上两种方法在消噪速度和稳定性上同样具有可以利用的特性，下面将通过仿真实验设计一种将小波变换、阈值去噪与EMD方法相结合的优势互补综合方法。

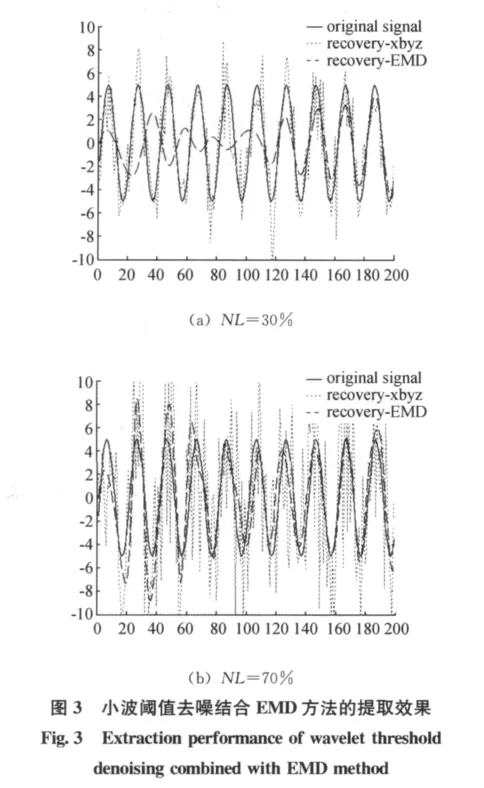
实验1：混合信号由混沌干扰信号 （Lorenz混沌系统），高斯白噪声与谐波信号s（n）＝Asin（2πfn）组成，其中固定A＝5，f＝5Hz。对混合信号先利用小波变换再经过EMD方法进行提取，观测其效果。图3分别给出NL＝30%，70%时的分离效果。“original signal”是原谐波信号，“recovery－xbyz”是经小波阈值去噪后的提取信号，“recovery－EMD”是经EMD方法后的恢复信号。表4给出不同NL情况下，混合方法经每步分离后的相关系数。

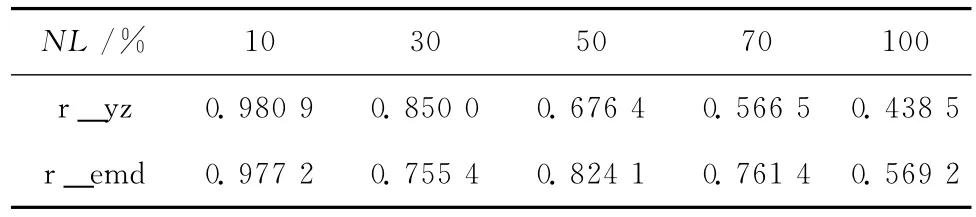
表4 不同NL情况下，小波阈值去噪结合EMD方法提取信号的相关系数Table 4 Correlation coefficients of wavelet threshold denoising combined with EMD in different NL

由图3可知，小波阈值去噪结合EMD的方法当混沌背景中含有的噪声水平NL较小 （如NL＜30%）时，经小波阈值去噪后的信号效果已经很理想，再经过EMD方法后，从相关系数的变化可以看出提取效果反而恶化。这种级联方式增加了算法复杂度却又降低了效果，方法不可取。当噪声水平很大 （NL＞50%）时，小波方法提取波形几乎失真，无法提取谐波信号，再经EMD方法之后提取效果有所提高，比较理想。

实验2：混合信号由混沌干扰信号 （Lorenz混沌系统），高斯白噪声与谐波信号s（n）＝Asin（2πfn）组成，其中固定A＝5，f＝5Hz。对混合信号先经过EMD方法，再经过小波阈值重构方法，观测其分离效果。图4给出NL＝30%，70%时的分离效果，表5给出不同NL情况下，混合方法经每步分离后的相关系数。

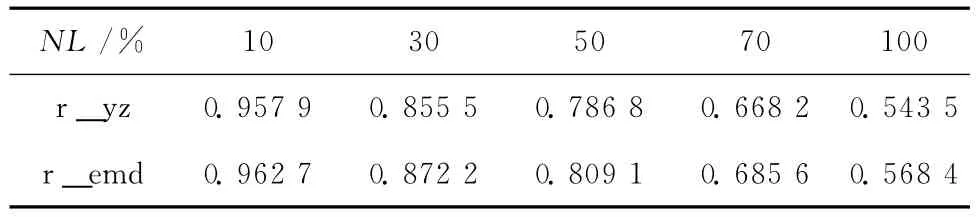
表5 不同NL情况下，EMD结合小波阈值去噪方法提取信号的相关系数Table 5 Correlation coefficients of EMD combined with wavelet threshold denoising in different NL

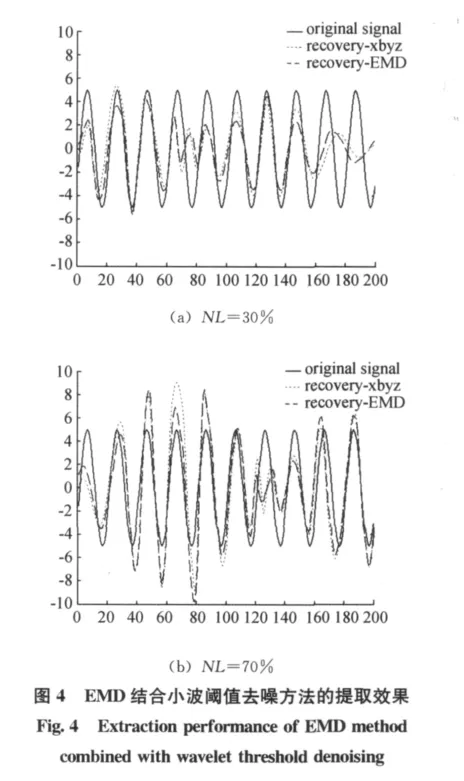
由图4和表5可见，先使用EMD方法，再用小波阈值重构，在不同噪声水平下的混沌背景中信号提取的效果均有提高。这是因为EMD有收敛速度快的优势，将EMD作为第一步消噪方法，可以提高信号的信噪比，为小波变换的后续运用提供了恰当的条件。再利用小波变换稳定性好、精度高的特点进行第二步消噪，进一步提高谐波信号的提取性能。

对比以上仿真实验，可以发现实验2中将EMD方法与小波重构阈值去噪优势互补的综合方法更优。由图3和图4也可看出，同样噪声水平下，后者信号提取效果更为理想。提出一种基于EMD和Wavelet的融合提取方案，方案步骤为：

1）对原混合信号的信噪比水平进行估计，在噪声范围内选择合适的参数、级数。

2）利用EMD可以工作在较低信噪比下以及其收敛速度快的优势，对混合信号进行EMD消噪得到各个IMF分量，初步提取谐波信号分量，观测此时恢复信号的相关系数。

3）利用小波变换稳定性好、精度高的特点进行第二步消噪，经heursure阈值方式进一步降低噪声。

4）以两步消噪后的信号作为提取出的谐波信号。

4 结 论

本文首先介绍时频方法基础理论，然后针对不同噪声水平、SNR情况下的混沌背景中谐波信号的提取性能进行分析，将小波变换与EMD方法进行比较，找出二者比较适用的情况和其优势。经过仿真实验总结出一种新的谐波信号提取的融合方案，并给出融合方案的提取步骤。

［1］MATTHEW B K，HENRY D I，ABARBANEL．False neighbors and false strands：A reliable minimum embedding dimension algotithm ［J］．Physica Review，2002，66 （2）：128－131．

［2］孙晓东，石要武，于晓辉．混沌干扰背景下的正弦频率估计新方法 ［J］．吉林大学学报：工学版，2009，39（5）：1 353－1 357．

［3］李小玲，袁继敏，银 星，等．混沌背景下微弱信号时域参数检测的研究 ［J］．电子科技大学学报，2009，38（4）：569－572．

［4］PACKARD N H，FARMER J D．Geometry from a time series ［J］．Phys Rev Lett，1980，45 （6）：712－716．

［5］CASDAGLI M，Eubank S，FARMER J D．State space reconstruction in the presence of noise ［J］．Physica D，1991，51（1）：52－58．

［6］禹思敏，丘水生．一种语音混沌保密通信方案的研究与硬件实现 ［J］．通信学报，2002，23 （8）：105－112．

［7］H．Leung，X．P．Huang．Parameter estimation in chaotic noise ［J］．IEEE Trans Sig Proc，2006，44：24－56．

［8］汪芙平，郭静波，王赞基，等．强混沌干扰中的谐波信号提取 ［J］．物理学报，2009，50 （6）：1 019－1 023．

［9］BROOMHEAD D S，HUKE J P，POTTS M A S．Cancelling deterministic noise by constructing nonlinear inverses to linear filters［J］．Physica D，2009，89：439－441．

［10］ CAWLEY ROBERT． Local－geometric－projection method for noise ruduction in chaotic maps and flows［J］．Physical review A．2009，46：30－57．

［11］HUANG N E ．The empirical mode decomposition and the Hilbert spectrum for nonlinear and non—stationary time series analysis ［J］．Proc of the Royal Society of London．1998，A （454）：903－995．

［12］D．S．Broomhead，J．P．Huke，M．A．S．Potts．Cancelling deterministic noise by constructing nonlinear inverses to linear filters ［J］．Physica D．2009，89：439－443．

［13］Robert Cawley．Local－geometric－projection method for noise ruduction in chaotic maps and flows ［J］．Physical review A．2009，46：30－57．

［14］Fuping Wang，Jingbo Guo，Zanji Wang，et al．Harmonic signal extraction of strong chaotic interference［J］．Acta Physica Sinica，2009，50 （6）：1 019－1 023．

［15］Xiaodong Sun，Yaowu Shi，Xiaohui Yu．A novel method of sine frequency estimation in chaotic interference ［J］．Journal of Jilin University （Engineering Science）．2009，39 （5）：1 353－1 357．