逐日参考作物蒸发蒸腾量预测的偏最小二乘回归模型

王士兰，王 斌

（1．黑龙江农垦勘测设计研究院，哈尔滨 150030；2．东北农业大学 水利与建筑学院，哈尔滨 150030）

FAO－56推荐的Penman－Monteith公式 （以下简称P－M公式）计算参考作物蒸发蒸腾量 （ET0）的精度较高，被公认为计算ET0的标准方法［1］。然而，P－M公式需要的气象数据较多，虽然这些数据均为常规气象资料，但我国气象观测资料的实时共享程度并不高，在气象数据不完备时无法直接应用P－M公式；即使在气象数据完备情况下，也只能应用P－M公式计算ET0而不能直接预测ET0，除非公式中涉及的各种气象数据均为预测（报）值，但实际工作中很难同时获得如此众多气象数据的预测 （报）值。

国内外关于ET0的预测模型较多，比较典型的有：Tracy等［2］和 Marino等［3］各自提出的基于时间序列分析的ET0预测模型；罗玉峰等［4］提出了ET0预测的傅立叶级数模型；茆智等［5］提出了预测逐日ET0的方法和指数模型；郭宗楼等［6］提出了ET0灰色预测模型；顾世祥等［7］、霍再林等［8］、崔远来等［9］、徐俊增等［10］、彭世彰等［11］应用神经网络对ET0进行了预测；段春青等［12］建立了基于混沌遗传程序设计的ET0预测模型。由于ET0的日变化较剧烈，时间序列分析模型在预测日步长ET0时精度不是很高，而灰色、神经网络方法缺乏机理。本文引入偏最小二乘回归 （Partial Least－Squares Regression，PLS）算法［13］， 分 析P－M公式计算ET0时涉及的部分计算变量的推求过程，应用与天气预报对应的几种常规气象指标观测数据，建立逐日ET0预测模型，以期为预测气象站点可控范围内的ET0提供一种新方法。

1 建模准备

1．1 ET0计算变量分析

FAO－56推荐计算ET0的P－M 公式为［1］：

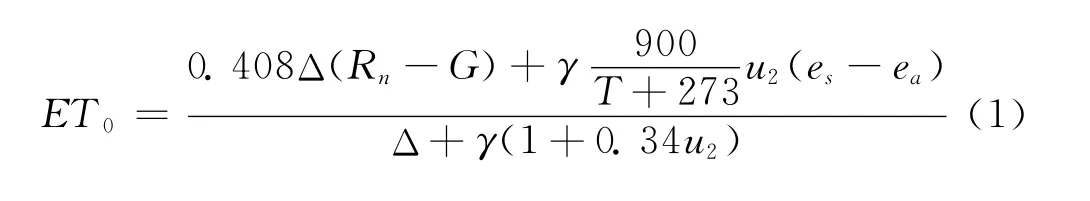
式中ET0为参考作物蒸发蒸腾量，mm／d；T为2 m高处日平均气温，℃；Δ为温度－饱和水汽压关系曲线在T处的斜率，kPa／℃；Rn为作物表面净辐射，MJ·m－2·d－1；G为土壤热通量，MJ·m－2·d－1；γ为湿度表常数，kPa／℃；u2为2m高处风速，m／s；es为饱和水汽压，kPa；ea为实际水汽压，kPa。

从P－M公式计算ET0的具体过程可以看出：

1）一些中间变量 （如：日序数J、日倾角δ、日地相对距离的倒数dr）可以应用公式直接计算；

2）在计算地点 （即纬度）确定后，另外部分中间变量 （如：大气边缘太阳辐射Ra、日照时数角Ws、最大可能日照时数N等）也可以应用公式计算；

3）P－M公式的8项基本计算变量 （T、es、Δ、γ、G、ea、Rn、u2）中有6项 （T、es、Δ、γ、G、ea）与温度有关。因此，对于固定地点，可以考虑选取ET0的部分计算变量构建预测ET0的回归模型［14］。

1．2 天气预报提供的气象信息及其换算

目前，我国天气预报业务比较成熟，在时间上可以向前预报1d或＞1d，在空间上可以预报到县 （市）级甚至乡 （镇）级。每日的天气预报项目一般包括天气状况、日最高气温、日最低气温、风力等级等，这些信息可以很方便地通过各种媒体获得。天气状况与天气指标对应情况见表1，风力等级与风速对应情况见表2。

表1 天气状况与天气指标对应表［15］Table 1 Weather conditions and weather indiators corresponding table［15］

表2 风力等级与风速对应表［16］Table 2 Wind level wind speed corresponding table［16］

为了利用实测的气象数据建模，需使不同天气状况下的n／N以及不同风力等级下的风速变化区间连续，因此分别调整了n／N及风速的变化范围，根据表1换算出了与天气状况对应的αm，见表3；根据表2换算出了与风力等级对应的风速um，见表4。这样处理后，当n／N和风速落入某区间时，建模应用的实际日照时数和风速分别取该区间的nm及um值：

式中N为最大可能日照时数，可应用日序数和当地纬度预先计算，h；αm为修正系数，可根据n／N参考表3取值。

表3 天气状况与αm值对应表Table 3 Weather conditions andαmvalue corresponding table

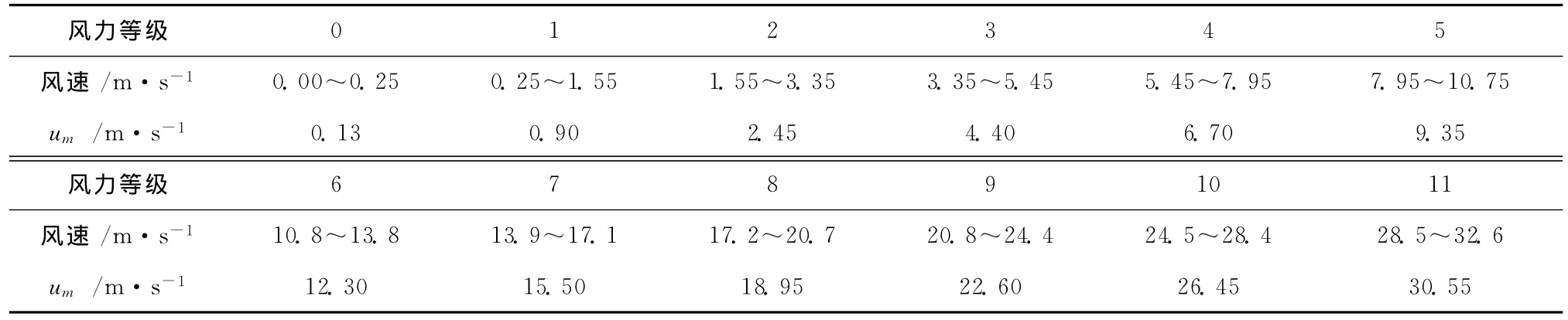
表4 风力等级与um值对应表Table 4 Wind level with the umvalue corresponding table

1．3 选择建模变量

选定Ra、日最低气温Tmin、日最高气温Tmax、T、Tmin时饱和水汽压es（Tmin）、Tmax时饱和水汽压es（Tmax）、饱和水汽压es、Δ、nm和um为建模自变量，P－M公式计算的日ET0为建模因变量。选用这些自变量的原因如下［14］：

1）除nm、um外，其它自变量均为P－M公式计算ET0时的变量；

2）Ra可以直接计算，它不仅综合了计算ET0过程中的J、δ、dr、当地的Ws和N 等信息，还兼顾了Rn的部分计算因子；

3）选取 Tmin、Tmax可以计算es（Tmin）、es（Tmax）、es，通过Tmin和Tmax还可以计算出T、Δ；

4）在应用建成的模型时，不能预知的Tmin、Tmax、nm、um可根据天气预报情况确定，例如：某日的天气预报为 “多云，风力3级，温度10～15℃”，则Tmin＝10℃，Tmax＝15℃，根据表3有nm＝ （0．55 N）h，根据表4得um＝4．40m／s。

综上，所有的建模自变量均可预先计算或根据天气预报确定，当应用前期的气象实测数据率定模型参数以后，就可以根据天气预报情况预测逐日的ET0。

2 偏最小二乘回归方法在逐日ET0预测中的应用

2．1 建模自变量间的相关性分析

应用黑龙江省建三江气象台2001～2006年逐日气象资料，分析了部分自变量之间的相关系数（表5），可见各自变量间的相关系数均较高，这一分析结果对于6a是一致的。此时，常规多元回归分析方法已不再适用。PLS方法采用信息综合与筛选技术，它在变量系统中提取若干对系统具有最佳解释能力的新综合变量 （成分），利用这些新提取的成分进行回归建模。因此，PLS具有普通最小二乘回归方法所不能比拟的优点，恰能较好地解决建模自变量间相关性较高的问题。

2．2 基于PLS的逐日ET0预测模型的建立

黑龙江省大田作物主要生长季为5～9月，其它时段的ET0可计算但对大田农业生产意义不大，因此选取涵盖主要作物生育期的4～10月为研究时段，应用建三江气象台2001～2006年逐日气象资料，采用P－M公式计算了逐年日ET0序列。根据PLS的建模步骤［13］，采用Matlab语言编制了PLS算法程序，应用2001年数据建立ET0预测模型。由于收集不到2001年的天气预报数据，nm和um利用实测的实际日照时数和风速数据，并根据表3和表4中划定的范围转化为对应的数值。经检验提取7个成分已经足够，最后所得原始变量的逐日ET0预测PLS模型为：

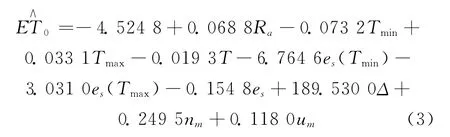
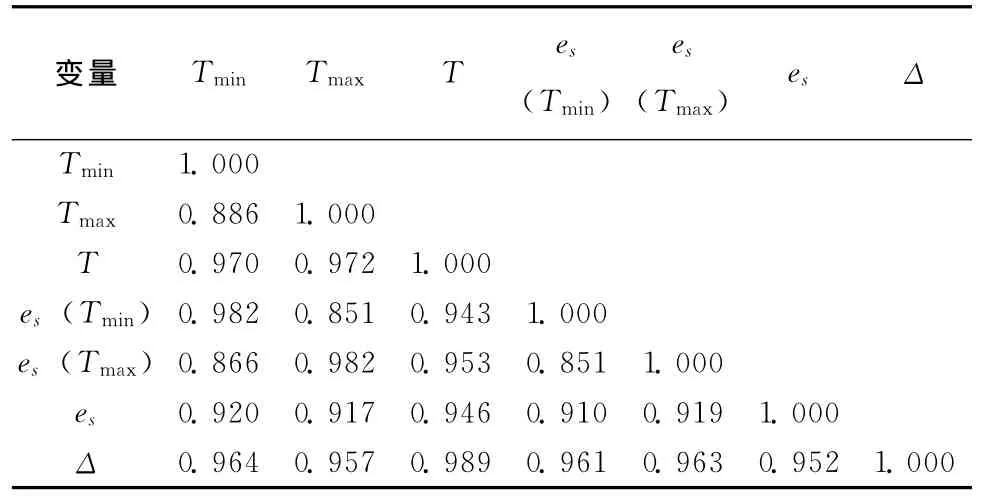
表5 自变量之间的相关系数 （2001年4～10月）Table 5 Between the independent variables，the correlation coefficient（April 2001to October）

2．3 模型拟合及预测效果检验

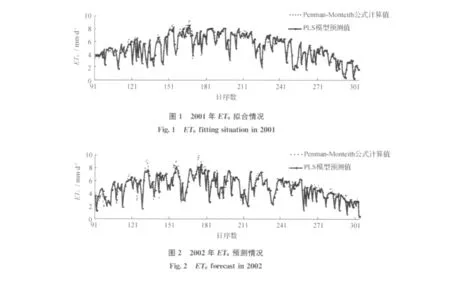
将2001～2006年的建模自变量数据输入建立的PLS模型，应用2001年日样本资料检验模型的拟合效果，应用2002～2006年日样本资料检验模型的预测效果。模型拟合及预测值的合格率见表6，模型输出的ET0值与P－M公式计算的ET0值对比见图1、图2（限于篇幅，仅给出2001年的拟合及2002年预测情况）。

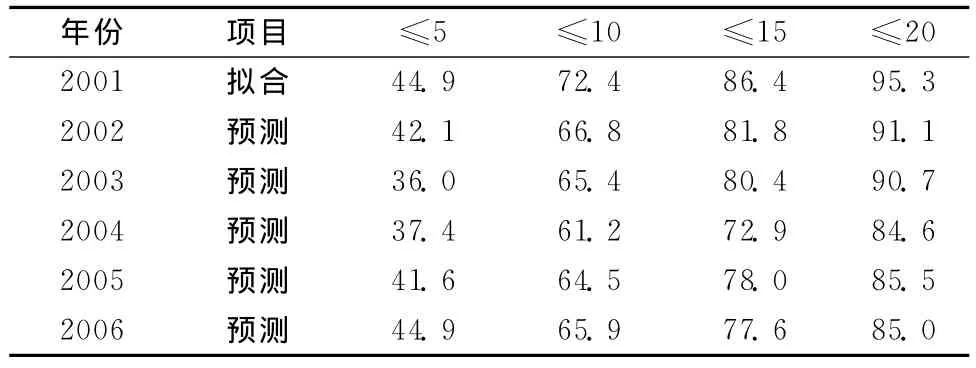
表6 PLS模型拟合及预测值相对误差合格率Table 6 PLS model fit and predictive value relative error qualified rate ／%

由图1、图2及表6可见：PLS模型拟合及预测逐日ET0序列的合格率均较高，从预测平均结果看，逐日ET0预测相对误差的绝对值＜5%、10%、15%、20% 的合格率分别占40．4%、64．8%、78．1%、87．4%。

3 结论与讨论

基于P－M方法计算ET0的过程，分析了该方法涉及的各种计算因子的推求规律，结合天气预报信息，在尽可能多地利用可以直接计算的变量情况下，引入PLS方法，建立了预测逐日ET0的PLS模型。主要结论如下：

1）PLS模型程序编制简单，容易实现，建立的模型参数固定，应用方便，模拟和预测精度较高，基本能够满足农业生产实践的需要。

2）PLS模型需要的Tmin、Tmax、nm和um4项基本气象资料可以根据天气预报数据确定，模型的其它自变量可以直接计算，因此，结合天气预报的日最高气温、日最低气温、天气状况、风力等级等信息，可以应用本文建立的PLS模型预测逐日的ET0。

3）由于收集不到长系列的天气预报数据，PLS模型是在北方寒区单站点条件下应用气象观测数据构建的，研究结论有待进一步检验，但该模型及其建模思路具有一定的实用价值和借鉴意义。

［1］Richard G Allen，Luis S Pereira，Dirk Raes，et al．Crop evapotranspiration－guidelines for computing crop water equirements ［M］．Rome：FAO Irrigation and drainage paper 56，1998．

［2］Tracy J C，Marino M A，Taghavi S A．Predicting water demand in agricultural regions using time series forecasts of reference crop evapotranspiration ［A］．Karamouz M．Water Resources Planning and Management，Saving a Threatened Resource－In Search of Solutions［C］．New York：American Society of Civil Engineers，1992．

［3］Marino M A，Tracy J C，Taghavi S A．Forecasting of reference crop evapotranspiration ［J］．Agricultural Water Management，1993，24：163－187．

［4］罗玉峰，崔远来，蔡学良．参考作物腾发量预报的傅立叶级数模型 ［J］．武汉大学学报：工学版，2005，38 （6）：45－47，52．

［5］茆 智，李远华，李会昌．逐日作物需水量预测数学模型研究 ［J］．武汉水利电力大学学报，1995，28（3）：253－259．

［6］郭宗楼，白宪台，马学强．作物需水量灰色预测模型［J］．水电能源科学，1995，13 （3）：186－192．

［7］顾世祥，李远华，袁宏源．霍泉灌区作物需水量实时预报 ［J］．武汉水利电力大学学报，1998，31（1）：37－41．

［8］霍再林，史海滨，陈亚新，等．参考作物潜在蒸散量的人工神经网络模型研究 ［J］．农业工程学报，2004，20 （1）：40－43．

［9］崔远来，马承新，沈细中，等．基于进化神经网络的参考作物腾发量预测 ［J］．水科学进展，2005，16（1）：76－80．

［10］徐俊增，彭世彰，张瑞美，等．基于气象预报的参考作物蒸发蒸腾量的神经网络预测模型 ［J］．水利学报，2006，37 （3）：376－379．

［11］彭世彰，魏 征，徐俊增，等．参考作物腾发量主成分神经网络预测模型 ［J］．农业工程学报，2009，24（9）：161－164．

［12］段春青，邱 林，黄 强，等．基于混沌遗传程序设计的参考作物腾发量预测模型 ［J］．水利学报，2006，37 （4）：499－503．

［13］王惠文，吴载斌，孟 洁．偏最小二乘回归的线性与非线性方法 ［M］．北京：国防工业出版社，2006．

［14］王 斌，王贵作，黄金柏，等．农业旱情评估模型及其应用 ［M］．北京：中国水利水电出版社，2011．

［15］熊运章，宋松柏，胡彦华，等．计算机在农业水土工程中的应用 ［M］．北京：清华大学出版社，1999．

［16］中国气象局．地面气象观测规范 ［M］．北京：气象出版社，2003．