耦合马尔科夫链和伽马分布函数的降水模拟模型及其应用

付 强，王 斌

（东北农业大学 水利与建筑学院，哈尔滨 150030）

由于降水现象具有随机性特点，在水文水利计算等科研实践工作中，一般应用数理统计方法研究降水现象，应用这类方法的前提是降水资料的样本系列较长。然而，我国大部分地区难以收集到长系列的降水数据，其资料系列一般只有几十年，且多以逐日数据为主。近些年来，各国学者均对降水的模型化和模拟化产生了浓厚的兴趣，很通用的一种方法是采用马尔科夫链和某种分布函数相结合的模型模拟逐日的降水过程，即用马尔科夫链描述降水日的发生，再用选定的某种分布函数产生降水日的降水量［1－4］。本文应用哈尔滨降水资料验证这种延展降水系列的方法，以期为评估我国高寒区降水对农业的影响、旱作区雨水的高效利用、制定合理的灌溉制度等方面提供科学依据。

1 逐日降水的随机模拟模型

1．1 马尔科夫链的两状态转移概率

大量研究表明，在一定的环境条件下，用一阶马尔科夫链描述降水的发生是简单有效的，这种模型不仅能够保持降水的很多重要特性，并且适用性也很好［5－8］。一阶马尔科夫链的两状态分别是降水日 （wet day）和非降水日 （dry day），状态的转换可以用两个转移概率来描述，即由降水日到降水日的转移概率P （W／W）和由非降水日到降水日的转移概率P （W／D）。Shu Geng等对7个站点降水数据进行了统计分析，结果表明，在每个站点，各月份P （W／D）、P （W／W）均与同月降水日出现的频率f间存在线性关系，尤其P （W／D）与f之间具有很强的相关性，可用下式表示［2］：

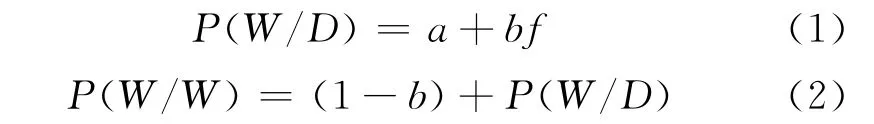
式中f为某月降水日出现频率的多年平均值，可根据实测降水资料推求；a、b为回归系数。

Shu Geng等发现利用式 （1）可以解释各站点不同时间转移概率总变异的96．5%，因此建议采用式 （3）、式 （4）推求转移概率［2］：

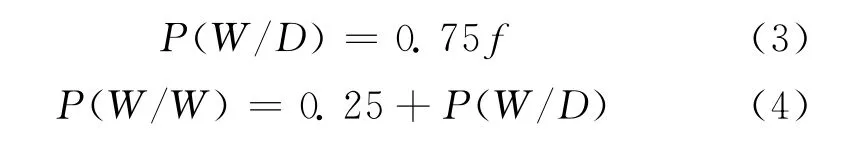
1．2 伽玛分布及其参数

如果连续型随机变量X的密度函数为式 （5），则称X服从伽玛 （Gamma）分布：

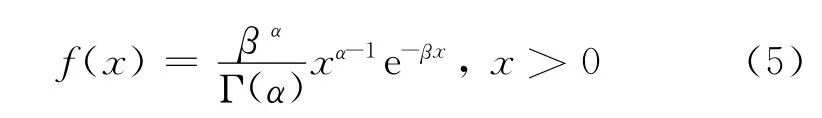
式中α为伽玛分布的形状参数；β为伽玛分布的尺度参数。

设X为表示日降水量的随机变量，当X服从伽玛分布时，根据伽玛分布函数的统计特性，参数α和β也可根据实测降水资料求得。Shu Geng等在分析各站点降水数据时还发现，参数β与多年平均各月降水日的降水量之间也存在很强的线性关系，应用7个站点的平均结果得到了式 （6）、式 （7），在不同地区和不同的月份间，利用该式也可以解释96．5%总变异［2］：

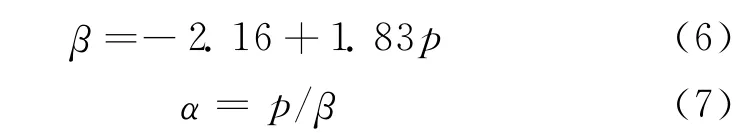
式中p为某月降水日降水量的多年平均值。

1．3 逐日降水序列的产生

当转移概率和伽玛分布参数确定以后，利用计算机产生 ［0，1］区间上均匀分布的随机数，并将这个随机数与P （W／D）和P （W／W）相比较，估计该日是否产生降水。对降水日降水量的模拟就是求出指定P所对应的随机变量X的取值xP，即求出的xP应满足F （X＞xP）＝P，亦即：

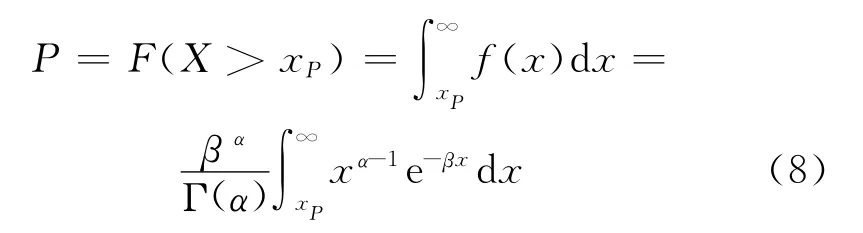
当为降水日时，利用式 （8）通过数值积分即可求得降水日的降水量。

2 模型应用实例

利用f和p估计转移概率和伽玛分布参数，不仅简化了逐日降水模拟模型，而且扩大了该模型的适用范围。本文应用哈尔滨1961～2008年的逐日降水数据，检验该方法在我国高寒地区应用的有效性。由于直接积分式 （8）非常繁杂，因此应用Matlab软件的伽玛分布函数 （GAMRND）实现式（8）的计算过程，即将α、β两个参数提供给GAMRND函数，令该函数产生服从伽玛分布的随机数列［3－4］。

2．1 转移概率和伽玛分布参数的确定

应用哈尔滨48a的降水资料，统计出哈尔滨各月的P （W／D）、P （W／W）及f见图1。由图1可见，P （W／D）、P （W／W）与f的月份变化趋势基本一致。统计分析结果表明，哈尔滨的P（W／D）、P （W／W）与f之间均存在很强的相关性，且P （W／D）与f之间的相关性更强，这与文献 ［2］的研究结论相同，P （W／D）、P （W／W）与f的回归方程见式 （9）、式 （10）：

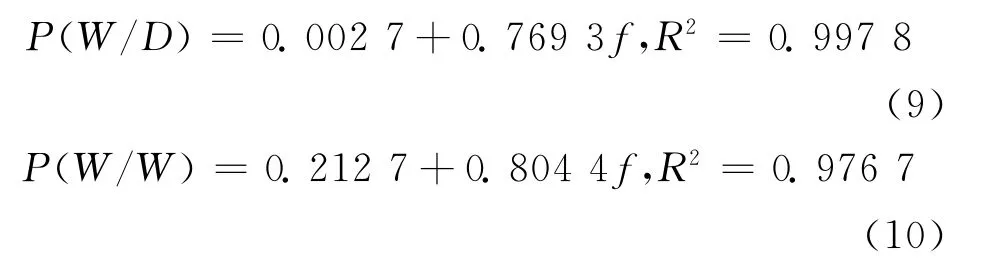
图1 哈尔滨降水的转移概率和降水日发生频率Fig．1 Precipitation transition probability and occurrence frequency per day in Harbin

根据哈尔滨48a实测降水资料，求得哈尔滨12个月份的α、β及p见图2。由图2可见，α与p间的月份变化趋势差别很大，而β与p各月的变化趋势基本一致。统计分析结果表明，哈尔滨的α与p之间的线性关系很差，但β与p之间具有很强的线性关系，这也与文献 ［2］的研究结论相同。β与p的回归方程见式 （11）：

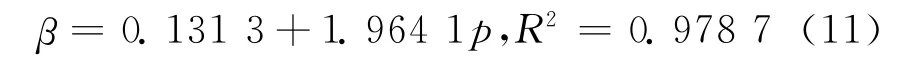
对比式 （9）、式 （10）与式 （3）、式 （4），以及式 （11）与式 （6）可以看出，应用哈尔滨实测降水数据求得的回归模型与文献 ［2］中建议的经验公式存在较大差别，但与文献 ［4］的研究结果相近。因此，即使在外国能适应很大环境变化范围的模型，却不一定适合我国的部分地区。

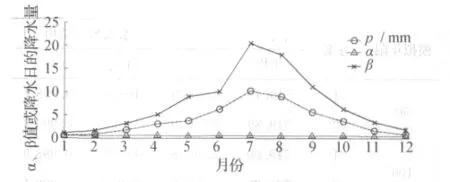
图2 哈尔滨降水的伽玛分布参数和降水日降水量Fig．2 Precipitation Gamma distribution parameters and daily precipitation in Harbin

2．2 逐日降水过程模拟及分析

以50、100、200、500、1 000a为模拟年限 （对于每种年限的模拟，均假设从一个非降水日开始），采取两种方案模拟哈尔滨的逐日降水过程，两种方案依次为：①统计分析实测降水数据直接确定P （W／D）、P （W／W）、α、β；②根据统计实测降水数据得到的f、p，再利用式 （9）、式 （10）、式 （11）、式（7）间接推求出P （W／D）、P （W／W）、α、β。模拟的月份平均结果见表1、表2，精度分析 （各月份的模拟数据与实测数据的相关系数r）见表3。

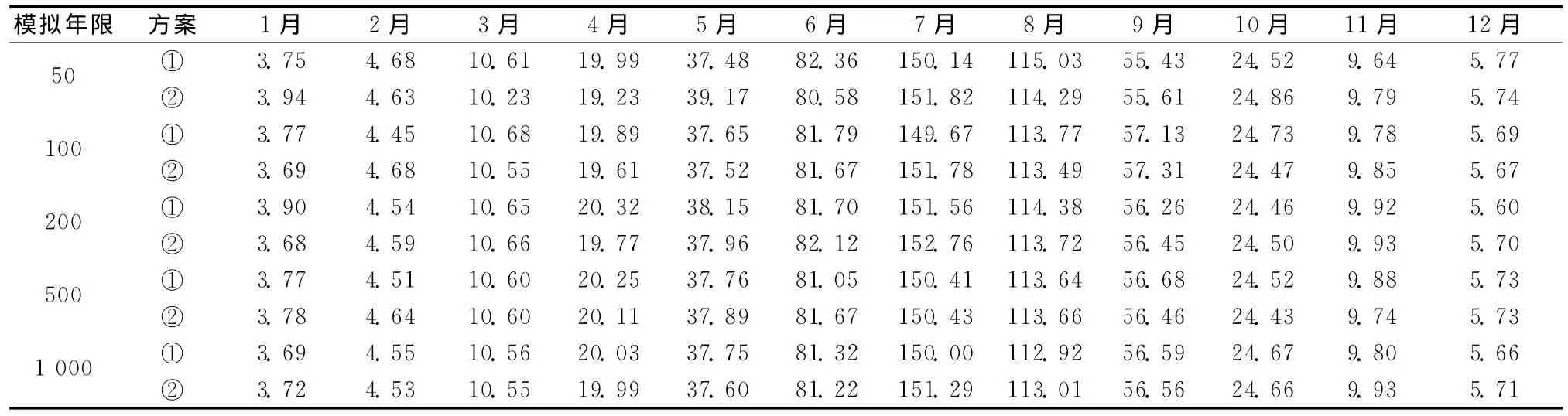
表1 哈尔滨降水量模拟值Table 1 Precipitation simulation values in Harbin ／mm

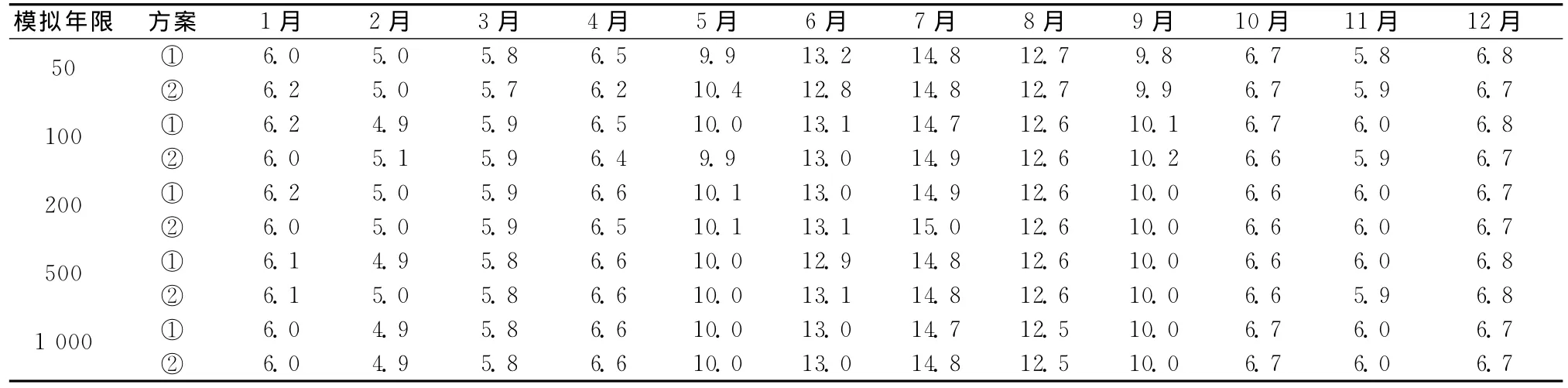
表2 哈尔滨降水天数模拟值Table 2 Simulation value of precipitation day in Harbin ／d

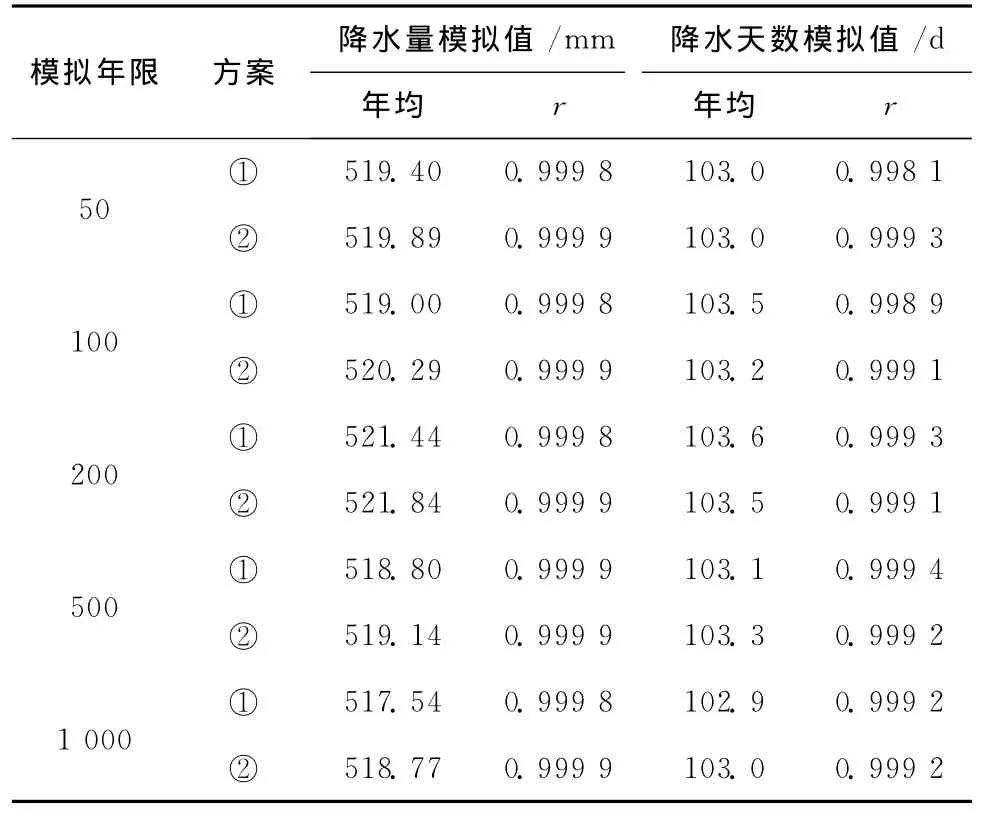
表3 模拟值与观测值的相关系数Table 3 The correlation coefficient between simulation values and observed values

由表1～表3可见：对于不同模拟年限的降水系列，模型模拟的精度很高，不同模拟年限间的模拟结果间并无显著差别。因此，根据实际需要，可以应用上述方法，选择一定的模拟年限模拟哈尔滨的逐日降水过程。对于哈尔滨周边地区，当降水资料不全时，如果能收集到该地区每月降水天数和降水量的多年平均值，即可确定f、p，利用式 （9）、式 （10）、式 （11）、式 （7）等即可模拟该地区的逐日降水过程。

3 结 论

哈尔滨的P （W／D）和P （W／W）与f之间，以及β与p之间均存在很强的线性关系，这与国外的研究结论相同，但建立的回归模型系数与国外地区的经验公式差别较大，因此，在引进国外模型模拟逐日降水过程时，模型及其参数的有效性需要实地数据验证。

利用哈尔滨实测降水资料确定P （W／D）、P（W／W）、α、β后，应用一阶马尔科夫链和伽玛分布函数相结合的随机模型可以模拟哈尔滨的逐日降水过程，模型的模拟精度很高；本文建立的3个回归模型的R2＞0．97，应用此3个模型，也可为资料不全的哈尔滨周边地区模拟逐日降水过程时提供参考。

［1］Stern R．D．，Coe R．The use of rainfall models in agricultural planning ［J］．Agric．Meteorogy，1982，26：35－50．

［2］Shu Geng，Frits W．T．Penning de Vries，Iwan Supit．A simple method for generating daily rainfall data ［J］．Agricultural and Forest Meteorology，1986，36：363－376．

［3］王 斌，付 强，王 敏，等．几种模拟逐日降水的分布函数比较分析 ［J］．数学的实践与认识，2011，41 （9）：128－133．Wang Bin，Fu Qiang，Wang Min，et al．Comparative analysis on three distribution functions simulating daily rainfall ［J］．Mathematics in Practice and Theory，2011，41 （9）：128－133．

［4］王 斌，付 强，张金萍，等．逐日降水的随机模拟模型及其在黑龙江省的应用 ［J］．农机化研究，2011，（9）：65－69．Wang Bin，Fu Qiang，Zhang Jinping，et al．Stochastic model of generating daily rainfall data and its application in Heilongjiang Province ［J］．Journal of Agricultural Mechanization Research，2011，（9）：65－69．

［5］Ahmed J．，Van Bavel，C．H．M．，et al．Optimization of crop irrigation strategy under a stochastic weather regime：a simulation study ［J］．Water Resour．Res．，1976，12：1 241－1 247．

［6］Delleur J．W．，Kavvas M．L．Stochastic models for monthly rainfall forecasting and synthetic generation［J］．J．AppL MeteoroL，1978，17：1 528－1 536．

［7］Nicks A．D．，Harp J．F．Stochastic generation of temperature and solar radiation data ［J］．J．Hydrol．，1980，48：1－17．

［8］Bruhn J．A．，Fry W．E．，Fick G．W．Simulation of daily weather data using theoretical probability distributions［J］．J．Appl．Meteorol．，1980，19：1 029－1 036．