同伦摄动法在弹性力学中的应用

银 山，特木尔朝鲁

（1.内蒙古工业大学 理学院，呼和浩特 010051；2.上海海事大学 文理学院，上海 200135）

同伦摄动法在弹性力学中的应用

银 山1，特木尔朝鲁2

（1.内蒙古工业大学 理学院，呼和浩特 010051；2.上海海事大学 文理学院，上海 200135）

本文中，应用同伦摄动法给出弹性力学的非线性问题,均匀载荷作用下边界可移夹紧的圆薄板问题的新的近似解.并且给出与传统的摄动解之间的对照图,从而说明同伦摄动法在弹性力学的非线性问题中有效性.

薄板；同伦摄动法；卡门方程

1 引言

非线性问题是在弹性力学中热门问题之一.板的大挠度问题是典型的非线性边值问题之一,其控制方程是著名的卡门方程[1].所以很多研究人员研究了卡门方程并且给出了很好的具有实际意义的成果.如韦(S.Way)[2]曾用幂级数解研究了在均布载荷下边缘固定的圆薄板问题；李斐(S.levy)[3]用重三角级数法得到了均布载荷下简支长方板的数值解；钱伟长[4,5]用摄动法重新处理了均布载荷下和各种不同边界条件下的圆薄板的大挠度问题；叶开源[6]利用摄动法处理了边缘载荷下环形薄扳大挠度问题，Q.S.Lia，Jie Liu等人[7]提出了分析大挠度薄板的屈曲的新方法,其他[8-11]等等.

近几十年内，非线性问题的解析法得到了很大的发展，且出现了很多解析法，如Adomain解析法[12]，变分迭代法[13]，同伦摄动法[14,15]等等.但是这些方法在弹性力学领域中很少被应用.

本文中,利用同伦摄动法给出均匀载荷作用下边界可移夹紧的圆薄板问题的新近似解.在[4,5]中作为摄动参数的中心挠度a在本文中分解为级数.这有利于控制近似解得精度.细节在下一节中给出.均匀载荷作用下边界可移夹紧的圆薄板问题的基本方程是著名的卡门方程

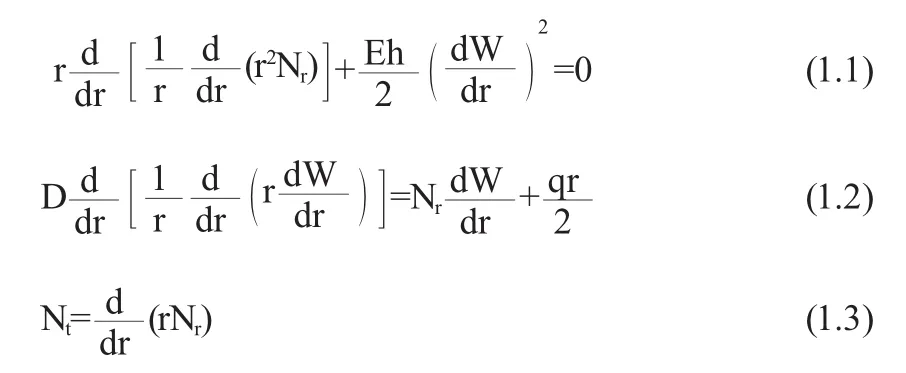
边界条件为

其中W,Nr分别表示挠度和径向正应力；q,h和b分别表示均匀载荷、圆薄板的厚度和半径；μ,E是泊松比和杨氏弹性模量；D=Eh3/(12(1-μ2))是板的抗弯系数.通过下面无量纲化变换

边值问题(1.1)-(1.5)重新写成下列形式

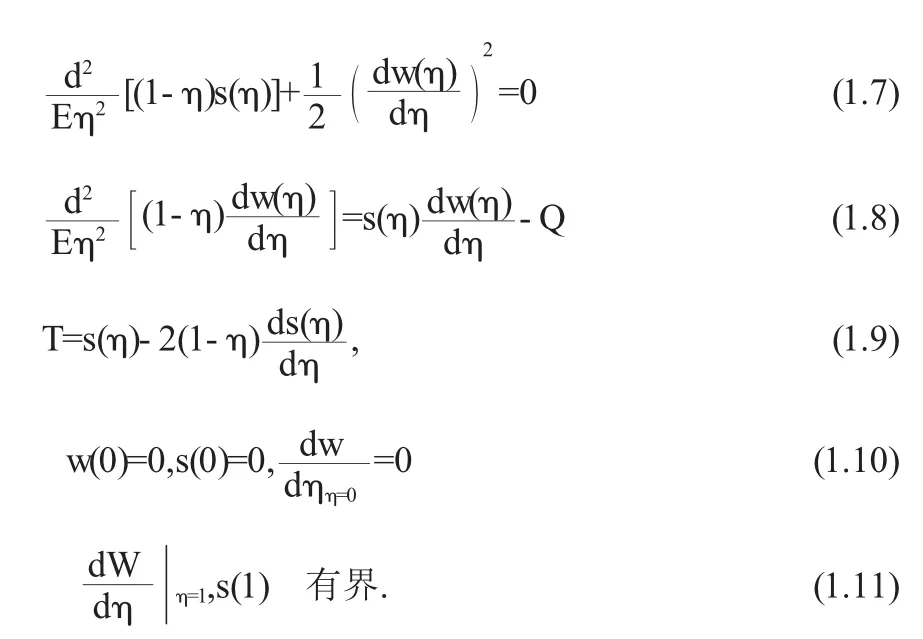
其细节见[4].

2 利用同伦摄动法解该非线性边值问题

通过变换w(x)=au(x),边值问题(1.7)-(1.11)改写为

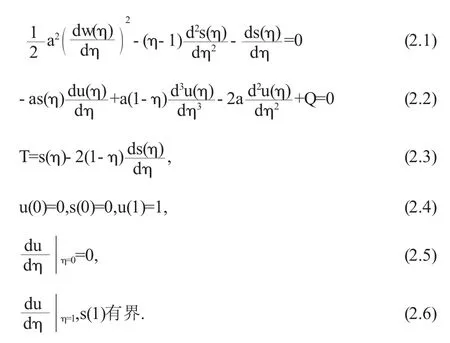
其中w(1)=a.现在，对方程(2.15)构造同伦

现在,把(2.8)-(2.11)代入(2.1)与(2.7),并令 pi(i=0,1,2,…)的系数为零.根据边界条件(2.4)-(2.6),得到下列形式的一些线性边值问题

从(2.12),得到

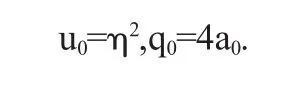
把上式代入(2.13),解得

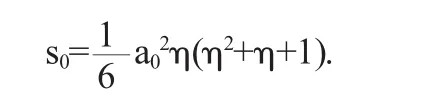
类似的方法，能解出其余的u1,q1,sj(i,j=1,2,…,n)

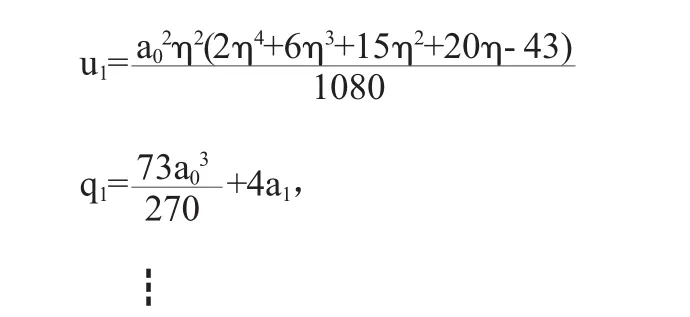
最后，令p=1，得到n阶近似解

3 结论

根据同伦摄动法，由定义如下近似误差

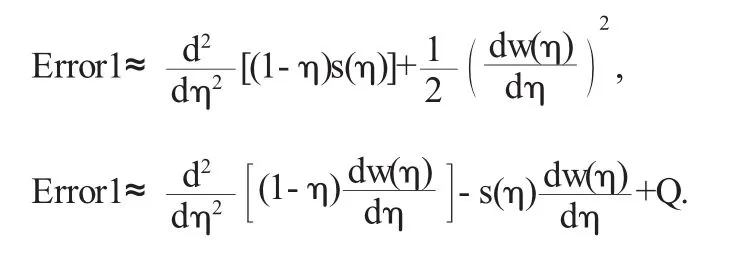
对四阶近似解与四阶摄动解[5]的误差线的对照，其中μ=0.3,a0=0.498,a1=0.0019999,a2=0.0000000999,a3=0.00000000001.由此,证实同伦摄动法在该非线性边值问题中的有效性.对应的四阶近似解曲线如图3-4所示.在传统的摄动法中作为摄动参数的中心挠度[5],根据近似解的阶数，分解为有限级数,即对n阶近似解,a分解为

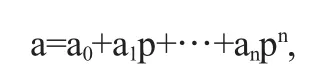
而且a的恰当的分解直接影响近似解的误差.

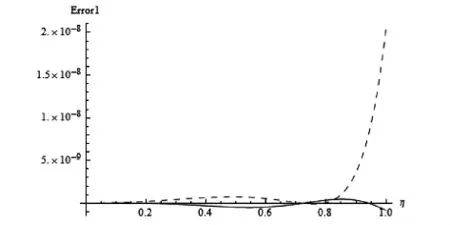
图1 Error1 η曲线

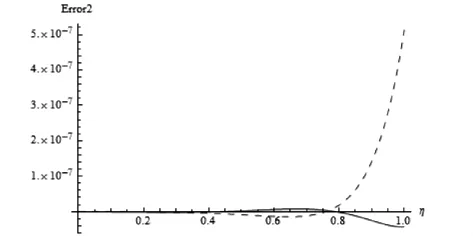
图2 Error2 η曲线

〔1〕Theodore Von Karman. Festigkeits problem in Mashinenbau[J].Enzyklopadie der mathematischen Wissenschaften,1910,4:348-351.

〔2〕S.Way.Bending of Circular Plate with Large Deflections[J].Trans.ASME Applied Mechanics.1934,56:627-636.

〔3〕S.Levy.Bending of rectangular plate with large deflections[z].NACA Report 737,1942.

〔4〕Wei-zang Chien.Large deflection of a circular clamped plate under uniform pressure[J].Acta Physica Sinica,1948,7:102-113.

〔5〕Wei-zang Chien,Yeh Kai-yuan.On the large deflection of a circular thin plate[J].Acta Physica Sinica,1954,10:209-238.

〔6〕叶开源.边缘载荷下环形薄扳大挠度问题[J].物理学报,1953（9）:110-129.

〔7〕Q.S.Li,Jie Liu,H.B.Xiao.A new approach for bending analysis of thin circular plates with large defection[J].International Journal of Mechanical Sciences,2004,46:173-180.

〔8〕黄会荣,郝际平,郭家元.直角坐标下厚圆柱扁壳弯曲的一般解[J].应用力学学报,2011（28）:153-157.

〔9〕刘辉.现浇混凝土空心板弹性挠度计算分析[J].赤峰学院学报（自然科学版）,2011：153-154.

〔10〕Ye Kai-yuan.New development in the investigation of flexible structural elements[J].Advances in mechanics,1987,17:1-10.

〔11〕Liu Ren-huai,Yuan Hong.Overview of theory development for elastic elements at home and abroad[J].Instrument Technique and Sensor,2011,9:1-8.

〔12〕G.Adomian.A review of the decomposition method in applied mathematics[J],J.Math.Anal.Appl.,1988,135:501-544.

〔13〕J.-H.He.Variational iteration method-a kind of non-linear analytical technique:some examples[J],Internat.J.Non-Linear Mech.,1999,34:699-708.

〔14〕J.-H.He.New interpretation of homotopy perturbation method[J].International Journal of Modern Physics B,2006,20:2561-2568.

〔15〕斯琴，斯仁道尔吉.同伦摄动法与KdV-Burgers方程和BBM方程的近似解 [J].赤峰学院学报 （自然科学版）,2008（1）：5-8.

O343.5；O29

A

1673-260X（2012）04-0001-03