基于Newmark－β显式直接积分法的三塔斜拉桥非线性地震响应分析①

喻明秋，祝 兵，张斗龙

（1．攀枝花市规划和建设局，四川攀枝花 617000；2．西南交通大学土木工程学院，四川成都 610031；3．檀慕信息技术（上海）有限公司成都分公司，四川成都 610031）

基于Newmark－β显式直接积分法的三塔斜拉桥非线性地震响应分析①

喻明秋1，祝 兵2，张斗龙3

（1．攀枝花市规划和建设局，四川攀枝花 617000；2．西南交通大学土木工程学院，四川成都 610031；3．檀慕信息技术（上海）有限公司成都分公司，四川成都 610031）

三塔单索面斜拉桥在空间动力行为方面有其独特之处。以济南建邦黄河公路大桥为例，运用有限元方法建立桥梁的空间动力数值分析模型，构建结构特征方程，在频率范围1 600～0cps，频移为1cps基础上运用lanczos法解此方程获得结构空间动力特性；进而利用拟相对速度反应谱SV和拟绝对加速度反应谱SA之间的数学关系，在大量地震记录中选择与场地特征周期基本一致的波谱，对其峰值加速度和持续时间进行调整后直接输入动力数值模型；采用质量和刚度因子法计算结构各振型阻尼比，以恒载作用下结构受力状态作为初始状态，运用Newmark－β显式直接积分法迭代求解结构动力微分方程组，并取γ≥0．5且β≥γ／2以满足其无条件稳定；考虑恒载作用在地震发生过程中对结构产生的二阶效应，获得非线性地震响应数值解，并由此总结出该类桥型的地震响应一般规律。结果可为该类桥型的抗震设计提供参考。

三塔单索面斜拉桥；动力特性；无条件稳定；二阶效应；Newmark－β显式直接积分法

Abstract：Cable－stayed bridge with three towers and single cable plane has uniqueness on dynamic behavior in space．In this paper，the Jianbang Yellow River Highway Bridge in Jinan is taken，as example，using finite element method to build spatial dynamic numerical analysis model of the bridge，and to form a structural characteristic equation，the space dynamic characteristics of the structure is obtained with frequency range of 1 600～0cps and frequency shift 1cps by using lanczos methods for the solution of the equation．The mathematical relationship between pseudo relative velocity response spectrum SVand pseudo absolute acceleration response spectrum SAis used to select the spectra with basically same characteristic site period in a large number of seismic records，whose peak acceleration and duration are adjusted to directly be input to the dynamic numerical analysis model．Using mass and stiffness factor method in calculation on damping ratio of every vibration type，taking stressed state of the structure under dead load as the initial state，Newmark－βexplicit scheme direct integration method withγ≥0．5andβ≥γ／2which make the method being no－conditional stable is used to the solution of the structure dynamic differential equations．Considering the second order effect from dead load in the structure during an earthquake，the numerical solution of nonlinear seismic response is obtained．Furthermore，general laws on seismic response of such bridge type is concluded to provide a feasible basis for seismic design of such bridge type．

Key words：Cable－stayed bridge with three towers and single cable plane；Dynamic characteristics；No－conditional stable；Second order effect；Newmark－βexplicit scheme direct integration method

0 引言

大跨度桥梁结构准确的地震响应计算是其抗震设计的前提和基础，而地震响应计算结果的可信度与计算方法息息相关。1899年至今结构地震响应计算方法经历了静力法—反应谱法—时程法和随机振动法的发展历程［1－2］。静力法由于忽略了结构自身的动力特性，只有当结构基本周期比场地特征周期小很多时才能成立，因此存在很大的局限性［1］；反应谱法尽管在一定程度上考虑了结构的动力特性，但设计反应谱源于强震记录的统计分析，而过去大多使用的模拟式强震仪在长周期部分严重失真［1］，因此对于基本周期较长的大跨度斜拉桥反应谱法的计算结果难以令人信服。上世纪60年代后，随着计算机技术的迅猛发展时程分析法被引入到大跨度桥梁的分析当中。动态时程分析法从选定合适的地震动输入出发，采用多节点多自由度的结构有限元动力计算模型建立地震振动方程，然后采用逐步积分法对方程进行求解，计算地震过程中每一瞬时结构的位移、速度和加速度反应，从而分析出结构在地震作用下弹性和非弹性阶段的内力变化以及构件逐步开裂、损坏直至倒塌的全过程［2］。本文在简要介绍Newmark－β显式非线性直接积分法算法思想的基础上，选择济南建邦黄河公路大桥为研究对象，通过在大量原始地震记录中筛选特征周期和场地特征周期基本一致的地震记录，然后将经过强度和持续时间调整后的地震波直接输入模型，构建结构动力微分方程组，采用质量和刚度因子法计算结构各振型阻尼比，运用Newmark－β直接积分法求解动力微分方程组，并从结构体系的特点出发，分析结果的合理性。

1 Newmark－β显式直接积分法概述

当满足γ≥0．5，β≥γ／2时，Newmark－β显式法具有无条件稳定的优点［3］。采用Newmark－β法求解结构动力微分方程组的具体过程如下［1，3－4］。

单自由度质量系统动力方程的增量形式写为

Newmark－β法中设

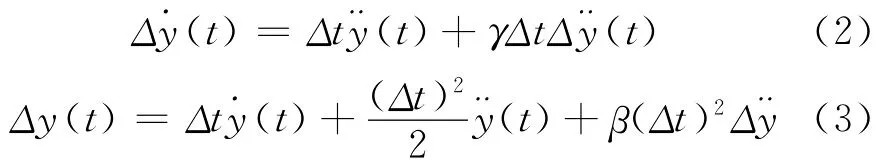
从式（2）、（3）可求出

将（4）、（5）两式代入式（1）得

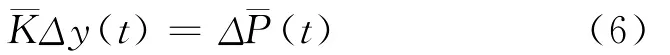
式中

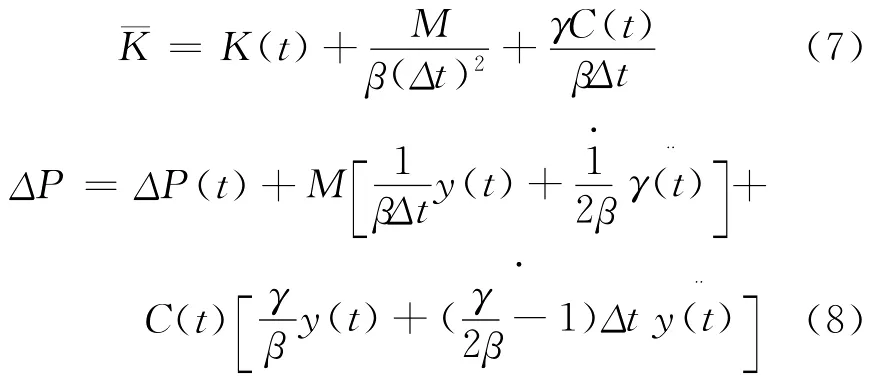
通过式（6）计算出位移增量Δy（t）后就可以由式（5）求出速度增量Δ˙y（t），由此可以得出下一段的起始值：

如此一个时间步长计算完毕。重复以上步骤可以一步一步地计算下去，查到所需时程范围为止。Newmark－β方法中关键是先取β，γ值。其中γ控制人工阻尼，当γ＝0．5时，无人工阻尼；当满足γ≥0．5，β≥0．5γ，Newmark－β法是无条件稳定。通常取γ＝0．5，通过调整β值以期达到对加速度的各种修正。

2 桥梁工程概况

济南建邦黄河公路大桥为三塔单索面斜拉桥，跨度布置为53．5m＋56．5m＋2×300m＋56．5m＋53．5m（图1）。主梁横断面采用单箱四室斜腹板截面，梁高3．5m，顶板宽30．5m，底板宽9m，两侧悬臂长4m。中塔采用塔、梁、墩固结，与塔、墩相交处各设1道横梁，厚7m。中塔下塔柱分为两部分：一是高6．2m、直径16m的圆柱体，二是分开两边高16．25m、半径8m的半园斜柱体，横向宽度为9 m，两部分均为实体结构。中塔上塔柱均采用空心矩形断面，横向宽度均为4m，纵向塔顶宽为8m，竖向经半径为260m的圆弧过渡至主梁顶外侧至外侧宽20m，并在距梁顶22．54m高度处分离为两个宽为4．9～6m的斜腿；上塔柱高86．64m，索锚区基本壁厚为横桥向0．7m，顺桥向1．4m，在分开成斜腿上部一定范围内横向壁厚逐渐加厚，斜腿部分基本壁厚为横桥向1．2m，顺桥向1．4m。边塔下塔柱高18．1m，横桥向等宽9m、顺桥向等宽7 m，采用单箱四室截面，基本壁厚横桥向1．0m，中间隔板2．0m，顺桥向1．0m，中间隔板0．8m；上塔柱横向宽度均为4m，纵向塔顶宽为7m，上塔柱高67．4m，索锚区基本壁厚为横桥向0．7m，顺桥向1．4m。

图1 济南建邦黄河公路大桥立面图（单位：m）Fig．1 Elevation of Jianbang Yellow River Highway Bridge in Jinan（unit：m）．

3 动力数值模型与输入地震波

运用有限元方法建立桥梁的动力数值模型过程中做如下考虑：

（1）数值模型中恒载包括结构自重、预应力和斜拉索成桥索力，以结构在恒载作用下的受力状态作为初始状态，动力微分方程组的求解过程即是以此初始状态为时间零点的迭代过程。由于在迭代过程中引入了结构的恒载，因此计算结果中包含了恒载各分量耦合产生的二阶效应。

（2）在实际地震作用前将恒载效应以单元初始内力的形式输入模型，真实地震续接恒载作用，可以真实反映震前结构内力和应力状态。

（3）模型中桥面部分采用脊梁模式，将原主梁的轴向刚度、弯曲刚度、扭转刚度和剪切刚度均集中到主梁上，可以采用一致刚度和一致质量矩阵来描述。

（4）主梁、塔柱采用空间梁单元进行模拟，单元划分基本与施工节段一致；斜拉索采用桁架单元模拟，用Ernst公式修正弹性模量以考虑垂度效应，一个单元即为一根拉索。

（5）斜拉索锚固点与主梁、主塔的相对位置准确设定，确保斜拉索倾斜角度精确，采用刚性连接的办法连接拉索锚固点与主梁和主塔。

（6）主梁和中塔采用共节点和刚性连接的方式模拟塔梁固结，主梁与边塔连接按照实际的约束关系采用弹簧单元模拟。

（7）横隔板重量、二期恒载和边跨压重是结构重力的组成成分，计算中转换为节点质量考虑。

因缺乏桥址处地震危险性分析资料，本文场地特征周期按Ⅲ类场地取用。根据建筑抗震设计规范［5］的规定，地震分组为第二组，场地特征周期为0．55s。利用拟相对速度反应谱SV和拟绝对加速度反应谱SA之间存在的近似数学关系计算出地震波的圆频率ω，从而获得地震波特征周期，在大量地震记录中选择与在建场地特征周期基本一致的James rd地震波做强度和持续时间调整。通过建筑抗震设计规范［5］可知，济南市抗震设防烈度为Ⅵ度，鉴于该桥的重要性，本文提高一度进行考虑，峰值加速度调整为0．12g，地震持续时间取40s，其中最后2s加速度取为0，以观察地震激励停止后结构的动力反应。调整后的James rd地震波如图2所示。

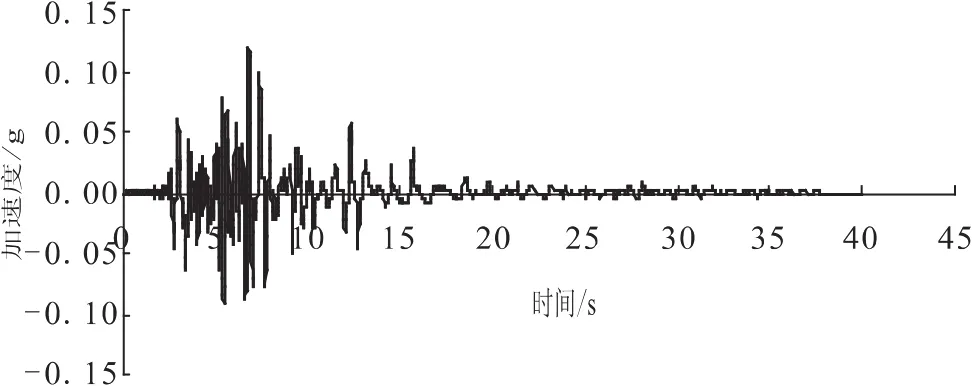
图2 调整后的James rd地震波Fig．2 Adjusted James rd seismic wave．

4 地震响应结果与分析

将调整后的地震波分别沿桥梁纵向、横向、竖向和三向耦合输入，分别计算结构在地震激励下的内力和位移响应，并对结构地震响应规律作出分析总结。限于篇幅，仅列出纵向输入和三向耦合输入计算结果。

4．1 恒载作用

将恒载作用下结构的内力和变形作为后续实际地震作用的初始状态，可以帮助我们把握实际地震激励作用于结构上时地震荷载本身对结构的内力和变形的贡献，同时，恒载作用参与动力微分方程组的迭代过程，可以很好的考虑其二阶效应的影响。恒载作用下典型部位内力值如表1所示。

4．2 纵向地震波单独作用

纵向地震波单独作用下结构典型部位动力响应结果如表2所示，东边塔与中塔纵向移峰值包络图、中塔塔顶纵向位移时程曲线与中塔塔根弯矩时程曲线分别如图3（a）、（b）、（c）、（d）所示。

表1 恒载作用下典型部位内力响应值

表2 James rd地震波纵向作用下典型部位内力响应值

在纵向地震作用下结构主要表现为纵向响应。内力方面主要体现在主梁轴力和中塔塔根纵向弯矩与纵向剪力。其中中塔塔根部位纵向弯矩值和纵向剪力值均非常大，其中弯矩为162 263．50kN·m，剪力为6 566．12kN。笔者认为地震荷载造成结构这一受力特点的原因在于桥梁的两边塔对主梁纵向没有约束而中塔与主梁固结，主梁在纵向地震激励下的强大惯性力大部分通过中塔传递给基础，使得中塔承受了很大的纵向力，这一纵向力在塔根部位形成了巨大的弯曲和剪切作用。设计中必须考虑抗震钢筋的配置并进行承载力验算。位移方面，两边塔纵向最大位移较中塔更大，其中西边塔与东边塔纵向最大位移均为32mm，而中塔纵向最大位移小于两边塔位移，为30mm。笔者认为造成这一变形特点的原因有两点：①中塔侧面采用倒“Y”和“Y”形相结合的结构形式，其纵向刚度远大于边塔；②中塔与主梁固结，而边塔与主梁之间没有纵向约束，因此中塔的悬臂长度应从主梁处算起为168．8m，而边塔的悬臂长度应从塔根部算起为170．2m，说明尽管中塔高度大于边塔，但中塔的悬臂长度却比边塔更小，因此中塔纵向位移较边塔更小。从图3（c）、（d）可以看出，地震波输入初期，中塔塔顶纵向位移时程曲线和中塔塔根纵向弯矩时程曲线的走势与地震波波谱具有一定的相似性，但时程曲线波峰与波谷出现的时间与地震波存在差异且衰减速度更慢，当纵向地震激励趋近于零时，对应时间的中塔塔顶纵向位移和中塔塔根纵向弯矩却并不为零，说明纵向地震停止后结构仍然有一段时间处于纵向振动状态。

4．3 三向地震波耦合作用

三向地震波耦合作用下结构典型部位内力响应见表3所示，两桥塔纵向位移峰值包络图、主梁东西两侧中跨跨中竖向位移时程分别如图4（a）、（b）、（c）、（d）所示。

图3 James rd地震波纵向作用下结构典型部位响应Fig．3 Response diagrams of the typical site on the bridge under longitudinal effect of James rd seismic wave（Peak envelope of displacement and time－history curve）．

表3 James rd地震波三向耦合作用下典型部位内力响应值

三向地震波耦合作用下结构三个方向均发生明显振动。从表3可知，尽管结构几何对称，主梁西侧中跨跨中纵向弯矩较东侧大10%，中塔西侧主梁纵向弯矩较中塔东侧主梁大19．7%，东边塔根部纵向弯矩较西边塔大20．4%。笔者也曾将地震波反向输入模型，发现计算结果与上述结果基本相反，说明即使结构对称，其地震响应并不一定是对称的，还与地震波的输入角度有关。设计时应考虑地震输入角度的影响，选择最不利状态考虑。此外，对比表3和表2可以看出，地震波三向耦合作用下主梁东侧中跨跨中轴力、西边塔根部纵向弯矩均小于地震波纵向作用下结构的响应值，表明三向地震波耦合作用下结构响应值不一定为最大。因此三向地震波耦合作用结果未必就一定是结构的最不利受力状态，单维地震响应计算同样具有现实意义。

5 结论

利用有限元方法完成了桥梁在地震激励作用下振动状态的模拟，获得以下结论：

（1）桥梁基本周期为3．03s，第一振型为主梁反对称竖向弯曲，结构反对称效应较为明显，设计中应考虑竖向地震的影响；两边塔上主梁纵向漂浮使得纵向地震对中塔根部纵向弯矩和剪力影响均较大，设计时应配置足够的抗震主筋和箍筋。

（2）结构振动响应具有明显的方向性，与地震波的输入方向基本一致；但结构振动的衰减速度低于地震激励的衰减速度，地震激励基本停止后结构仍有一段时间保持着振动状态。

（3）考虑恒载作用初始状态对于判断地震作用是否控制结构构件的设计具有重要的意义。

（4）结构诸多对称部位的纵向弯矩相差较大，说明即使结构对称其地震响应结果也并不一定对称。

（5）三向地震波耦合作用下结构某些部位的响应小于地震波单独作用时的响应，因此三向地震波耦合作用未必就一定是结构的最不利受力状态，单维地震动响应分析同样具有非常现实的意义。

图4 James rd地震波耦合作用下结构典型部位响应图形Fig．4 Response diagrams of the typical site on the bridge under coupling effect of James rd seismic wave．

（6）地震作用初期结构地震响应时程曲线的走势与地震波谱走势具有一定的相似性，地震响应时程与地震波谱在统计意义上是否存在一种定量的数值关系，且这一关系是否仅与结构的类型相关，是一个值得进一步研究的问题。

［1］ 范立础．桥梁抗震［M］．上海：同济大学出版社，1997．

［2］ 叶爱君．桥梁抗震［M］．北京：人民交通出版社，2002．

［3］ Newmark N M．A Method of Computation for Structural Dynamics［J］．Journal of the Engineering Mechanics Division，ASCE，1959，85（2）：67－94．

［4］ 翟婉明．大型结构动力分析的Newmark－β显式算法［J］．重庆交通学院学报，1991，10（2）：33－41．

［5］ 中华人民共和国建设部，国家质量监督检验检疫总局．GB 50011－2001．建筑抗震设计规范［S］．北京：中国建筑工业出版社，2001．

［6］ 华孝良，徐光辉．桥梁结构的非线性分析［M］．北京：人民交通出版社，1997．

［7］ 任慧，尚守平，李刚．非匀质场地地震反应的模态叠加法解［J］．西北地震学报，2009，31（1）：26－30

［8］ Wang P H，Yang C G．Parametric studies on cable－stayed bridges［J］．Computers and Structures，1996，60（2）：243－260．

［9］ 高大峰，刘伯栋，张静娟．中承式钢筋混凝土拱桥自振特性分析［J］．西北地震学报，2009，31（1）：75－79．

［10］ 翟婉明．非线性结构动力分析的Newmark顶测——校正积分模式［J］．计算结构力学及其应用，1990，7（2）：51－58．

［11］ Clough R W，Penzien J．王光远，译．结构动力学［M］．北京：科学出版社，1985．

［12］ Park K C．An Improved Stiffly Stable Method for Direct Integration of Nonlinear Structural Dynamic Equations［J］．Journal of Applied Mechanics，ASME，1975，42（2）：464－470．

［13］ 梁庆国，韩文峰．强震区岩体地震动力破坏特征［J］．西北地震学报，2009，31（1）：15－20．

［14］ 重庆交通科研设计院．JTG／T B02－01－2008．公路桥梁抗震设计细则［S］．北京：人民交通出版社，2008．

Nonlinear Earthquake Response Analysis on Three－tower Cable－stayed Bridge Based on Newmark－βExplicit Scheme Direct Integration Method

YU Ming－qiu1，HU Bing2，ZHANG Dou－long3

（1．Bureau of Planning and Construction Administration of Panzhihua city，Sichuan Panzhihua 617000，China；2．School of Civil Engineering，Southwest Jiaotong University，Chengdu 610031，China；3．Chengdu Branch of Tanmu Information Technology（Shanghai）Co．，Ltd，Chengdu 610031，China）

U448．27

A

1000－0844（2012）03－0245－05

10．3969／j．issn．1000－0844．2012．03．0245

2010－03－08

中铁大桥勘测设计院横向课题

喻明秋（1983－），男，硕士研究生，四川遂宁人，主要从事桥梁抗震理论与应用研究．