Voronoi图和双曲线联合方法在地震快速定位中的应用①
2012-10-16王庆民刘希强沈得秀
王庆民,刘希强,沈得秀
(1.中国地震局兰州地震研究所,甘肃兰州 730000;2.山东省地震局,山东济南 250014;3.山东省地震工程研究院,山东济南 250021)
Voronoi图和双曲线联合方法在地震快速定位中的应用①
王庆民1,2,刘希强2,沈得秀3
(1.中国地震局兰州地震研究所,甘肃兰州 730000;2.山东省地震局,山东济南 250014;3.山东省地震工程研究院,山东济南 250021)
基于Voronoi图和地震震中近似满足双曲线分布,提出了一种联合应用V图和双曲线的地震预警快速定位方法。并对青海地震台网记录的地震进行了重新定位处理。研究结果发现,该地震定位方法能满足地震速报的精度要求,在时效性上也可满足地震预警的需要。该方法在地震预警方面有应用前景。
Voronoi图;双曲线;定位;地震预警
Abstract:Based on the concept of the Voronoi diagram and distribution of earthquake conforming to the distribution of hyperbola approximately,a new methods for earthquake rapid location in the earthquake early warning is presented that using the V-diagram and hyperbola jointly.The earthquakes recorded by the digital seismic network of Qinghai province are relocated with the new method.The result shows that the new method can meet the need of location precision and the timeliness of rapid report in the earthquake early warning,and is better than other ways.So the method has a good prospect of application in the earthquake early warning system.
Key words:Voronoi diagram;Hyperbolic;Location;Earthquake Warning
0 引言
地震预警技术是近20年新发展起来的地震监测新技术和震灾预防新手段[1-3],并已经开始在日本、美国、墨西哥、土耳其、意大利、瑞典、罗马尼亚和中国台湾等多个地震多发国家和地区得到了应用[4]。在这期间,各国科学家们通过不断探索,把确定地震参数的时间从几分钟缩短到了几秒钟。在某些可能的情况下,还可以为一些特定的区域提供这些参数并进行预警[2-3]。
地震预警[3]分为区域预警(如台湾[5]、墨西哥等[4,6])和现地预警(如日本的UrEDAS、南加州的Elarms等[7])。在区域预警中,我们可以通过整个台网记录到第1个P波与破坏性地震波(S波或面波)到达预警目标区域的时间差来进行预警。而现地预警则是利用P波到达后的最初几秒钟的信息确定预警震级,它利用P波比S波和面波传播速度快的原理,由P波的初期振动估计地震大小,确定震中位置并发出预警[3]。
根据以往的经验,我们发现决定预警成败的首要问题就是能否利用极其有限的地震台站和波形记录,快速准确地给出在精度上可以接受的震中位置。由于目前我国地震台网的布局和构成无法达到国外同等地震台网的规模和密度,而目前使用的传统地震定位方法又不能同时满足时效性和精度的双重要求[1,8-11],因此研究基于有限到时信息的近实时快速可靠地震定位方法是当前和未来地震预警系统中急需解决的关键技术。
本文主要是基于Voronoi图(简称V图或泰森多边形)和震中轨迹近似满足双曲线分布的联合方法来探索地震定位的一种新方法,这种定位方法在时效性和精度上能同时达到地震预警的实际需求,并有广阔的应用前景。
1 基本原理
1.1 Voronoi图
Voronoi图(以下简称V图)研究最早可追溯到1908年。G.Voronoi首先在数学上限定了每个离散点数据的有效作用范围,它是关于空间邻近关系的一种基础数据结构。1975年,Shamos和Hoey在IEEE Symposium on Foundation of Computer Science上联合发表的论文“Closest-point problems”是V图研究的里程碑,从此计算几何诞生[12],而V图在计算几何中占有非常重要的地位。V图在求解点集或其它几何对象与距离有关的问题时起的重要作用决定了V图可对区域进行合理的划分,并广泛应用于地震学,地理学,气象学,航天,核物理学,机器人等领域[13-14]。
本文根据离散分布的地震台站的地理坐标信息,将地震观测台站两两相连形成Delaunay三角网,寻找每个台站所涉及的所有有序目标三角形,对此三角形的外接圆心按空间位置进行顺时针或逆时针排序,然后依次连接圆心则生成台站的Voronoi单元(简称V单元)。遍历所有点,就生成所有台站的V图。这样生成的每个V单元中仅包括1个唯一的地震台站,而一旦某个V单元的邻近区域发生地震,我们就能唯一的确定这个区域。
1.2 双曲线定位方法
在平面直角坐标系内,到两个定点的距离之差的绝对值为常数(小于这两个定点间的距离)的点的轨迹称为双曲线,而震中到2个地震台站的距离差近似满足双曲线分布规律[15]。
设有2个台站,台站连线设为x轴,台站连线的垂线设为y轴,台站连线中点为坐标原点,台站间的距离设为2c km,则台站S1的坐标可表示为(+c,0),台站S2的坐标可表示为(-c,0)。假设2个地震台站间的介质为均匀介质,地震传播的P波速度为Vpkm/s,地震发生的时刻是T0,震源深度为Hkm,台站S1和S2到时分别是T1和T2(设T2>T1),震源到2个台站的距离分别为d1和d2(图1),则有

设H=0,则有
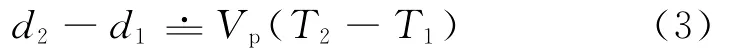
据此可知震中到2个台站的距离差等于常数,近似满足双曲线分布规律。根据双曲线变化规律和上述假定,可推导得出以台站S1和S2为焦点的双曲线顶点坐标是在这里我们设a=和y是震中坐标,则由式(3)可知:
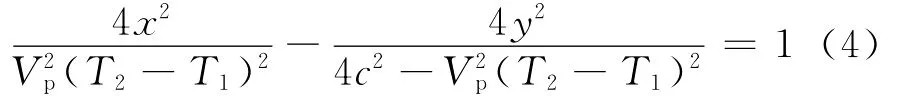
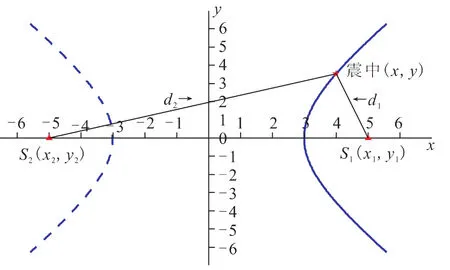
图1 双曲线地震定位方法示意图Fig.1 Diagram of the hyperbola location method for earthquake.
由于式(4)的震中(x,y)是在平面直角坐标系下推导的,而台站坐标一般情况下都是地理坐标,所以我们首先要把台站坐标转换为平面直角坐标(可通过墨卡脱投影),并在平面坐标系下进行坐标系的旋转和平移,得到平面直角坐标系下的真实震中轨迹,然后再把平面直角坐标系下的数据转换为地理坐标(可通过墨卡脱投影反变换)。
1.3 V图和双曲线联合定位方法
由于V图只是一个闭合的凸多边形,根据V图的性质可知,当某个台站最先记录到地震波时,震中一定位于这个台站构造的V单元中,但我们无法给出具体的震中坐标。而双曲线又是非闭合曲线,如果对数据不加限定的话则数据计算量非常大,无法达到快速测定震中的目的。所以我们提出利用V单元对双曲线数据进行裁剪,这将大大缩小数据计算量,加快计算速度,并可得到准确可靠的震中坐标。由于V图和双曲线都是在平面直角坐标下建立的几何图形,而台站坐标是大地经纬度坐标,为了保证这些几何图形在进行投影变换时不变形,我们将使用墨卡脱投影。
V图和双曲线联合定位方法系统流程如下:
(1)首先对地震台站的地理坐标数据进行墨卡脱投影变换,并用它构造平面直角坐标系下的由地震台站分布构造的V图。
(2)再根据所研究区域的地壳模型和3个地震台站的P波到时差,两两台站互相组合分别计算出3组a、b和c参数。
(3)判断这3组a、b和c参数能否构造双曲线方程(c>a>0),如满足,则求解该双曲线方程的数值解。
(4)对双曲线方程的数值解,在平面直角坐标系中进行坐标旋转和平移,并根据第1个台站的V图对双曲线数据进行裁剪,减小数据计算量。
(5)在特定的V图区域内计算双曲线的交点坐标。
(6)根据交点坐标构成的三角形,计算三角形重心。该重心的坐标即为震中位置。
2 资料及结果分析
2.1 研究资料及背景
青海数字化地震台网由48个速度型数字地震台站组成的虚拟台网。由于青海地域广阔,台网分布则相对显得稀疏,而青海又位于青藏高原内部,该区域地震多,强度高,进行地震预警研究具有一定的现实意义。
本文主要选取了青海地震台网记录到的最小震级3.0,最大震级4.8共计74次网内地震事件,利用基于V图和双曲线联合定位方法进行了重新定位。这些地震全部震中均位于网内。对于青海地区来说,我们取Vp为地壳平均速度6.58km/s[16]。图3给出了利用青海台网的地震台站建立的V图,图2为74次地震的震中分布(地震目录数据和重新定位结果)。
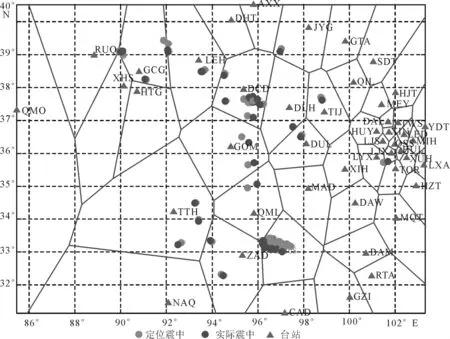
图2 青海地震震中分布及台网V图Fig.2 Distribution of earthquakes recorded by the Qinghai seismic network and its V map.
2.2 结果分析说明
(1)在表1和表2中我们给出了震中误差和区域预警时间的统计信息。绝大部分地震的震中误差小于35km,进行地震定位所需时间则小于30s。
(2)从图3中我们看出,74次网内地震重新定位结果与地震目录所给结果相比,误差平均26km左右,这主要是因为模型简化所致,但就其时效性而言,区域预警时间[3]平均为29s,足以满足地震预警的需要。

表1 青海台网地震重新定位的误差

表2 区域预警时间
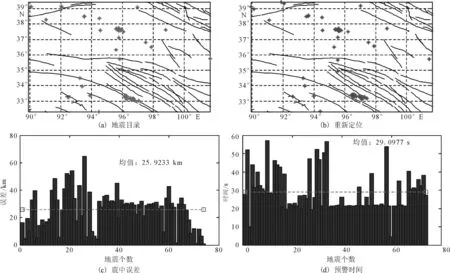
图3 青海地震的重新定位结果Fig.3 Relocation result for 74earthquakes in Qinghai province.
(3)图4给出了4个典型震例。震中分别位于DCD、TTH、GOM和YUS 4个台站确定的V单元内,括号内的数字表示地震波到时的先后顺序,框内的双曲线是由线条1-2、1-3、2-3组合以后得到的,三个双曲线交点重心坐标即为震中坐标。五角星是地震目录中给出的震中,圆点是重新定位的结果。虽然我们在快速定位中忽略了震源深度,但从定位结果我们看出,在满足时效性的前提下,定位精度足以满足实际需要,具有非常可观的应用前景。
(4)从图3中我们看出,本文的快速定位方法给出的重新定位结果就德令哈和玉树2个震群而言,其重新定位结果与实际观测还是比较吻合的,震中沿活动断裂线性分布。
3 结论
(1)本文所提出的地震定位方法在争取区域预警时间方面的优势非常明显,它可使地震预警的时间大大提前。
(2)由于只使用3个触发台站的P波到时,且速度模型简化为只是使用P波在地壳中平均速度值,定位精度不可能达到多台多震相地震定位的结果,但根据本文研究结果和震中平均误差来看,其震中结果仍有较大可信度和参考意义。
(3)由于V图是基于台网布局,所以台网密度和布局对定位精度及区域预警时间有较大的影响。
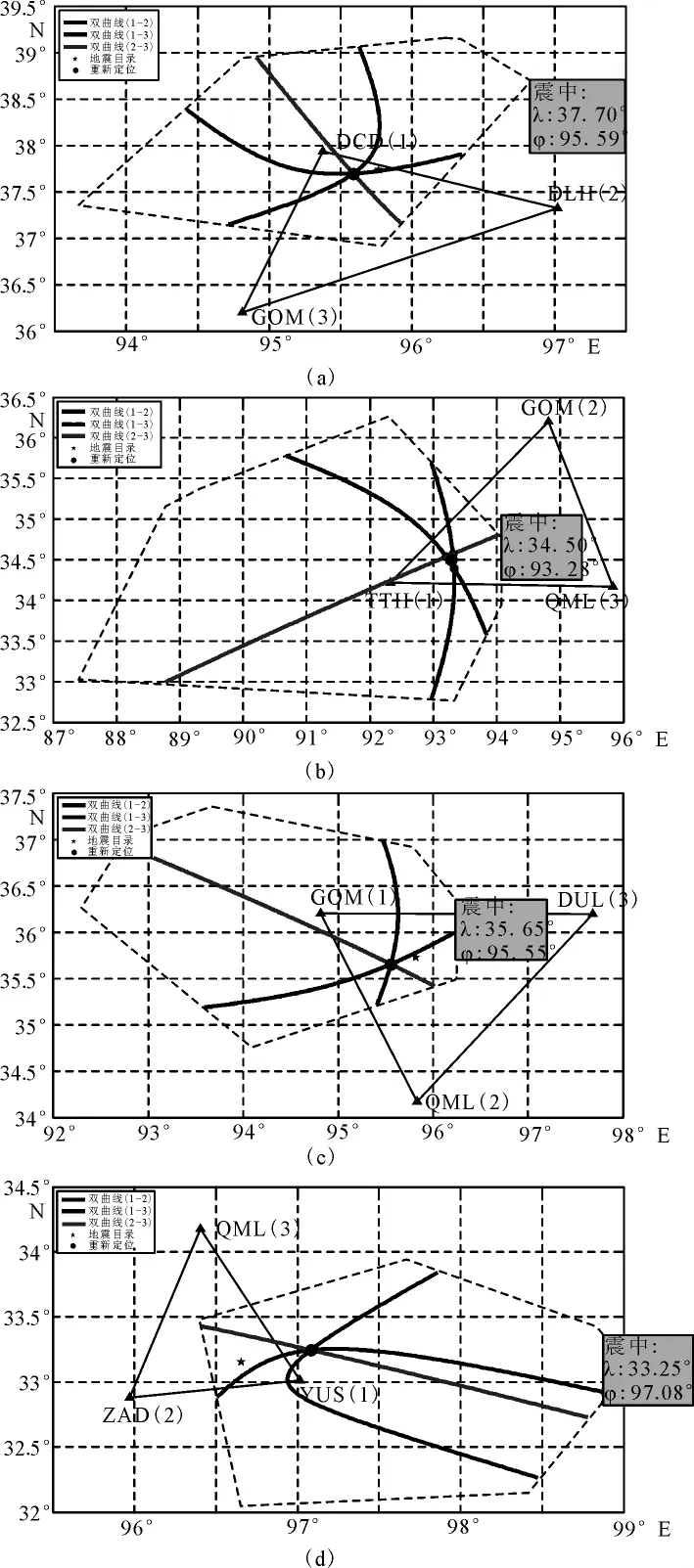
图4 典型震例重新定位结果Fig.4 Relocation results of some earthquake cases using the new way.
(4)虽然本文所讨论地震全部是网内地震,但自“十五”以后,我国地震台网覆盖范围有了质的提升,任何一个省份的区域台网都可以利用周边省份的台站建立虚拟网络,这样就不存在网外地震了(远离大陆的海洋地震除外)。
由于这种方法还在逐步的研究阶段,难免存在各种问题,今后的研究将在提高定位精度及解决深度问题上有所突破
[1] 黄媛,杨建思.用于地震预警系统中的快速地震定位方法综述[J].国际地震动态,2006,(12):1-5.
[2] Allen R M,Gasparini P,Kamigaichi O,et al.The Status of Earthquake Early Warning around the World An Introductory Overview[J].Seismological Research Letters,2009,80(5):682-693.
[3] Satriano C,et al.Earthquake early warning:Concepts,methods and physical grounds[J].Soil Dyn.Earthquake Eng.,2010,doi:10.1016/j.soildyn.2010.07.007
[4] Paolo Gasparini,Gaetano Manfredi,et al.Earthquake Early Warning System[M].Italy Napoli:Christine Adolph,2007.
[5] Nai-Chi Hsiao,Yih-Min Wu,et al.Development of earthquake early warning system in Taiwan[J].Geophysical research letters,2009,36:L00B02.
[6] Espinosa-Aranda J M,A Jimenez,G Ibarrola,et al.Mexico City Seismic Alert System[J].Seismological Research Letters,1995,66:42-52.
[7] Brown H M,Allen R M.Testing ElarmS in Japan[J].Seismological Research Letters,2009,80(5):727-739.
[8] 田玥,陈晓非.地震定位研究综述[J].地球物理学进展,2002,17(1):147-155.
[9] 杨文东,金星,李山有,等.地震定位研究及应用综述[J].地震工程与工程振动,2005,25(1):14-21.
[10] C Lomnitz.地震定位的三条原理[J].世界地震译丛,2006,(5):44-52.
[11] I Bondar,S C Myers,E R Engdahl,et al.地震台网的震中定位精度判据[J].世界地震译丛,2006,(4):38-55.
[12] M I Shamos,D Hoey.Closest-point Problems[A]∥Proceeding of the 16th Annual Symposium on Foundation of Computer Science[C].Washington DC.,USA:IEEE Computer Society,1975:151-162.
[13] Claudio Satriano,Anthony Lomax,Aldo Zollo.Optimal,Real-time Earthquake Location for Early Warning[A]∥Earthquake Early Warning Systems[G].Springer,2007:85-96.
[14] Claudio Satriano,Anthony Lomax,et al.Real-time Evolutionary Earthquake Location for Seismic Early Warning[J].Bulletin of the Seismological Society of America,2008,98(3):1482-1494.
[15] P Rydelek,J Pujol.采用双台子台阵方法的实时地震预警[J].世界地震译丛,2005,(3):1-6.
[16] 蔡学林,朱介寿,曹家敏,等.中国大陆及邻区岩石圈地壳三维结构与动力学型式[J].中国地质,2007,34(4):543-557.
[17] 马强.地震预警技术研究及应用[D].哈尔滨:中国地震局工程力学研究所,2008.
[18] 赵冰,刘希强.全球地震早期预警研究综述[J].西北地震学报,2011,33(4):392-402.
[19] Espinosa-Aranda J M,A Cuellar,A Garcia,et al.Evolution of the Mexican Seismic Alert System(SASMEX)[J].Seismological Research Letters,2009,80(5):694-706.
[20] Zollo G Iannaccone,M Lancieri.Earthquake early warning system in southern Italy:Methodologies and performance evaluation[J].Geophysical research letters,2009,36:L00B07.
[21] Richard M Allen,Holly Brown,et al.Real-time earthquake detection and hazard assessment by ElarmS across California[J].Geophysical research letters,2009,36:L00B08.
Apply of Voronoi Diagram and Hyperbola Methods on Earthquake Rapid Location
WANG Qing-min1,2,LIU Xi-qiang2,SHEN De-xiu3
((1.Lanzhou Institute of Seismology,CEA,Lanzhou 730000,China;2.Earthquake Administration of Shandong Province,Jinan 250014,China;3.Shandong Insititute of Earthquake Engineering,Jinan 250014,China)
P315.63
A
1000-0844(2012)03-0234-05
10.3969/j.issn.1000-0844.2012.03.0234
2011-09-19
家科技支撑计划课题(2012BAK19B04);中国地震局地震科技星火计划攻关项目(XH12029)
王庆民(1974-),男(汉族),河北乐亭人,工程师,研究生,研究方向为数字化地震波信息处理技术及应用.
