基于克里金法的地磁数据插值研究＊

于运治 田茂均

（海军潜艇学院 青岛 266044）

1 引言

对于水下载体，由于其不同于水上载体可以利用GPS等手段不间断提供高质量的位置信息，它所能利用的定位手段极其有限。地磁场不像无线电波那样在穿越水层时有衰减，它存在于大洋的任何深度。同时地磁场的场强和方向均是位置的函数，水下载体理论上可以通过测量地磁场要素与地磁图匹配得到唯一的载体位置。地磁场特点使得其有望成为水下载体导航定位的又一重要手段，因此也成为了目前各国重点发展的载体导航手段之一［1］。

地磁数据服务水下载体导航主要的方式就是构成载体航行区域的先验地磁图，达到这一目的最主要可靠的方法就是通过实测地磁数据法构建。载体活动区域通常空间尺度都非常大，要想实测如此大区域获取地磁数据无疑是一项巨大而且长远的工程。由于舰船等本身对磁场的影响和测量经费的制约，实测法不可能实现地磁数据很密集的测量，因此获得地磁图的精度和密度都有限。鉴于这样的实际情况，目前许多学者加大了对地磁空间数据插值算法的研究，力求通过研究出较好的插值算法弥补实测数据稀疏的问题实现地磁图的加密重构，从而提高地磁图的匹配概率和匹配精度。在众多的空间数据插值算法中，克里金法又成为了其中的佼佼者。

2 克里金插值法原理

Kriging插值法是一种用于空间插值的数理统计方法，以法国科学家Krige的名字命名，是一种空间自协方差最优内插算法，实质是利用区域化变量的原始数据和变异函数的结构特点，对未知样点进行线性无偏、最优估计［2］。它通过对已知样本点赋权重来计算未知点的值，不仅考虑距离还通过变异函数和结构分析来考虑已知点与未知点的空间方位关系，这样既反映了数据的空间结构变化又反映了变量的随机分布，还能描述误差信息，因此有着广泛的应用［3］。

克里金法由于采用的模型不同和优化时又引入的趋势、残差、协变量、协方差等因子，克里金法又产生了许多变种，这里主要以普通克里金法进行分析，其原理如下［4～5］：

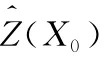
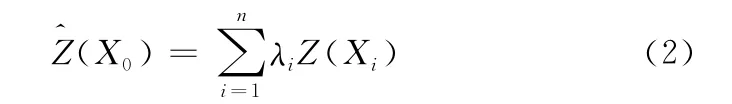
其中λi为已测量点Z（Xi）的权系数。上式中权系数的确定由克里金方程组决定，方程组可表示为

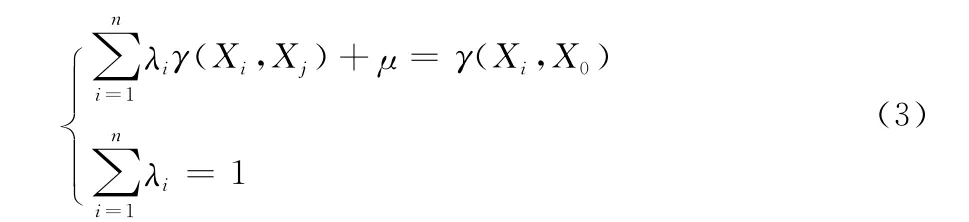
式中γ（Xi，Xj）为磁测量点的变异函数，μ为拉格朗日系数。变异函数的实质是一个协方差函数，是同一个变量在一定相隔距离上差值平方的期望。函数值越小，说明此段距离上该变量的相关性越好。因此变异函数可表示为

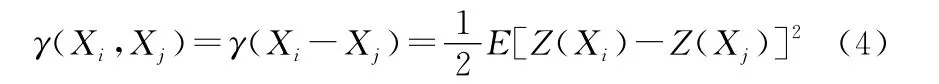
而当测点间的间距为h时有：

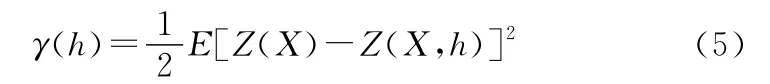
式中，h通常被称为滞后矢量；Z（X）是位置X处的值；Z（X，h）为与位置X偏离量h处的实测值。同时，克里金法还给出了估值误差的方差：

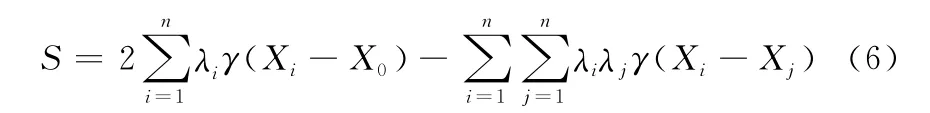
为求估计误差方差的极小值，将拉格朗日系数引入有：

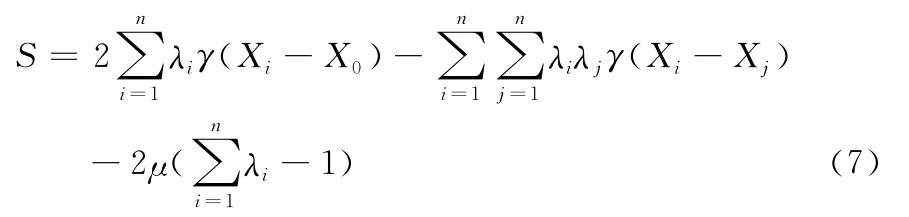
求解使估计估计误差方差最小有：

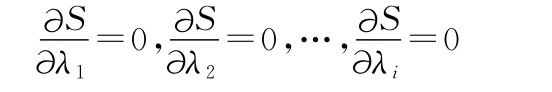
由此得到：

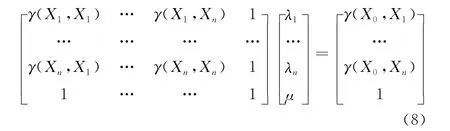
通过对上面方程的求解就可得到插值点的估值［6］。另外，克里金法还提供了一个检验其可靠性的指标，估计值与实测值之间的均方差σ2，它通过计算权系数和拉格朗日系数来得到：

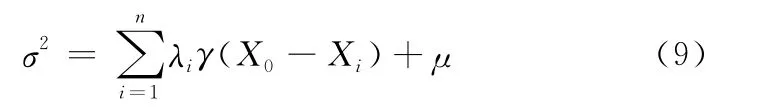
综上看出克里金插值法不但考虑估计点和已知点之间的距离和空间分布，还考虑了已知点与已知点之间的分布，因为相较其它插值法而言有一定的优越性。

3 实例分析

实例采用的数据是某海区5km×5km区域的实测磁异常数据，原始数据量为101×101，间距50m。为了验证插值方法的有效性，从中等间距的选取了11×11共计121个数据来作为“实验”数据。也就相当于用目前间距为500m的数据经过插值以后得到间距为50m甚至更密集的新数据。

图1是原始数据未经插值方法处理得到等值线图。

3.1 三种常用空间数据插值算法效果对比

在空间数据插值方法中主要有三种，一是最早也是最简单的加权反距离法，二是径向基函数法，三是克里金法。其中基于加权反距离法的改进又有了改进的谢别得法。而克里金法主要有普通克里金法和泛克里金，当然如之前所述引入的趋势、残差、协变量等因子还有许多变种。这里首先应用加权反距离法、径向基函数法和普通克里金法生成实验数据的等值线图。

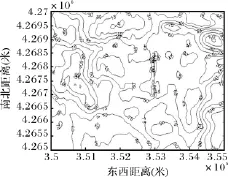
图1 原始数据等值线图

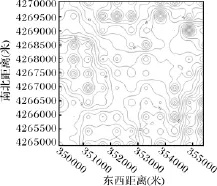
图2 实验数据加权反距离插值图

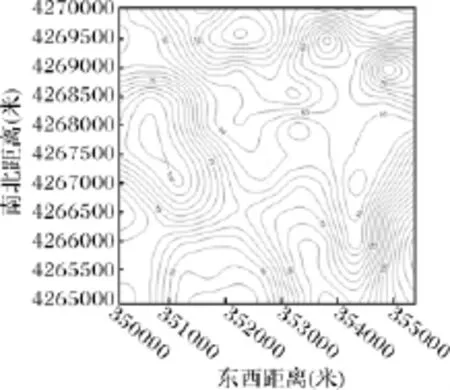
图3 实验数据径向基函数插值图

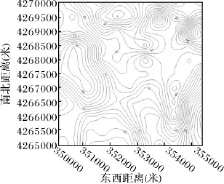
图4 实验数据普通克里金插值图

如上图我们可以看出加权反距离插值是不适用本例中地磁数据的，而径向基函数法和普通克里金法在直观上较为贴近实测数据。这里所采用的普通克里金法有一个前提就是默认数据是符合二阶平稳的，而且没有结算漂移。但是我们都知道，实测数据由于各种误差是肯定存在一定漂移的，所以普通克里金通常都需要改进，泛克里金法就考虑了数据的非平稳性质和数据存在的漂移。

3.2 数据空间结构分析

泛克里金法通过变异函数分析空间数据的结构特点。变异函数在前一节克里金法原理已有提到，这里不赘述。这里主要从实验变异函数角度实现磁异常数据这一区域化变量的变异函数建模。任何空间数据，在分析其结构时都要重点考虑其各向异性［11］。变异函数通过一些特点模型实现对数据各向异性的最大拟合，实验变异函数模型有指数模型、对数模型、线性模型、高斯模型、球状模型等等［7］。本例分析得出使用线性模型最能拟合数据特性，如图5所示。

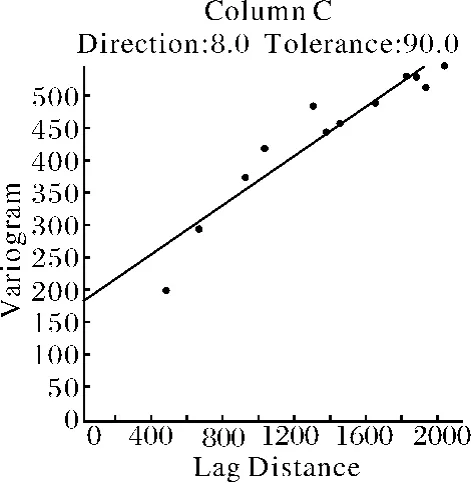
图5 实验数据变异函数线性模型

建模得出本例中数据的各项异性比为1.155，各项异性角度为142.6，倾率为0.1581。

3.3 交叉验证

空间插值法研究过程中通常都采用交叉验证法来评价插值算法的优劣程度。交叉验证的基本思路是重复从测点集合中去掉一个或者多个测点，用剩余测点集合利用需要评价的插值算法估算得到被删除点的值。然后用统计学的方法将测点上的估计值和实测值两组数据进行统计分析，评价插值方法的精度［8］；常用的交叉验证统计指标［9～10］有：

1）平均误差（ME）

2）标准差（SD）

3）均方根误差（RMSE）

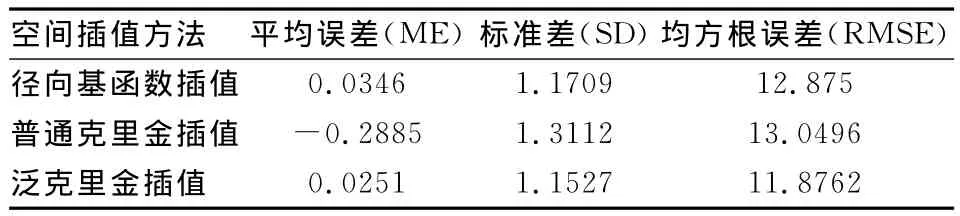
表1 插值方法交叉验证结果

4 结语

从上面的实例验证，可以得出结论。首先从直观的角度可以看出，如果值用实测的数据得出等值线，那么得到的等值线图不但不平滑，不利于匹配导航使用，而且“牛眼”现象也比较严重。另外也可以排除加权反距离插值法，因为相比较于普通克里金法和径向基函数法的插值效果，加权反距离法要远逊于这两者，而且比较原始数据可以看出，其所得到的等值线图不符合原始数据的性质特征。其次，就交叉验证的结果可以看出，在各项指标上，径向基函数法是要优于普通克里金法的。但是相比较与考虑了数据空间结构的泛克里金，径向基函数法又要稍逊于后者。

总结起来，通过插值的方法加密地磁数据，得到高密度的地磁数据，从而构建高精度的地磁图方法上是非常有效的。从交叉验证指标看，总体来讲误差都比较小，可以使用载体匹配导航需要。但是也可以明显看出原始数据在中偏右部有一个楔形峰值，几种插值方法都没有拟合出。问题可能存在于一是测量值有存在的野值可能；其二文章采用等间距取点方式，势必会再特殊峰值区存在插值信息不足的问题，这些有待下一步研究的解决。

［1］Goldenberg F.Geomagnetic navigation beyond the magnetic compass［C］／／Position Location and Navigation Symposium.Washington：IEEE，2006：684－694.

［2］侯景儒，黄竞先.地质统计学的理论与方法［M］.北京：地质出版社，1990：263－280.

［3］Soo－ChangPei，Ching－Min Cheng.Color image processing by using binary quaternion－moment－preserving theres holding technique［J］.IEEE TANSACTIONS ON IMAGE PROCESSING，1999，8（5）：614－628.

［4］张杨，康崇，吕金库，等.区域地磁测量实验及水下载体对周围磁场的影响分析［J］.中国惯性技术学报，2011，19（2）：205－208.

［5］靳国栋，刘衍聪，牛文杰.距离加权反比插值法和克里金插值法的比较［J］.长春工业大学学报，2003，24（3）：53－57.

［6］Rice H，Kelmenson S.Mendelsohn L.Geophysical navigation technologies and applications［C］／／Position Location and Navigation Symposium.April 26－29，2004：618－624.

［7］曾怀恩，黄声响.基于Kriging方法的空间数据插值研究［J］.2007，10（5）：53－57.5－8.

［8］武俊红，汪云甲.基于Surfer的煤矿等值线空间插值方法有效性评价［J］.中国矿业，2007，16（1）：108－110.

［9］汤刚安，刘学军，闾国军.数字高程模型及地学分析的原理与方法［M］.北京：科学出版社，2005，180－211.

［10］张晓明，赵剡.基于克里金插值的局部地磁图的构建［J］.电子测量技术，2009，32（4）：122－125.

［11］张仁铎.空间变异理论及应用［M］.北京：科学出版社，2005，273－284.