弹性地基梁问题的无网格伽辽金分析
2012-10-15李晓双赵慧明
李晓双,赵慧明,杨 敏
(中国矿业大学力学和建筑工程学院,江苏徐州221008)
0 前言
工程中,通常在结构底部设置基础,若假设地基为弹性的,则此类结构可简化为弹性地基梁问题。对于弹性地基梁问题,目前广泛使用的数值方法为有限单元法,且已取得了不少成果[1]。但有限元法是基于单元和网格的方法,会产生剪切自锁和所求函数的导数精度较低等问题。为了获得较好的结果,需花费大量时间在网格划分等前处理工作上,对于大变形问题,在求解中会导致网格畸变,使计算无法进行,此时需要重新划分网格,工作量很大[2]。无网格方法为近年来出现的一种新的计算方法,它不依赖于单元和网格,可以有效克服有限单元法存在的问题,在金属塑性成形、动态裂纹扩展、流固耦合等涉及到大变形、网格畸变等问题时具有很大的优势,并且与有限单元法相比,无网格法往往具有较高的精度,因此在很多方面得到了应用[3-5]。本文采用无网格伽辽金法(EFG)分析了Winkler弹性地基梁问题,并给出了具体算例。
1 弹性地基梁的基本方程
由Winkler地基模型可得到梁挠曲线方程

由微分方程理论,对于方程(1),其齐次形式通解为[6]
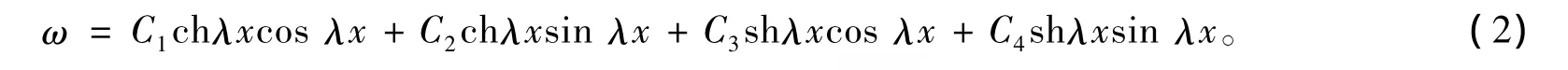
采用初参数法求解,得到任意载荷下弹性地基梁的计算公式[7]
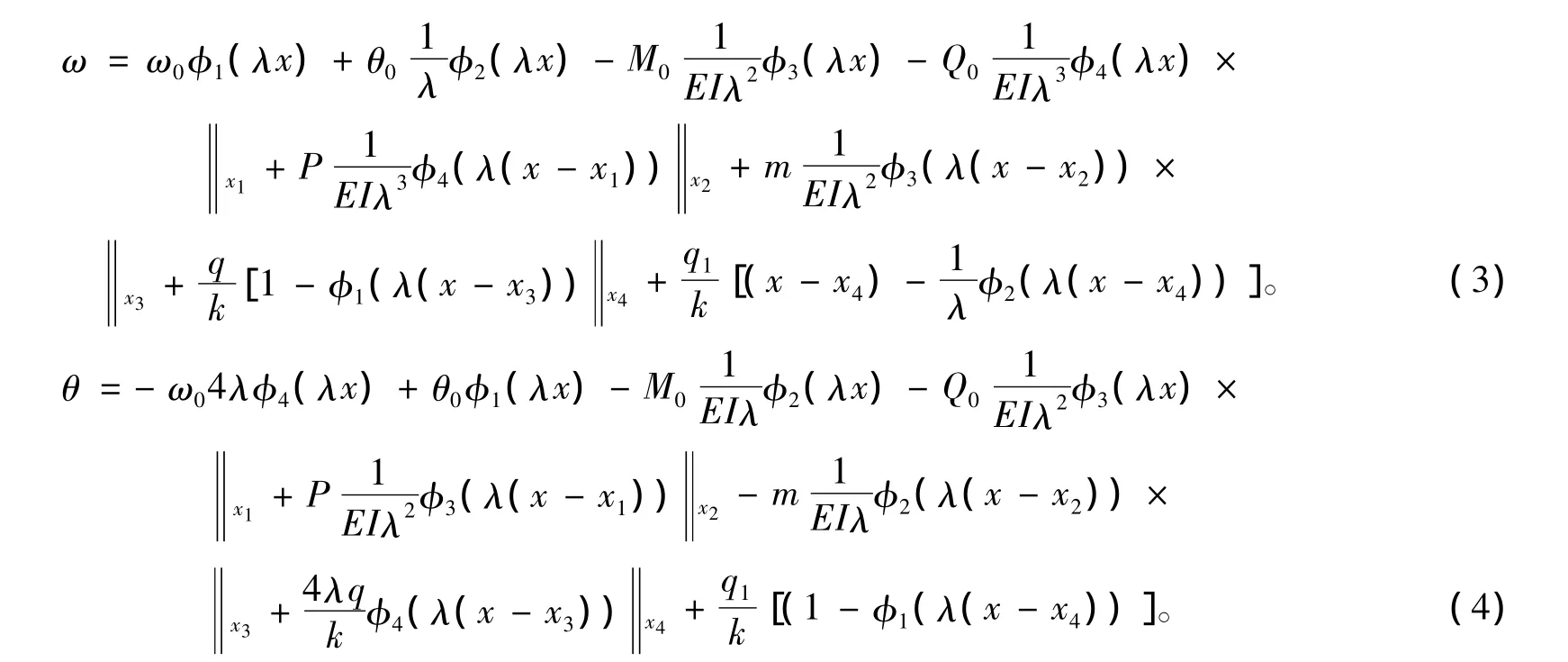
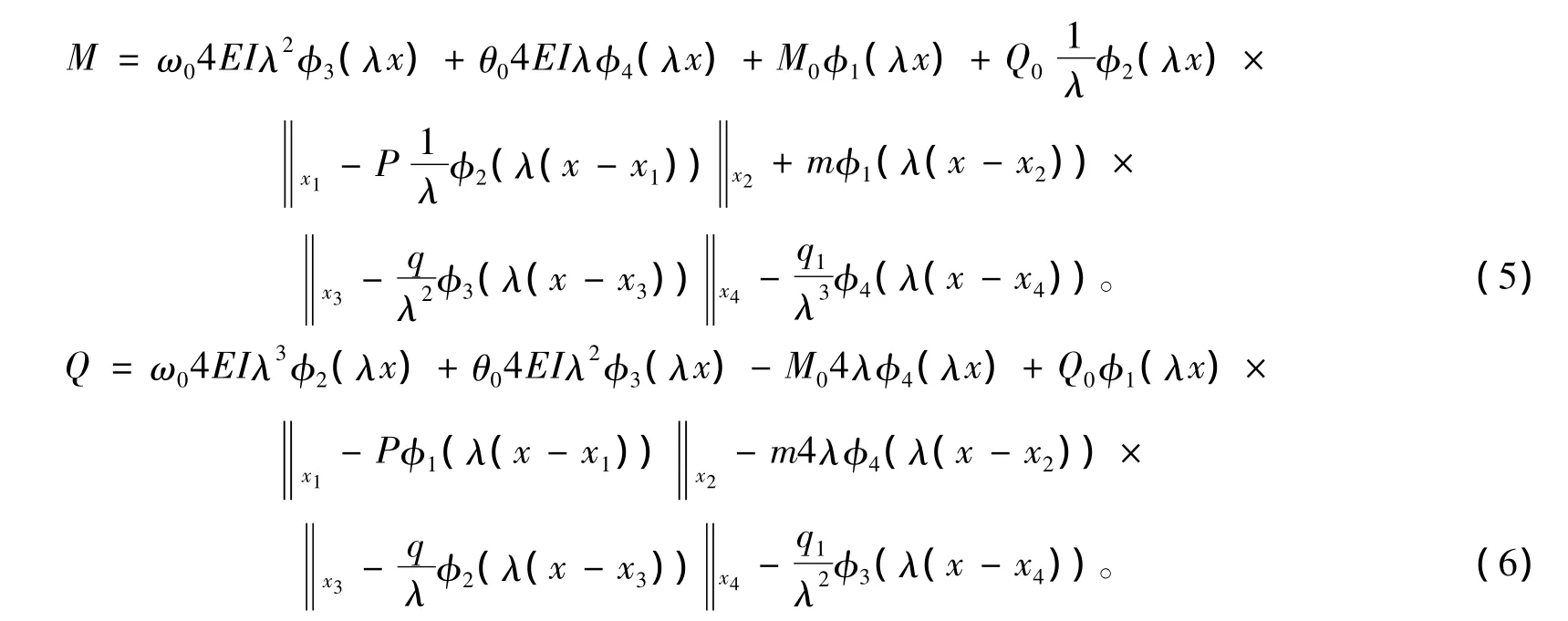

2 无网格伽辽金法
无网格伽辽金法(EFG)采用移动最小二乘方法构造形函数。
定义在x处的MLS近似表达式为
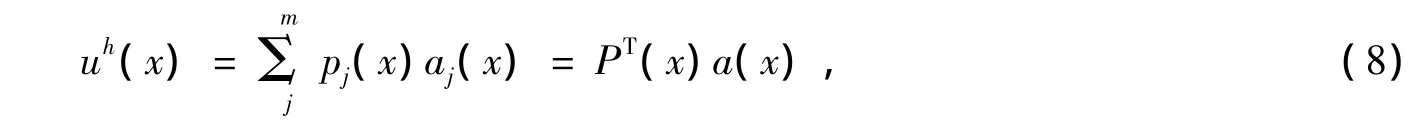
式中,pj(x)为多项式基函数;a(x)为待定系数,是坐标的函数。构造泛函,求解待定系数a(x),得到
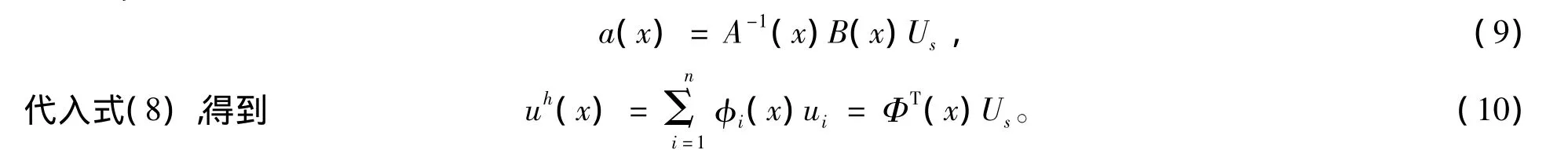
应用最小势能原理,得到弹性地基梁的能量泛函为
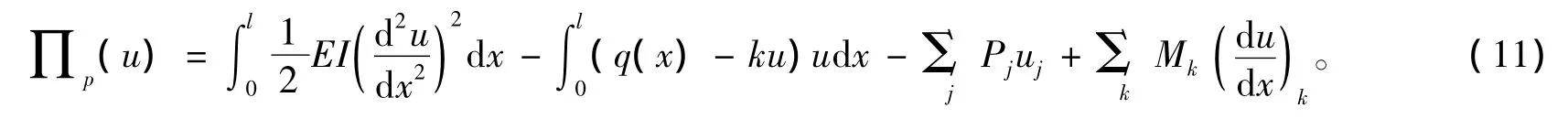
将式(10)代入泛函,并对泛函取驻值得到


Fc为集中力与集中力矩部分。
MLS近似不具备Kronecker δ函数性质,不能直接施加本质边界条件,通常采用罚函数法或者Lagrange乘子法施加本质边界条件。Lagrange乘子法可以精确施加本质边界条件,但会增加未知数数目,大大降低求解离散方程的效率[8-10]。因此,本文采用罚函数法施加本质边界条件。
在式(11)中添加位移约束项

式中α为惩罚因子,实际应用时常取足够大的正数。
对式(17)进行变分运算,最终得到的离散系统方程为

增加的两项为Kα和Fα。
Kα为总体惩罚刚度矩阵,其形式为
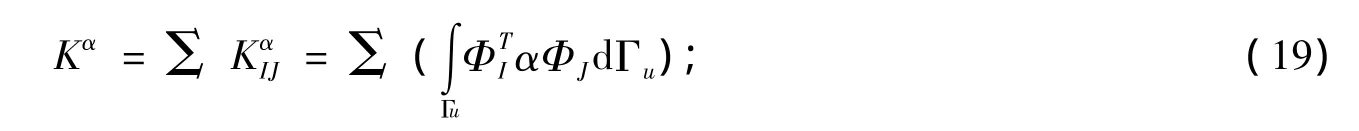
Fα为由本质边界条件引起的等效节点力,其形式为
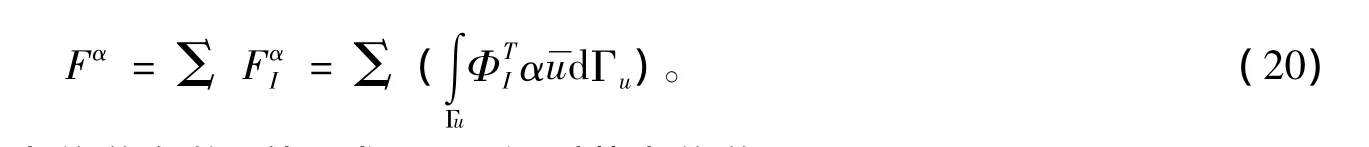
对式(18)进行求解,得到节点位移参数,利用式(8)可得到节点位移。
3 数值算例
图1为弹性地基梁,长度L=10 m,宽度b=1 m,深度 h=0.3 m,E=20 N/m2,地基的弹性压缩系数k=1.8×107N/m3,集中力P=400 kN,q=0.4 kN/m2。为便于编写程序,在算例中对梁采用规则网格节点布置,设置11个节点。
局部影响域的大小取值对结果影响较大,目前还没有相关的选取准则。本文采用文献[11]给出的值,取节点间距的3.0倍左右。局部积分域的大小取节点间距的2.0倍左右。由于模型具有对称性,在计算时可以只对前6个节点计算,结果见表1。
图1 数值算例模型

表1 挠度计算结果 ω/mm
从表1中可以看出:使用无网格EFG方法得到的结果与使用初参数解法得到的解吻合的相当好,最大误差不超过2%。当节点数增加时,误差会进一步减小。
4 结论
将无网格EFG应用于弹性地基梁问题,利用最小势能原理推导了离散系统方程,详述了实施方法和计算步骤。其求解过程同有限元法相似,但无网格EFG摆脱了对单元和网格的依赖,收敛较快。算例表明:用无网格EFG分析弹性地基梁问题,简便可行,精度较高。
[1]张晓玲.弹性地基梁的有限元分析[J].山西建筑,2008,34(27):137-139.
[2]于亚婷,杜平安,王振伟.有限元法的应用现状研究[J].机械设计,2005,22(3):6-9.
[3]曾媛,戴木香.无网格方法的研究现状与发展[J].山西建筑,2008,34(27):117-118.
[4]楼芬,邓建.无网格法及其在岩石力学与工程中的应用[J].地下空间与工程学报,2007,3(6):1014-1017.
[5]周维垣,寇晓东.无单元法及其工程应用[J].力学学报,1998,30(2):193-202.
[6]黄义,何芳社.弹性地基上的梁、板、壳[M].北京:科学出版社,2005.
[7]阎盛海.地下建筑结构中弹性地基直梁的初参数法[J].大连大学学报,2001,22(2):9-18.
[8]赵光明,宋顺成.无网格本质边界条件实现方法的研究进展[J].科技通报,2005,21(6):644-650.
[9]Liu G R,Gu Y T.无网格法理论及程序设计[M].济南:山东大学出版社,2007.
[10]Dolbow J,Belytschko T.An Introduction to Programming the Meshless Element Free Galerkin Method[J].Arch Comput Method,1998,5(3):207-241.
[11]夏平,龙述尧,胡玮军.弹性地基中厚板弯曲问题的无网格LRPIM分析[J].岩土力学,2010,31(2):656-660.
