变桨距风电机组最佳叶尖速比的拟合求取

张仰飞 ，李海峰 ，王伟胜 ，王瑞明 ，李少林

(1.中国电力科学研究院新能源研究所，北京 100192;2.南京工程学院电力工程学院，江苏南京 211167;3.江苏省电力公司调度与通信中心，江苏南京 210024)

风能密度低，风速变化频繁，风电机组变桨距技术应运而生，其实现方式[1-8]如下:通过对适时风速的测量，逻辑判断风速是低于额定风速还是高于额定风速.当风速低于额定风速时，桨叶的迎风角(桨距角)为0°，使桨叶能够最大限度地吸收风能;当风速高于额定风速时，桨距调节装置调节桨叶的迎风角，降低并保持吸收的风能在额定值，从而保证机组输出恒定(额定)的功率.

由于风力机(风轮)特殊的空气动力学特性，即使桨距角保持为0°也不能保证机组一定在最大风能捕获状态运行，必须通过机组的转速控制使机组转速和风速的比值尽可能保持在一个合理的定值——最佳叶尖速比，才能使机组吸收到最大的机械功率，这样的控制过程就是最大风能捕获控制.对风电机组而言，如何准确估算其最佳叶尖速比(即控制目标)，对于机组是否能够实现最大风能捕获控制，提高机组的发电效益，具有十分重要的意义.

笔者研究在测量数据有误差条件下的最佳叶尖速比求取问题，发现数据拟合方法结合特定的数学计算可以较准确地获得最佳叶尖速比.

1 变桨距风力机的数学模型

变桨距风力机模型[1-2]如下:

其中

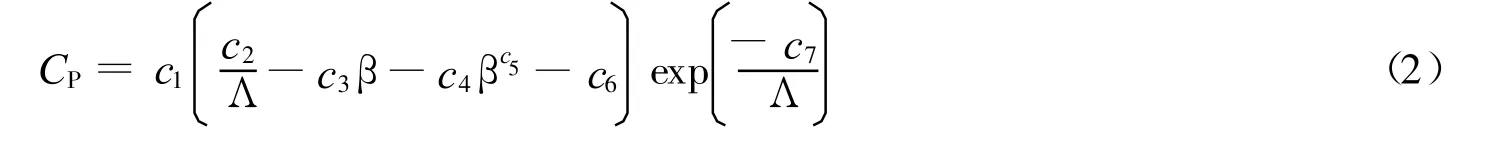
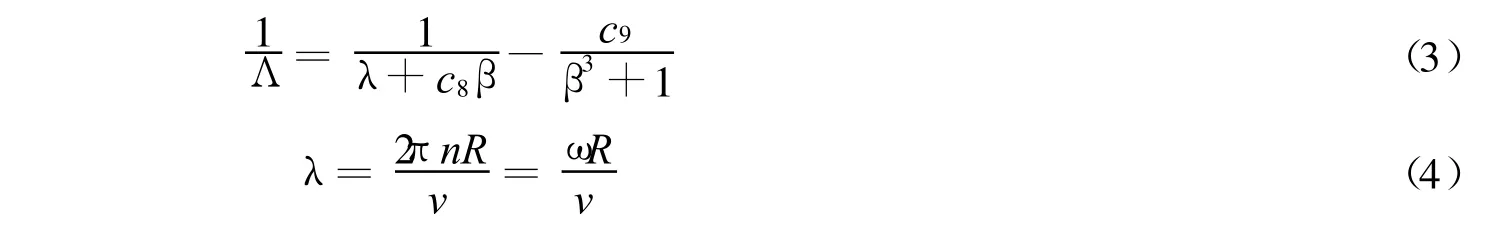
式中:CP——风能捕获系数;ρ——空气密度，kg/m3;S——叶轮扫过的面积，m2，S=πR2;v——叶轮的上游风速，m/s;PW——风力机吸收的机械功率;c1～c9——风力机参数(独立参数只有8个);λ——叶尖速比，即叶片的叶尖线速度与风速之比——中间变量;β——桨距角;R ——风轮半径;n——风轮转速;ω——转子的电角速度.

2 最大风能捕获的运行点条件

β=0°时，变桨距风力机 C P～λ曲线如图 1所示.对特定的风力机，其捕获的风能与转速、风速、空气密度等有关.由式(1)～(4)，对应于某个最佳叶尖速比 λ0会有1个最大的风能捕获系数CPmax，从而使风力机运行于最大风能捕获点PWmax.显然，最大风能捕获运行点是=0或=0，也即=0或=0.

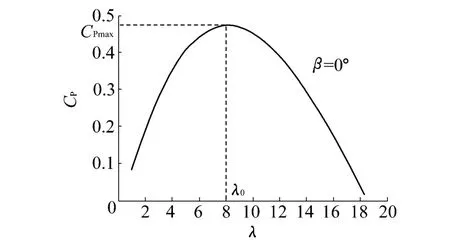
图1 β=0°时变桨距风力机C P～λ曲线Fig.1 C P～λcurve of variable-blade wind turbine under condition ofβ=0°

3 最佳叶尖速比的拟合求取思路

工程实际中，对应于低于额定风速的某一个风速v0，根据式(1)，期望风力机吸收的机械功率为PW=CPmaxρS.可见，在风速一定时，风力机能吸收多少机械功率取决于风能吸收系数C P的大小，也就是取决于风轮的转速或者是叶尖速比 λ的大小.

β=0°时可推导得

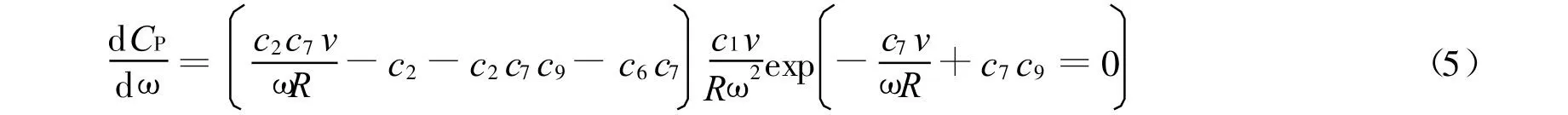
即

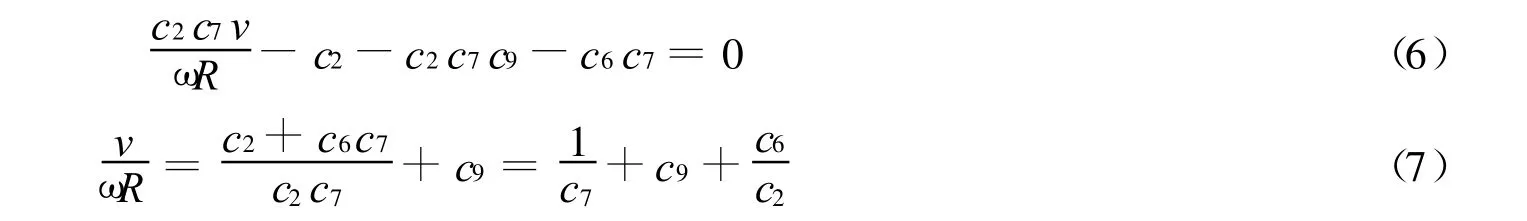
令 A=c2c1exp(c7c9)，B=(c2c9+c6)c1exp(c7c9)，则

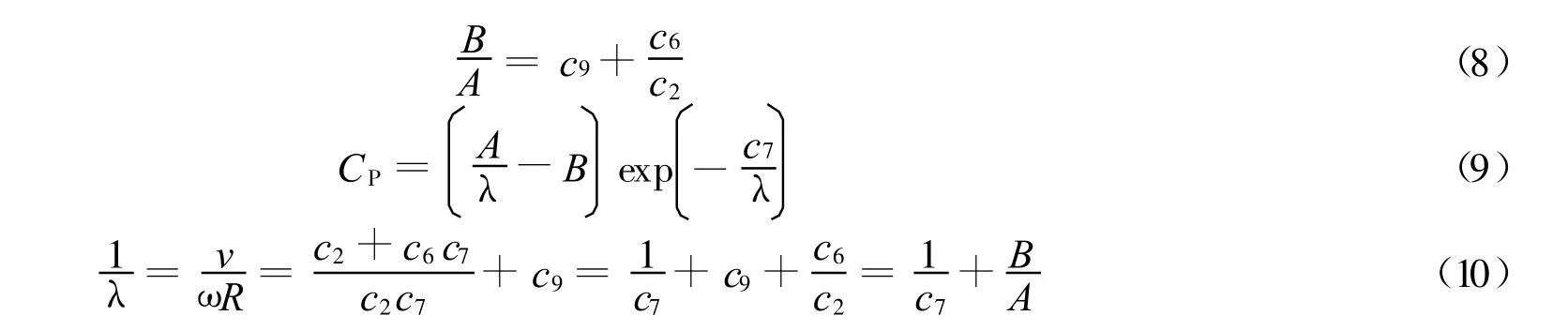
工程中可由式(1)及测量或计算的PW，ρ，v，ω，S来计算风能捕获系数CP，因 PW，ρ，v，ω，S的测量或计算难免存在一定的误差，必然会导致CP也有一定的误差.针对该CP存在误差的情况，如何求得对应于PWmax的λmax，由式(10)可知，如果能求得 c7，A 和B ，则 λmax可求 .

4 算例分析

[9-13]，设定 1组参数 :c1=0.32，c2=116，c3=0.4，c4=0.4，c5=0.1，c6=1.7425，c7=21，c8=0.08，c9=0.035.计算得 A=77.4131 ，B=3.87232，C=c7=21，λmax=10.241651.分析 CP值在一定误差条件下通过曲线拟合的方法求解λmax的准确度.

a.CP数据运用Matlab拟合函数[14]f(x)=(A/x-B)exp(-C/x)拟合，求得 A=77.41，B=3.872，C=21，拟合结果精确，拟合曲线如图2所示，2条曲线重合，看不出差别.根据拟合结果求得λmax=10.241874.

b.CP计算数据叠加±10%随机误差时，同样运用Matlab拟合函数f(x)=(A/x-B)exp(-C/x)，拟合求得 A=77.55，B=3.878，C=21.03，拟合曲线如图3所示.拟合结果令人满意，由拟合的 A，B和C值计算得λmax=10.25036.该结果与设定值相差很小，仅为0.00085%.

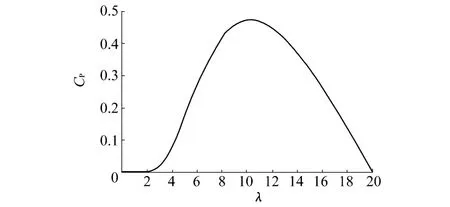
图2 无误差C P数据拟合曲线Fig.2 Fitting curve of C P without errors

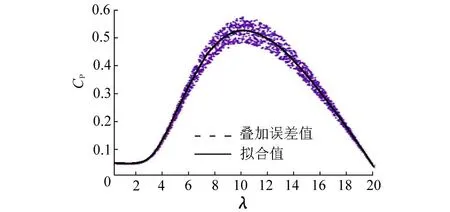
图3 ±10%误差C P数据拟合曲线Fig.3 Fitting curve of C P with±10%error

5 问题讨论

5.1 β≠0°时的情况

前文针对的是β=0°时问题的推导，工程实际中因桨距角直接影响机组的吸收功率，从而影响机组的出力，各厂家对机组的0°桨距角都会进行严格的校正.图4是2种机型变桨距机组低于额定风速时桨距角的实测结果，数据拟合结果如图中的线条所示.图4(a)中，β＞0.3°以上的数据分散特性明显，不符合桨距的机械惯性特征，可以判断是测量噪声.图4(b)中，0.14°＞β＞0.1°.

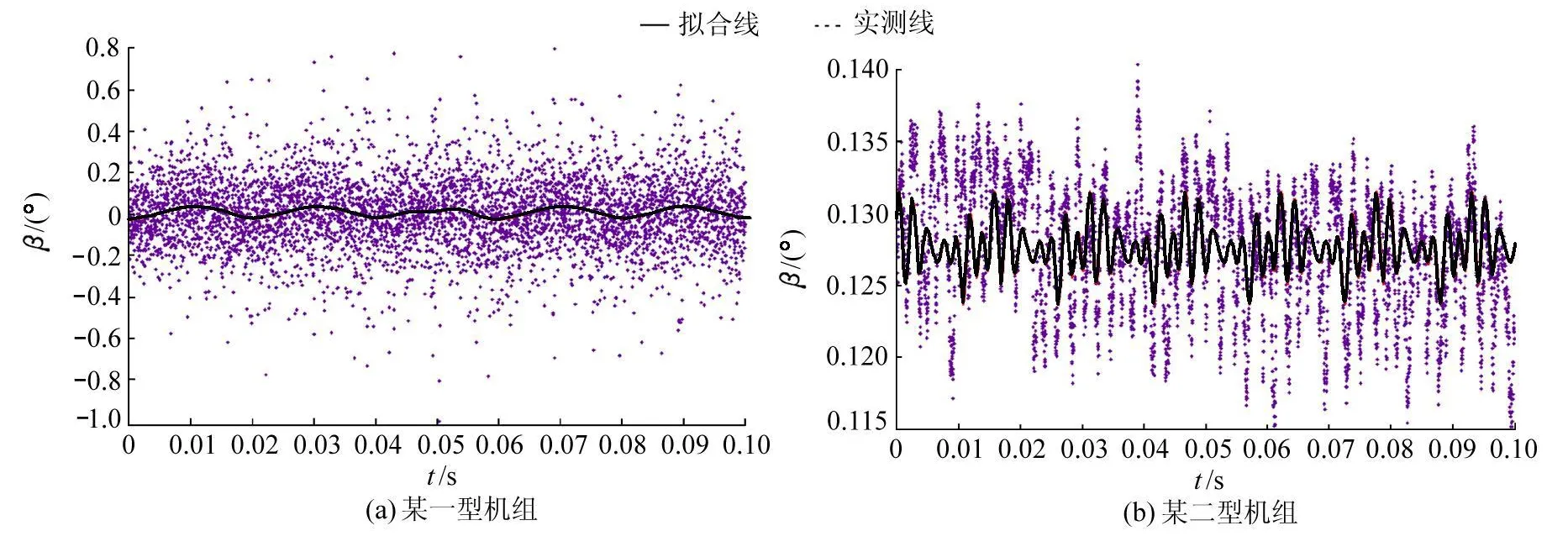
图4 机组低于额定风速时桨距角的实测结果Fig.4 Measured blade angle of wind turbines with speed lower than rated wind velocity

按照上述算例中的参数设定，可得 β=0°和β=0.5°时C P～λ曲线(图5).从图5可以看出2条曲线相差很小，最大点相差不到7%.可见，上述分析结论可以推广作为β≈0°时的情况使用.

5.2 风速v测量值的误差影响

风电机组利用计算机每秒采集1次来自风速仪的数据，每10min计算1次平均值，用于判断启动风速和停机风速，这样的风速数据并不精确，不能用来产生功率曲线[2].作为控制目标，也不能用该测量值通过式(4)来计算λ.相对而言，机组的转速能较准确地测量=0运行点可以通过调节系统的多次正调节和反调节实现，显然如果记录特定风速时的足够多组PWmax及 ω值就可以按照本文的方法拟合得到机组的λmax值，从而在后续的调节过程中不需要不断地正反调节.

6 结 语

本文分析中叠加的误差数据为服从正态分布的随机数据，由拟合结果来看，±10%误差C P数据拟合所得的A，B，C值和计算的λmax值都比较准确，工程上如果得到一定精度的CP数据即可以用上述方法拟合求解得高精度的 λmax，从而为最大风能捕获控制获得必需的目标参数.

用拟合方法求取最佳叶尖速比，要求数据具有一定的数量和密度，倘若数据的代表性不够则拟合误差就会增大.

辨识研究的目的之一是为控制需求提供准确的参数.研究工作表明:辨识工作可以根据应用目标的需要作适当调整，可以不辨识风力机的全部8个参数，只辨识部分参数的组合结果就能够满足控制目标实现的需要.

参考文献:

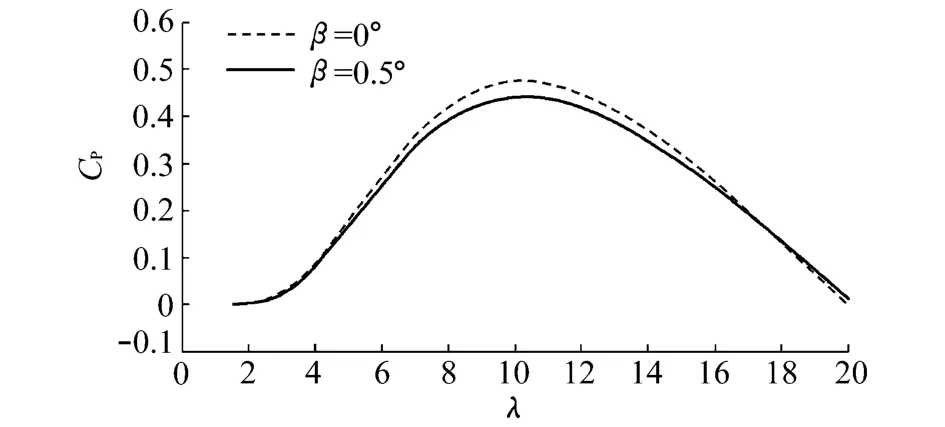
图 5 β=0°和β=0.5°时的 C P～ λ曲线Fig.5 C P～ λcurves under conditions of β=0°and β=0.5°

[1]叶杭冶.风力发电机组的控制技术[M].北京:机械工业出版社，2008.

[2]霍志红，郑源，左潞，等.风力发电机组控制技术[M].北京:中国水利水电出版社，2010.

[3]WU Feng，ZHANG Xiao-ping，GODFREY K，et al.Modeling and control of wind turbine with doubly fed induction generator[R].Georgia:PSCE，2006:1404-1409.

[4]MUHANDO E B，SENJYU T，YONA，A，et al.Disturbance rejection by dual pitch control and self-tuning regulator for wind turbine generator parametric uncertainty compensation[J].Control Theory&Applications，IET，2007，1(5):1431-1440.

[5]WU Feng，ZHANG Xiao-Ping，JU Ping.Modeling and control of the wind turbine with the direct drive permanent magnet generator integrated to power grid[R].Nanjing:DRPT，2008:57-60.

[6]刘军，何玉林，李俊，等.变速变桨距风力发电机组控制策略改进与仿真[J].电力系统自动化，2011，35(5):82-85.(LIU Jun，HE Yu-lin ，LIJun，et al.Design and simulation of an improved control strategy for variable-speed pitch controlled wind turbine driven generator system[J].Automation of Electric Power Systems，2011，35(5):82-85.(in Chinese))

[7]李立成，叶林.变风速下永磁直驱风电机组频率-转速协调控制策略[J].电力系统自动化，2011，35(17):26-31.(LI Licheng，YE Lin.Coordinated control of frequency and rotational speed for direct drive permanent magnet synchronous generator wind turbine at variablewind speeds[J].Automation of Electric Power Systems，2011 ，35(17):26-31.(in Chinese))

[8]宋卓彦，王锡凡，滕予非，等.变速恒频风力发电机组控制技术综述[J].电力系统自动化，2011，35(10):8-17.(SONG Zhuoyan，WANG Xi-fan，Teng Yu-fei，et al.Overview of control technologies for variable-speed constant-frequency wind turbines[J].Automation of Electric Power Systems，2011，35(10):8-17.(in Chinese))

[9]MONROY A ，ALVAREZ-ICAZA L.Real-time identification of wind turbine rotor power coefficient[R].San Diego:PICDC，2006:3690-3696.

[10]SENJYU T，OCHI Y，YONA A ，et al.Parameter identification of wind turbine for maximum power point tr acking control[R].Seoul:PICEMS，2007:248-252.

[11]THOMSENS ，ROTHNHAGENK ，FUCHSFW.Onlineparame ter identificationmethods for doubly fed induction generators[R].Rhodes:PESC，2008:2735-2741.

[12]IRIBAS-LATOURM ，LANDAU I D.Closed loop identification of wind turbines models for pitch control[R].Makedonia:MCCA，2009:1263-1268.

[13]AIMANIS E.Practical identification of a DFIG based wind generator model for grid assessment[R].Ouarzazate:ICMCS，2009:278-285.

[14]王正林，王胜开，陈国顺，等.MATLAB/Simulink与控制系统仿真[M].北京:电子工业出版社，2008.