数控加工中进给速度的优化方法研究
2012-10-12陈德存
陈德存
CHEN De-cun
(温州职业技术学院 机械工程系,温州 325035)
0 引言
当刀具在经过曲率变化较大的一些刀位段时,由于机床伺服系统能力的限制,机床加减速达不到NC指令要求的加减速要求,容易出现“过切”与“欠切”现象,如图1所示。这主要是由于切入曲率变化剧烈时,机床各轴移动的速度突然加快,这样会导致伺服系统驱动功率不足,使系统整体速度下降,容易出现爬行,从而造成欠切和啃切零件表面的现象[1]。数控编程的进给速度只是个参考值,实际加工时速度由系统内置的速度控制环进行实时的控制。但由于的加工程序均为微小直线段,要实现速度平滑需要预读多段[2],这就对数控系统的处理速度要求很高,普通的数控机床无法在短时间内完成如此大的计算工作,因此有必要优化刀位文件中的进给速度以减少加工中啃切现象。

图1 拐角啃切现象
1 数控系统加减速控制原理
在数控制机床装置中,为了确保机床在速度快速变化的时候,不产生跳位、过冲或振动,必须控制进给伺服电机的脉冲频率或者电压,以保证加在伺服电机上的脉冲频率逐渐变化。加减速有前加减速和后加减速之分,前加减速控制放在插补器的前面,后加减速控制放在插补器的后面[3]。
前加减速的控制对象是工作台进给速度F,它的工作原理是在插补前预先计算出各坐标轴的进给量△X、△Y,然后转换为进给电压或脉冲以驱动电机[4]。这种方法加工精度较高,但运算量较大。后加减速的算法放在插补器之后,它的控制的是各运动轴的速度分量。它不需要预算减速点,在插补输出为零时开始减速,并通过延迟一段时间的法逐渐靠近程序段的终点。该方法的缺点是:加工曲线轮廓有误差,并且当轮廓的曲率在急剧变化时,后加减速无法预见,从而会产生过切现象。目前后加减速控制方式在高精加工中很少使用。
2 针对前加减速控制系统机床进给速度的优化
机床各轴的进给速度优化方法类似,这里以X轴的优化为例。
由加速度公式v2=+2a(x-x0)可推出:
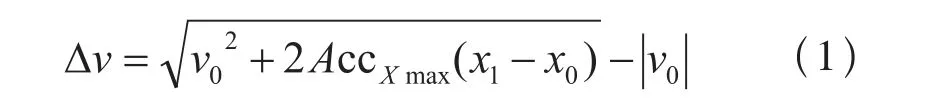
其中,(x1-x0)为X轴工作台在两相邻刀位点上的位移量;
AccXmax为X轴最大加速度。
由公式可以计算出两相邻刀位点上的速度最大增加量(减小量)。如果速度增加量(减小量)大于△v,那么机床就无法响应该指令速度,从而可能造成该处表面造成较大的误差。因此我们就认定该段的NC指令设定的速度不合理,需要对该段的速度进行优化,使这段速度度的变化量小于等于△v,这就是优化X轴工作台移动速度时的基本思路。
2.1 对X轴工作台赋初值
由于原文件中刀位文件并的进给速度本身并没有多少实际意义,在这里彻底舍弃,而重新赋值X轴工作台的速度。这样做增加了方法的通用性以及可操作性。
l)在需要优化的刀位段上的进给速度给定一个新的值,该值可以看作是设定“最大进给速度”。在对优化后的刀位文件的进给速度都不会超过这个速度。得到的进给速度如图2(a)所示。
2)计算各相邻刀位点之间的实际移动距离。得到的X轴移动距离如图2(b)所示。
3)由时间-速度公式计算各相邻刀位点之间X轴工作台的运动速度如图2(c)所示。
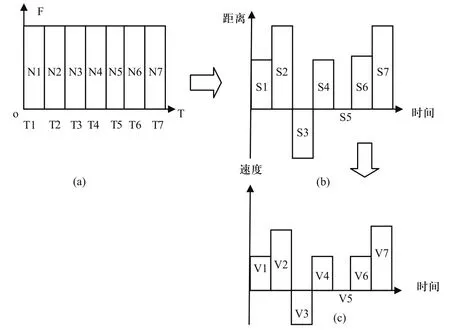
图2 X轴工作台赋初值步骤
2.2 进给速度的优化点的判断
根据X轴的加速度AccXmax对机床的实际运动速度作出预测,并对其中不合理刀位段的速度进行优化。下面以图2中N1、N2两刀位段上的运动为例。
N1段初始进给速度v1,N2段初始速度v2。机床在行N1终点时N2段的指令时,X轴工作台以AccXmax的加速度开始加速。当运行N2段的末端时会出现两种可能:
1)如果N2刀位段上的距离足够大,匀速运动到N1段的终点。
2)如果N2刀位段上的距离较短,X轴工作台在N2段的终点时所达到的速度由公式(1)确定。

图3 查找X轴作台中速度需要优化的刀位点
对于1)这种情况,就不需要对刀轨文件的进给速度进行优化,机床完全可以按照刀位文件指定的速度完成该刀位段。如果是2)这个情况,机床工作台无法完成NC指令的速度,这种状况下,就需要对刀轨文件的进给速度进行优化。
优化前首先要寻找需要优化的速度所在的刀位段。步骤可分为以下几步:
1)计算Ni点与Ni+1点上速度的差值;
2)计算X轴相邻两刀段位的最大速度改变量△V,如果该值小于第一步的计算结果,则进行下一步,否则说明该处的速度不需要优化;
3)如果 VNi+1>0,并且 VNi+1>VNi,或者如果VNi+1<0,并且 VNi+1<VNi点则说明 Ni+1 点的速度需要优化。
图3说明了使用这种方法对X轴工作台刀位点上的速度进行查找和优化的基本流程。
2.3 进给速度优化方法
优化时按照如下原则进行:
如果VNi+1>0,那么应该减小该点处的速度;
如果VNi+1<0,说明在该刀位段上是反向运动,那么应该提高该点处的速度。
总原则是要使|VNi+1|→0。
优化后Ni+1点处的速度为:
当VNi+1速度方向与 VNi速度相同时:
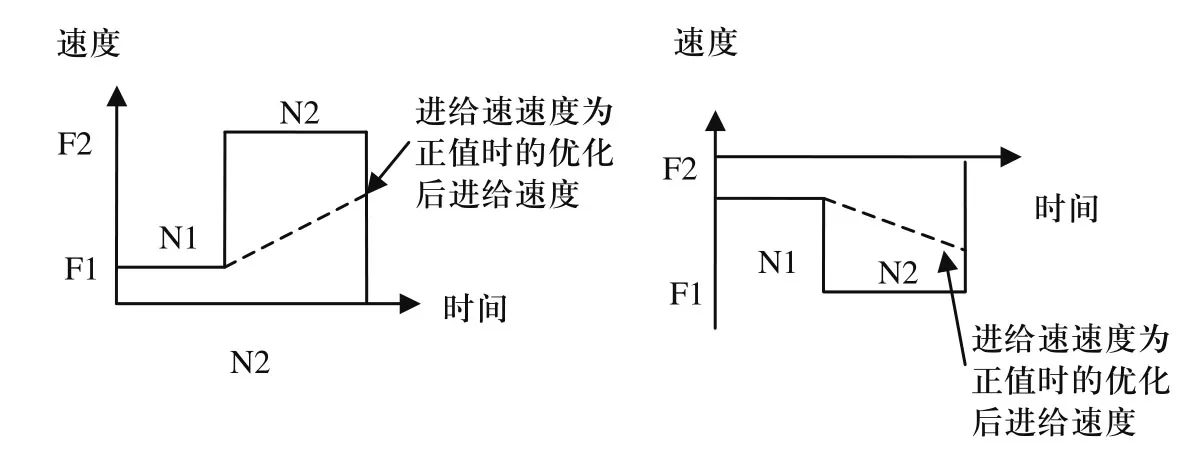
图4 相连段位进给速度相反时的优化结果
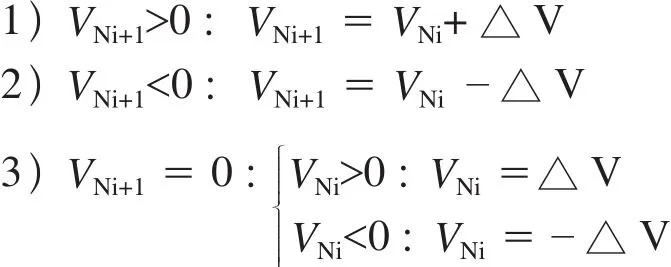
当VNi+1速度方向与VNi速度相反时:
为了能够保证优化后的速度方向不发生改变,应该同时修改Ni +1点与Ni点处的速度。
1)|VNi| > V/2 且 |VNi+1| > V/2 :VNi= ± V/2,VNi+1=±V/2(如图5(b)所示);
2)|VNi|< V/2:VNi不变,VNi+1= ± V-|VNi|(如图 5(c)所示);
3)VNi+1< V/2 :VNi+1不变,VNi=± V-|VNi+1|。
通过优化计算,如果原本两个速度的绝对值都较大,优化后,它们的绝对值都取到了尽量大的值;如果中有一个相对较小,优化后,速度绝对值较小的保持不变,仅把绝对值较大的那个点处的速度向零速度“靠近”。
这样通过以上方法对所有的刀位点上的速度进行一次寻找并且优化后,可以重新得到的X轴工作台的进给速度,优化后的进给速度如图6所示。从图中可以看出,优化后各刀位的进给速度变得相对比较平滑,但是仍有一些点为段上速度的变化过大(如图6中的N4段,其减速度过大)。因为本次优化只是对加速度过大的刀位优化,并没有对速度绝对值变小的刀位进行修改。所以下一步需要把这些速度绝对值变小的刀位段上的筛选出来,并有进行二次优化。
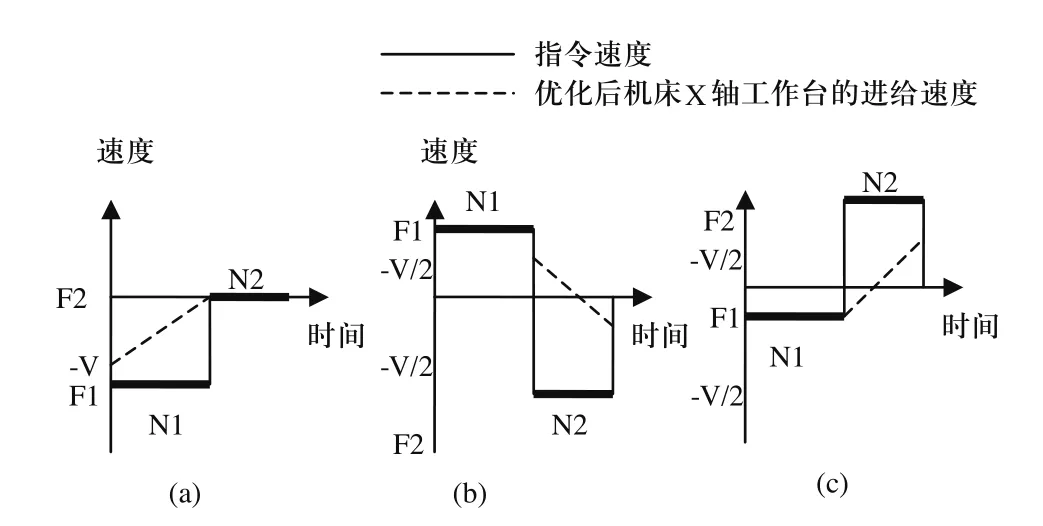
图5 相连段位进给速度相同时的优化结果
二次优化的寻点与第一次不同,这次的方法是从最后一个刀位段开始,并它相邻前一刀位段上的速度进行比较,比较的方法与第一次的方法完全一致。寻找这些速度变化过大的刀位点,非常适合用计算机程序完成,仅需要将原来存放这些刀位点的速度的数组按照从后向前的顺序逐个检索,找到并优化。给出X轴工作台的进给速度经二次优化后示意图,如图7所示。

图6 对X轴上作台进行了一次优化后得到的进给速度
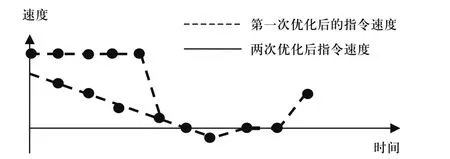
图7 X轴经两次优化后得到的进给速度
从图7中可以看出,经过两次优化,X轴工作台在各个相邻刀位段上速度的变化变的比较平滑。这样机床X轴的伺服在执行当前刀位段时就能够预读后面到位段得进给速度,假设机后面有一刀位段速度为反方向的,那么无论与当前的刀位点相隔多少个刀位,机床都有对X轴的进给速度减速,从而保证在所有的刀位点上都不会发生过切现象,同时保证机床的加工效率。
对其他轴工作台的进给速度化与X轴工作台优化方法一样,即先赋初进给速度给其他相应的工作台,在的初始进给速度基础上,按照X轴工作台进给速度的优化方进行优化。其优化的方法与思路完全一样,这里就不再重复。
3 航空发动机叶片四轴加工刀轨进给速度的优化
现在以发动机叶片为例说明刀轨优化的过程,如图8所示。是叶片类零件是发动机的重要零件,广泛应用于航空领域,其表粗糙度和精度要求高,生产制造难度大,目前普遍采用大型多轴联动机床对其进行加工。
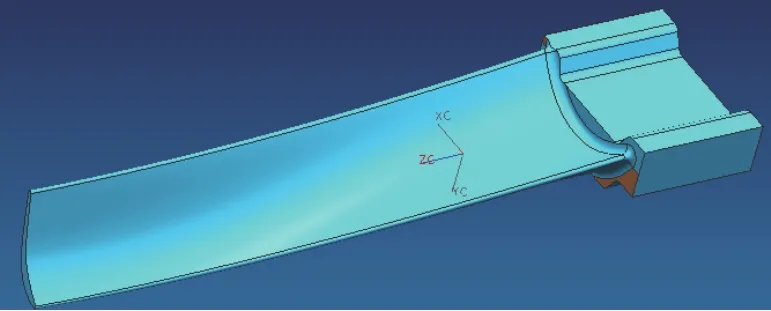
图8 航空发动机叶片
以本文中的UG的CLS刀位文件为例。CLS文件是UG加工刀轨后置处理产生文件,该刀位文件可以使用于多种多种加工软件。CLS文件记录了刀具的名称、位置、切削加工时的进给速度、轨迹的显示颜色及主轴的转速等。
设定最大进给速度为400mm/min,假设X、Y、Z各轴的最大速度为12000mm/min,最大直线加速度为0.38m/s2,A轴的最大转动速度为4500deg/min,最大角加速度为2.58deg/s2。
先计算刀具总的进给速度进行,其计算公式为:
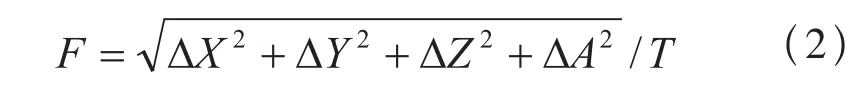
式中T为上一节中计算出的A轴转动时间。得到的F就是NC代码指定的进给速度。
按以上方法对CLS文件中的进给速度进行优化。下面两段代码代码是修改前后生成的G代码:


从上面两段代码对比可以看出,在之前速度变化过大的地方插入了新的进给速度,使得切入和切出叶片缘头部位时具有较低的进给速度,这对于减少机床系统的运算量,降低伺服延滞有着积极的意义,从而不易出现啃切现象。将优化前后G代码分别输入到用VERICUT软件模拟现实加环境建立起来的机床模型进行仿真,结果如图9所示。
4 结束语
目前,国内对数控加工的轨迹生成方法已经研究比较多,但是对如何生成更加光顺合理的轨迹应用并不多。本文通过介绍CNC控制系统加减两种速控制方式,提出对常用的前加减速控制进行优化,使输出位文件的进给速度改变量变的平滑光顺,这样减少了数控系统计算量,降低了数控伺服系统产生延滞时间,从而减少了过冲、欠切现象,最后通过VERICUT软件仿真对比加工航空叶片边缘表面质量有明显很大的提高。该方法对提高工件质量,延长机床、刀具使用寿命有积极的意义。
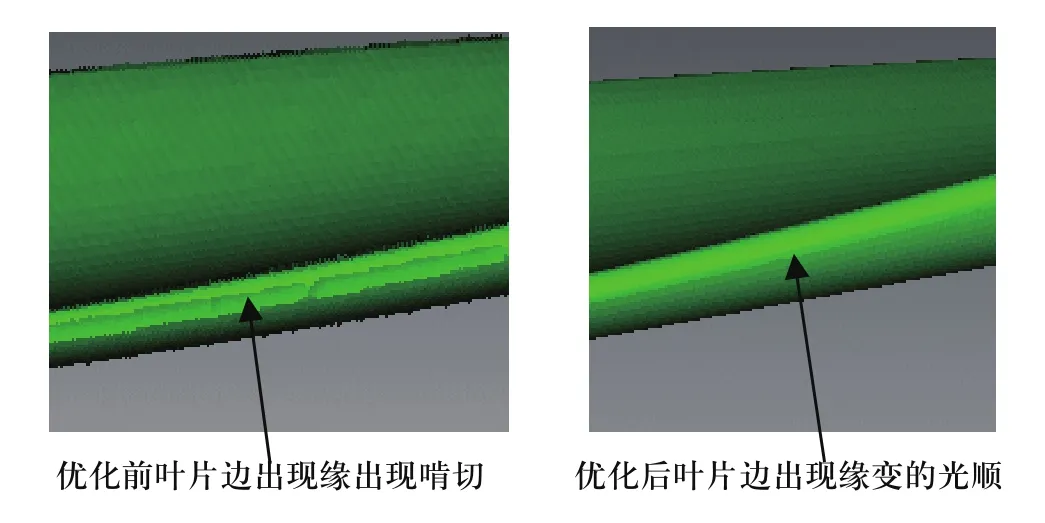
图9 叶片四轴加工优化前后边缘部位对比
[1]曹利新, 马晓嘉. 五坐标加工整体叶轮粗加工刀位规划[J]. 大连理工大学学报, 2008, (01) .
[2]张得礼, 周来水. 数控加工运动的平滑处理[J]. 航空学报, 2006, (01) .
[3]李曦, 唐小琦, 陈吉红, 周济. NC伺服的加减速控制算法的研究与实现[J]. 机床与液压, 2000, (03).
[4]谈勇. 高速高精度雕铣机数控系统的研制[D]. 合肥工业大学, 2004.
