基于Zernike矩的亚像素边缘检测改进算法

胡树杰

HU Shu-jie

（沈阳理工大学 信息科学与工程学院，沈阳 110168）

0 引言

物体的边缘无论是对人类的视觉系统还是对数字图像处理技术都具有非常重要的意义，它是图像的基本特征。一般有三种亚像素边缘定位方法：分别是拟合法，插值法和矩法[1～3]。对于拟合法，是根据已给出的边缘模型，通过拟合图像的灰度范围得到亚像素边缘位置[4～6]。该法准确性高，但缺点是比较耗时。插值法是依据实际图像的灰度分布，通过插值图像数据完成了亚像素边缘定位，该方法优点是节省时间，但对噪声比较敏感[7,8]。由于矩是积分算子并对噪声不敏感，因此矩法成为了一种被广泛应用的方法。

Zernike矩和Zernike多项式被广泛应用于图像处理应用中。Zernike矩是以Zernike多项式为核函数的矩，Zernike多项式构成了一个完备的正交集。Zernike多项式的正交性使得Zernike矩互相独立，Zernike矩的幅值对旋转是不变的。因此Zernike矩使它在特征表达式和低的噪声敏感度等方面具有较大的优越性，并且不用考虑形状的较小变化。另外由于基是正交的，它们有较小的信息冗余[9～11]。

但在高阶矩中，尽管它们的整体性能优越，仍然具有较高的计算成本和数值不稳定性。为了降低计算成本，Chong等人开发出一种命名为q-recursive的新方法[12]，另一种有效的方法是Prata法[13]。在本文中，重新分析了Prata递归法，提出来一个改进的Prata算法。通过分析，改进的Prata算法在每次递归中算术运算最少，因此在所有方法中改进的Prata法速度最快。

1 ZMs递归方法的计算

1.1 Zernike矩

在单位圆中图像函数f(x,y)被定义在p和q的二维坐标系中

这里f(x,y)是大小为N×N离散区域中的图像函数，复杂的Zernike多项式为

1.2 q-recursive法

在计算带有多个变量的多项式时q-recursive法是一种最快的算法，重复的次数不依赖于多项式的阶次。方法如下：

这里

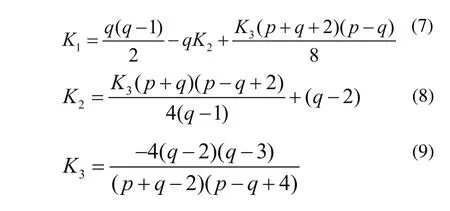
另一个指数q在式(6)的括号中以表明它是频繁变化的系数。该方法具有明显的优势，当给定一个特定的阶次p和重复系数q时，这对低阶多项式是不需要的，并不适用于其他三个方法。图1描绘了改进的方法。

图1 q-recursive算法的流程

1.3 Prata法

Prata算法用低阶多项式Rp-1,q-1(r)和Rp-2,q(r)导出一个高阶多项式Rpq(r)。当q=0,p≠q 时，用式（3）导出Rpq(r)；当p=q 时，关系式。下面给出具体的算法：

用式（3）计算

2 改进的Prata算法

有了Rpq=Rp,-q，就可以避免求多项式 ，而直接使用径向多项式Rp,0(r),p=2,4,...,pmax。现介绍改进的Prata法，如下式：

3 实验结果与分析

在此我们测试了所提出方法的性能。图2（a）作为原始图像，我们对比了q-recursive和Prata法的部分图像的亚像素边缘位置。结果如图2所示。表1列出了Prata法，q-recursive法和改进的Prata法执行时间，所有矩达到最大阶次时CPU流逝的时间。

图2 亚像素边缘的结果

实验结果表明所提出的方法在准确率上明显优于其他两种方法。这意味着所提出的方法中的边缘参数更准确。此外，还可以看出Prata法在执行时间上是最快的，因此改进的方法在速度上的改善是非常有意义的。同时可以清楚的看到改进的Prata法的阶次由降低为

表1 不同算法的时间对比

4 结论

本文提出了一种基于Zernike正交矩的亚像素边缘检测法，该方法采用了对ZMs计算的快速递归法，并修改了Prata递归法，降低了时间复杂度，由到。从实验结果看，所提出的方法更快更准确，我们用所提出的方法进行亚像素边缘定位可以得到比较满意的结果。此外，对计算目标的几何参数和使用边缘点的情况，如校准、匹配等，该新方法都是非常有效的。

[1]陈天华.数字图像处理[M].北京:清华大学出版社, 2007.

[2]ANILK.数字图像处理基础[M].北京:清华大学出版社,2006.

[3]朱虹,等.数字图像处理基础[M].北京科学出版社,2005.

[4]Tinku Acharya,Ajoy K.Ray.数字图像处理基础原理与应用[M].北京清华大学出版社,2007.

[5]J.Ye,G.K.Fu,U.P.Poudel.High-accuracy edge detection with blurred edge model,Image and Vision Computing 2005,23(5):453-467.

[6]F.Bouchara,S.Ramdani.Subpixel edge refinement using deformable models,Optical Society of America 2009,26(4): 820-832.

[7]L.Zhang,X.L.Wu.An edge-guided image interpolation algorithm via directional filtering and data fusion.IEEE Transactions on Image Processing 2006,15(8)2226-2238.

[8]T.Hermosilla,E. Bermejo,A. Balaguer,L.A.Ruiz.Non-linear fourth-order image interpolation for subpixel edge detection and localization,Image and Vision Computing 2008,26(9):1240-1248.

[9]S.O.Belkasim,M.Shridhar,M.Ahmadi.Shape recognition using zernike moments invariants,in: Proceedings of 23rd Annual Asilomar Conference on Signals Systems and Computers,1989:167-171.

[10]S.Ghosal,R.Mehrotra.Zernike moment based feature detector,in: Proceedings of International IEEE Conference on Image Processing (ICIP-94),vol.1,1994:934-938.

[11]L.Wang,G.Haealey.Using Zernike moments of the illumination and geometry invariant classification of multispectral texture, IEEE Trans. Image Process.1998,7(2):196-203.

[12]C.-W Chong,R. Paramesran.R. Mukundan.A comparative analysis of algorithms for fast computation of Zernike moments,Pattern Recognition 2003,36.731-742.

[13]A.Prata,W.V.T.Rusch.Algorithm for computation of Zernike polynomials expansion coefficients,Appl. Opt. 281989:749-754.