基于遗传算法的铁心电抗器优化设计

王延伟，刘 骥，于会凤

(哈尔滨理工大学工程电介质及其应用技术教育部重点实验室，黑龙江哈尔滨150080)

0 引言

铁心电抗器的优化设计是指在满足规定的电磁性能指标条件下，确定某一目标，运用一定的优化算法，寻求出最优的产品设计方案［1］。目前，许多算法被引入电气产品的设计领域，如随机试验法、蚁群算法、粒子群算法等［2］，但这些算法对铁心电抗器的优化设计而言，都不是很理想，不可避免地存在一定的局限性，如运算量大，求解效率低;算法本身不能确保全局寻优;算法通用性差，程序不能方便的进行移植;算法对于复杂的混合离散变量优化问题无能为力等等［3－5］。因此，在20世纪60年代中期，美国著名科学家 J．H．Holand提出了遗传算法(GA)，它是一类模拟生物进化过程与机制求解问题的自适应人工智能技术，是模拟自然界生物进化过程的一类自组织、自适应的全局优化算法。它具有很强的解决问题能力和广泛适应性。近年来，遗传算法已被成功的应用于经济管理、交通运输、工业设计等不同领域，并且在逐步地成熟和完善［6］。

1 遗传算法

1.1 遗传算法的原理

遗传算法以达尔文的生物进化论为基础，遵循适者生存的原则，合适的个体被保留，不合适的个体被淘汰。遗传算法的寻优过程是一个反复迭代过程［7］。在这种机制中，每一代中各个个体(各个设计方案)的基本特征可以通过基因转换机制被遗传到下一代中，也就是说在一个给定的代中，代表着一个群体的设计方案相互之间可以复制和交叉，并以一定的概率发生变异，交叉倾向于由群体中最为优秀的个体来承担，这种群体中相互匹配的个体的最好特性的结合使产生的子代比父代有更加优良的特性，产生好的解。如果变异后的子代性能不佳，则其在以后的选择中将被淘汰。遗传算法是一种随机搜索方法，它的搜索范围遍及整个解空间因而能以较大的概率求得全局最优解或近似最优解［8－9］。

1.2 遗传算法的特点

遗传算法对问题的求解并不依赖于所求问题的性质，不要求目标函数具有诸如连续性、导数存在和单峰等性质。与其它传统优化方法相比较，遗传算法具有的特点:遗传算法以决策变量的编码作为运算对象，而不使用参数本身;遗传算法仅使用由目标函数值变换来的适应度函数值进一步确定搜索方向和搜索范围，无需目标函数的导数值或其他辅助信息;遗传算法同时使用多个点的搜索信息，因而具有一种内在的并行性;遗传算法使用概率搜索技术，因而更具有灵活性。实践与理论证明，在一定条件下，遗传算法以概率收敛于问题的最优解。

1.3 遗传算法计算过程

如果工程优化问题为约束型，则先将其转化为无约束问题(一般采用惩罚函数法)，然后根据目标函数构造适应函数，通过反复执行选择、交叉和变异三个遗传运算过程，迭代寻优。遗传算法实施的基本步骤为:确定寻优参数，进行编码;随机生成一组原始群体;计算解群体中各个个体的目标函数值及相应的适应度值;根据解群体中各个基因链的适应值，通过选择运算形成匹配集;通过交叉、变异运算产生下一代群体;终止条件验证。如不满足终止条件，返回，进行循环迭代;如满足，程序结束。遗传算法的计算流程如图1所示。

图1 遗传算法计算流程图

1.4 遗传算子

遗传算法使用3种遗传算子，即选择、交叉、变异。

本文采用的选择算子是最基本的比例选择算子，它是一种有退还的随机选择，也叫做赌盘选择。执行过程是:先计算出群体中所有个体的适应度总和，再计算出每个个体的相对适应度大小，最后使用模拟赌盘操作，即通过产生0或1随机数来确定各个个体被选中的次数。

交叉算子中最常用、最基本的的是单点交叉，执行过程是:对群体中的个体进行两两随机配对，然后对每一对个体随机设置某一基因座之后为交叉点，再依照设定的交叉概率在其交叉点处相互互换两个个体的部分染色体，从而产生出两个新的个体，其过程如图2所示。

图2 交叉操作

变异算子是以一个小概率随机改变染色体串上的某些位，对于本文所使用的二进制编码就是相应位从1变为0，或从0变为1，变异算子能增加群体的多样性，其过程如图3所示。

图3 变异操作

2 铁心电抗器优化模型分析

铁心电抗器通过选择合适的优化设计变量、目标函数以及约束条件，可描述为

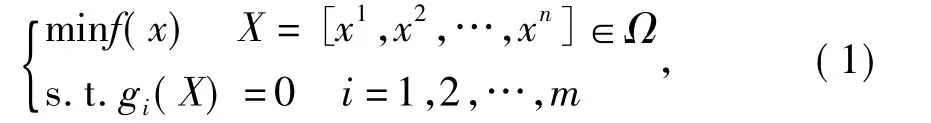
式中:X为优化变量;Ω为解空间;f(X)为目标函数;gi(X)为约束函数;m为约束函数的个数。

2.1 设计变量的选择

设计变量选择的原则是选取对电抗器的性能、目标函数和约束函数影响大，且能相应确定其他有关参量的独立设计参数作为优化设计变量。

2.2 目标函数的选择

对于电抗器的优化设计，优化的目标函数可以取电抗器的有效材料成本、损耗、温升等。本文选取电抗器的有效材料成本最低为优化目标，将性能指标条件作为约束函数处理，关系式表示为

式中:C1、C2分别为硅钢片和铜(或铝)线的单价，G1、G2分别为硅钢片和铜(或铝)线的重量;C0为与设计变量无关的固定费用。

2.3 约束条件及处理方法

约束条件主要包括电抗器的主要性能指标和实际变量上下限约束，如磁通密度、电流密度、损耗、铁芯和绕组温升等限制。

由于遗传算法属于无约束的优化方法，所以本文采用罚函数法对约束条件进行处理，将约束问题转化为无约束问题。基本思想是:针对每一个条件约束，在目标函数中增加一个相应的惩罚因子得到一个广义的目标函数:

式中Ri为惩罚因子，根据各约束的性质不同而取不同的值。

2.4 算法的实现与改进措施

标准遗传算法存在计算速度较慢、计算量较大等问题，特别是对于电磁优化这类复杂非线性问题的寻优，当搜索空间不能准确定位时，算法很容易陷入局部最优(称之为“早熟”现象)，或者浪费很长时间而得不到最优解。因此，在遗传算法的具体实现过程中，采用一些必要的技术可以使遗传算法更快、更好的收敛。

1)各惩罚项因子的确定以及惩罚函数的构造必须合适，使惩罚项的值接近实际设计值。太小时起不到惩罚作用;惩罚过度则会导致算法得不到正确的搜索信息，从而在接近最优值时不易收敛，所以需要进行多次试验以确定合理的值。

2)在遗传算法执行的过程中，同一代中各个个体的目标函数值、适应值都越来越接近，使得遗传算法的搜索速度变慢，为解决这个问题，设计了适应度函数:

式中，f(X)为适应度函数，Cmax为该代中最大的目标函数值，F(X)为待求个体的目标函数值。这样就使得个体的适应度函数值之间的差异变大，从而使遗传算法在选择操作时变得容易，加速了算法的搜索效率。

3)由于遗传算法选择的随机性，即使最优良的个体也可能在选择运算中被淘汰，或最差的个体也可能被选中，因而在遗传算法中采用保留最优模型的技术会大大改进算法的性能。一般保留当前代中前10个最优个体直接加入下一代群体中，这样在遗传过程中，就不会破坏最佳模式。

4)为了避免算法过早的收敛，在每次产生新一代群体的操作中，人为地向其中加入一定数量新的随机生成的染色体，由于这些个体遍布在整个搜索空间中，这样就增加了染色体中基因模式的种类，可以避免算法过早的收敛于局部最优解。

3 优化算例

以实际应用中典型铁心电抗器为例，比较优化前后的主要技术指标和经济性能，算例电抗器的主要技术参数如表1所示。

表1 技术参数

求解该问题的遗传算法的构造过程:

1)确定决策变量和约束条件

选取铁心直径、铁心磁通密度、线圈电流密度作为决策变量。约束条件有:损耗P0＜39．7 kW，温升T＜100 K，扁导线宽厚比为ab∈［1.4，8］，电流密度 j∈［2，2.4］，铁心磁密 B∈［1.2，1.6］，铁心直径D∈［420，460］。

2)建立优化模型

将已知量带入式(2)整理成关于决策变量的函数关系式，并作为目标函数式

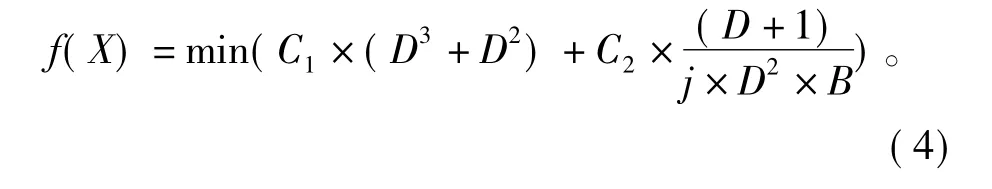
3)确定编码方法

用长度为10位的二进制编码串来分别表示三个决策变量。10位二进制编码串可以表示从0到1 023之间的1 024个不同的数，故将三个决策变量的定义域离散化为1 023个均等的区域，例如D∈［420，460］，从离散点420到460依次让它们分别对应于从0000000000(0)到1111111111(1023)之间的二进制编码。再分别将表示三个决策变量的三个10位长的二进制编码串连接在一起，组成一个30位长的二进制编码串，即构成了该问题的染色体编码方法。

4)确定解码方法

解码时需先将30位长的二进制编码串切断为三个10位长的二进制编码串，然后分别将它们转化为对应的十进制整数代码，记为y1、y2和y3，此处将铁心直径、铁心磁密、电流密度分别记为x1、x2和x3，则将yi转换为变量xi的解码公式分别为:

表2 优化结果

5)设定遗传算子

选择运算使用比例选择算子;

交叉运算使用单点交叉算子;

变异算子使用基本位变异算子。

6)确定遗传算法的运行参数

对于本例，设定遗传算法的参数如下:

群体大小:M=100。

终止代数:T=500。

交叉概率:Pc=0．6。

变异概率:Pm=0．001。

上述步骤完成了对本例遗传算法的构造，使用该方案进行优化设计后的结果如表2所示。

4 结论

1)针对传统遗传算法存在的早熟现象、收敛速度慢等缺点，提出了相应的改进措施，获得了良好的改进效果。

2)建立了铁心电抗器的优化设计模型，将遗传算法这种寻优方法加入设计中，通过对典型样例的优化可以看出，优化效果明显。

［1］路长柏．电力变压器理论与计算［M］．辽宁科学技术出版社，2007．

［2］王银年．遗传算法的研究与应用［D］．江南大学，2009．

［3］唐志国．基于遗传算法的电力变压器优化设计［J］．哈尔滨理工大学学报，2001，6(6):9 －12．

［4］裴素萍．基于改进遗传算法的变压器优化设计研究［J］．中原工学院学报，2006，17(2):52 －55．

［5］Leung Y W，Wang Y．An orthogonal genetic algorithm with quantization for global numerical optimization［J］．IEEE Trans．on Evol．Comput，2001，5(1):41 －55．

［6］樊叔维．遗传算法在电力变压器和电机全局优化设计中应用研究［J］．西安交通大学学报，1996，30(6):15－20．

［7］Hsieh C H，Chou J H，Wu Y J．Taguchi－MHGA method for optimizing Takagi－ Sugeno fuzzy gain － scheduler［J］．in Proc．2000 Automatic control conf，Taipei，Taiwan，2000:523 －528．

［8］Tsai J T，Liu T K，Chou J H．Hybid Taguchi－genetic algorithm for global numerical optimization［J］．IEEE Trans．on Evol．Comput，2004，8(4):365 －377．

［9］Vasconcelos J A，Ramirez J A，Takahashi R H．Improvements in genetic algorithms［J］．IEEE Trans．on Magnetics，2001，37(5):3414－ 3417．