发电机中间过热时间常数对电力系统频率动态过程仿真影响

李宇龙，张晏铭，李 飞，王孜航，宋杭选

(1．东北电力大学，吉林 吉林132012;2．河北邢台供电公司，河北邢台054000;3．哈尔滨电业局，黑龙江哈尔滨150030;4．黑龙江省电力科学研究院，黑龙江哈尔滨150030)

0 引言

频率是电力系统运行质量和安全情况的重要指标之一［1］。电网频率的质量，直接影响发电或者用电设备的运行安全［2］。近几十年，国内外很多大电网崩溃事故都是由于频率原因造成［3－6］。通过对发生事故时系统频率动态过程复现发现，利用原系统模型获得的频率仿真动态过程轨迹与实际事故时系统的频率动态过程轨迹存在较大的差异［7］，这说明现阶段使用的模型参数不够准确。因此，获得一组相对合理的用于电力系统频率动态过程分析的模型参数成为现阶段研究人员的主要目标之一。基于此，本文提出了校核电力系统模型参数的一种新方法，即在发电机及其调速系统模型中引入蒸汽容积效应中的过热环节，分析汽轮机中间过热时间常数(以下简称Trh)对电力系统频率仿真动态过程的影响，并通过实例验证汽轮机中间过热时间常数能够有效地修改系统频率动态仿真曲线回升斜率。

1 引入蒸汽容积效应的频率动态过程模型

与文献［8］中所采用的单机带综合负荷系统数学模型相比，本文采用的数学模型计及蒸汽容积效应，考虑了过热环节中的中间过热时间常数，这对于电力系统频率动态分析具有更普遍的意义。为了便于分析系统中各参数的关系，忽略死区及限幅作用。考虑蒸汽容积效应功－频传递函数的框图如图1所示。

图1 考虑蒸汽容积效应功－频传递函数框图

系统中频率变化与调速系统各参数变化的关系由式(1)表示。

对上式公式进行整理，可得:

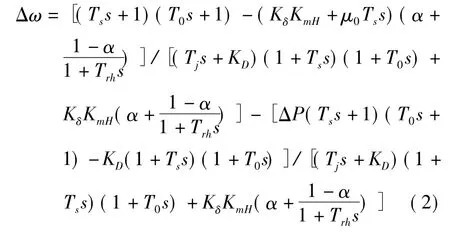
式中，PE、ωR为标幺值，Ki=1。

当系统稳定运行时，频率变化量不变，即ΔP=0时，Δω=0。所以，式(2)可进一步简化为

Ts和T0的数量级远小于Tj和Trh的数量级，忽略Ts和T0对系统频率变化量的影响，最终可获得:

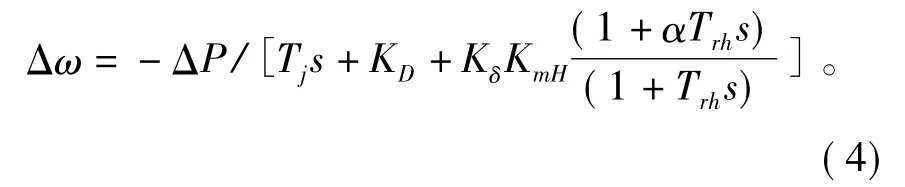
由式(4)可知，若计及蒸汽容积效应以及忽略系统中非线性环节，发电机中间过热时间常数是影响系统频率变化的主要参数之一。

2 实际系统中Trh对频率动态过程的影响

2．1 仿真工具

本研究采用中国电力科学研究院研发的《电力系统综合分析程序》(PSASP for Windows)作为仿真工具。仿真系统中调速器模型采用程序中自带的1型调速器。仿真过程中使用的数据是电力系统中采用广域量测系统获得的实测数据。

2．2 轨迹评价指标

为了便于衡量系统参数变化时，频率仿真轨迹的变化情况，现定义如下3种用于评价轨迹特征的轨迹评价指标。

1)频降最低点fmin:指发生故障后频率初始下降到最低点的值。fmin可以直接表征系统受扰程度，即:fmin越大，表明系统受扰程度越大。

2)频降斜率Kd:指频率初始变化点与频率下降过程中斜率突变点之间的斜率。Kd只与发电机惯性时间常数与功率缺额大小有关。在相同转矩的情况下，发电机惯性时间常数越大，转子转速改变越慢，频率下降时间就越长，下降的频率幅值就会越小，系统阻尼振荡的能力就越强［9］。

3)回升斜率Ke:指频率回升了20%(fmaxfmin)的点与回升了80%(fmax－fmin)的点之间的斜率。Ke表征系统一次调频能力。Ke越大，说明系统一次调频能力越强，系统可以越快的把跌落的频率值拉回到允许的范围内。反之，Ke越小则系统一次调频能力越差，系统拉升频率值得速度将会越慢。

2．3 基于实际系统研究Trh对频率动态过程影响

以东北电网实际系统模型为例，研究发电机中间过热时间常数变化时，系统频率仿真轨迹的变化规律。采用与文献［8］中相同的算例，系统中共有152台发电机，总发电功率为20 571 MW，功率脱落241 MW，占总容量的1.17%，系统负荷模型采用50%恒阻抗，50%感应电动机。

改变系统中发电机中间过热时间常数得到的系统频率动态仿真轨迹如图2所示。

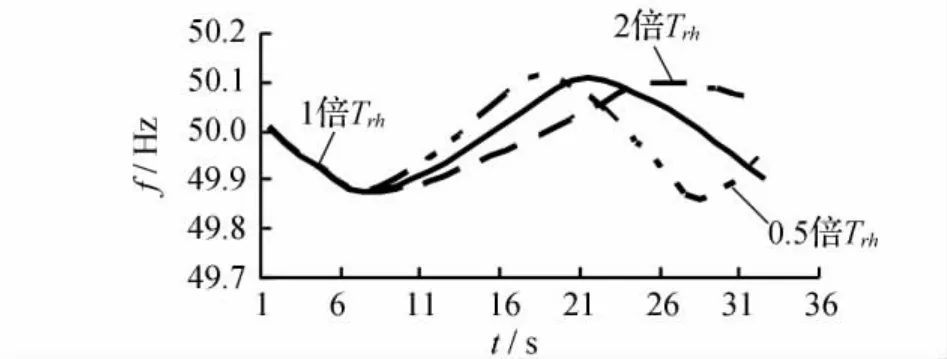
图2 发电机中间过热时间常数变化对频率仿真轨迹的影响

由图2可知，当发电机中间过热时间常数改变时，系统频率仿真曲线的最低点和回升斜率都做相应改变。发电机中间过热时间常数变化时的仿真轨迹评价指标如表1所示。

表1 发电机中间过热时间常数变化时的仿真轨迹评价指标

当Trh变化时，轨迹指标Kd不变，fmin变化很小，Ke变化较明显。据文献［9］显示频降斜率只与惯性时间常数有关，所以增加发电机中间过热时间常数并不影响频降斜率。发电机中间过热时间常数表征汽轮机出力达到额定值时所花费的时间，所以在相同出力情况的条件下，发电机中间过热时间常数越大，汽轮机出力达到额定值的时间越久，在系统频率稳态值不变的前提下，增大发电机中间过热时间常数，系统最终稳定所需要的时间就越长，仿真频率的回升斜率就越小;发电机中间过热时间常数越大，汽轮机出力达到额定值的时间越久，则单位时间内汽轮机出力将减少，用于抑制频率曲线下降的能力将会降低，所以频率最低点将会下降。

通过以上分析可知，发电机中间过热时间常数的变化只对频率仿真曲线回升斜率有较明显的影响，所以，发电机中间过热时间常数具有很优秀的调节频率仿真曲线回升斜率的能力。在拟合频率动态仿真曲线时可以充分利用发电机中间过热时间常数这一特性。

3 算例分析

文献［8］详细地分析了惯性时间常数、调差系数、死区对系统频率仿真曲线的影响。其中，惯性时间常数用于调整频降斜率，调差系数用于调整仿真频率轨迹的回升斜率，死区是用来调节频率仿真曲线最低点。调差系数变化与系统频率仿真轨迹变化的对应关系，如图3所示。

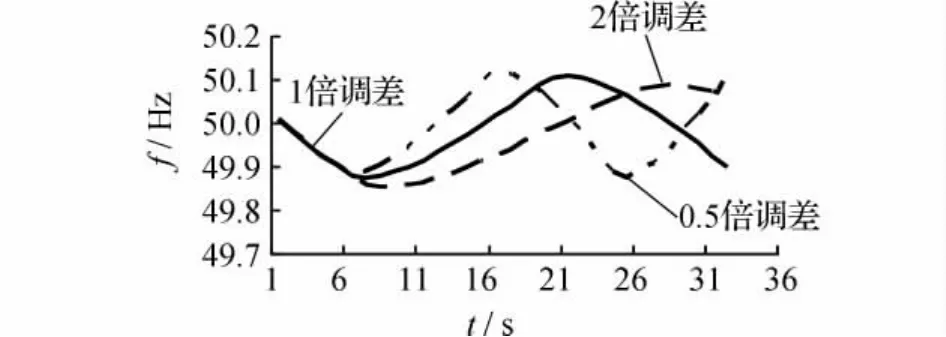
图3 调差系数变化对频率仿真轨迹的影响

从图3中可知，当调差系数改变时，系统频率仿真曲线会发生相应的变化，其中，仿真频率曲线最低点以及回升斜率的变化较明显。调差系数变化时的仿真轨迹评价指标如表2所示。

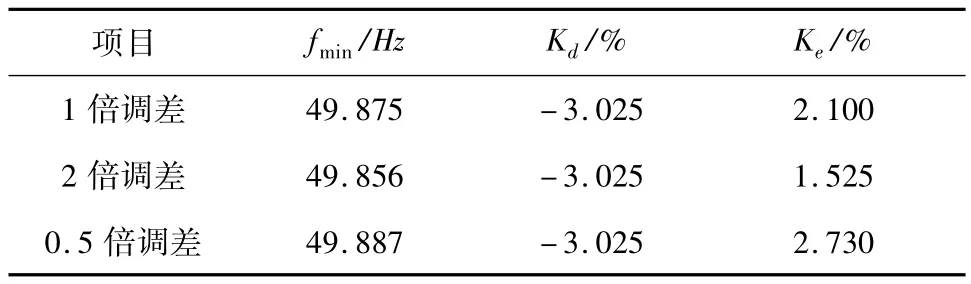
表2 调差系数变化时的仿真轨迹评价指标

比较表1和表2中各轨迹指标量，发现发电机中间过热时间常数和调差系数做同样倍数变化时，两者对于系统频率仿真曲线回升斜率的影响比较接近;但若考虑其对于系统最低点的影响，发电机中间过热时间常数的影响明显小于调差系数的影响。发电机中间过热时间常数更适合作为调整频率仿真轨迹回升斜率的参数。

以汽轮机中间过热时间常数代替调差系数，重新制定参数调整方案。经仿真计算后，只需调整惯性时间常数为原值的1.5倍，发电机中间过热时间常数为原来的5倍，即可获得与实际轨迹充分接近的频率动态仿真轨迹，校正参数后的仿真系统的频率动态过程如图4所示。

图4 校正参数后的仿真系统的频率动态过程

实测曲线，基于原始参数的频率仿真曲线以及基于修改后参数的频率仿真曲线的具体轨迹评价指标如表3所示。

表3 各曲线轨迹评价指标

通过表3可知，修改发电机中间过热时间常数同样可以使频率动态仿真轨迹逼近于实际轨迹。与文献［8］中采用的方法相比，由于惯性时间常数与发电机中间过热时间常数变化对最低点影响都很小，若基于原始参数频率仿真曲线的最低值与实测相同，则在调整参数过程中可以忽略系统仿真轨迹最低点的调整。

4 结论

在电力系统频率动态仿真过程中若引入蒸汽容积效应环节，则必须考虑发电机中间过热时间常数。发电机中间过热时间常数的改变对频率仿真轨迹的频降斜率无影响、对最低点影响很小、对回升斜率影响较大。与调差系数相比，在调整同等回升斜率的前提下，发电机中间过热时间常数对于频率仿真轨迹最低点的影响更小。这说明在引入蒸汽容积效应环节的前提下，发电机中间过热时间常数更加适宜用来调整频率仿真轨迹的回升斜率。

［1］蔡邠．电力系统频率［M］．北京:中国电力出版社，1981．

［2］陈珩．电力系统稳态分析［M］．北京:中国电力出版社，1985．

［3］陈向宜，陈允平，李春燕，等．构建大电网安全防御体系－欧洲大停电事故的分析与思考［J］．电力系统自动化，2007，31(1):4－8．

［4］印永华，郭剑波，赵建军，等．美加“8．14”大停电事故初步分析以及应吸取的教训［J］．电网技术，2003，27(10):8 －11，16．

［5］胡学浩．美加联合电网大面积停电事故的反思和启示［J］．电网技术，2003，27(9):2 －6．

［6］薛禹胜．综合防御由偶然故障演化为电力灾难—北美“8．14”大停电的警示［J］．电力系统自动化，2003，27(18):1 －5，37．

［7］唐磊．汽轮发电机组调速系统动态模型参数辨识与仿真研究［D］．武汉:华中科技大学，2009:1－76．

［8］刘洪波，穆钢，徐兴伟，等．使功－频过程仿真轨迹逼近实测轨迹的模型参数调整［J］．电网技术，2006，30(18):20 －24．

［9］刘少华．基于频率特性的低频减载方案的校核研究［D］．吉林:东北电力大学，2010．