兆瓦级风力发电机在极限工况下流体场与温度场数值分析

葛云中

(中国人民解放军96215部队，广西 柳州545616)

0 引言

近年来，风力发电产业迅速发展，大容量的风力发电机组不断投入运行。但是，随着发电机单机容量的增加，电机温升也大幅度地提高，影响电机的安全运行和使用寿命。目前，国内外研究风力发电机温度场和流体场的相对较少，特别是对高海拔恶劣环境条件下运行的风力发电机温度场和流体场的研究甚少。因此，本文从中国高原地区风力发电现状进行分析，研究风力发电机在海拔4 km地区极限工况下流体流变特性和电机热特性。

1 数学模型

电机冷却系统内流体流动满足质量守恒、动量守恒和能量守恒定律［1］。

1.1 k－ε湍流模型

对于湍流则采用标准的k－ε湍流模型，可统一表达为以下形式:

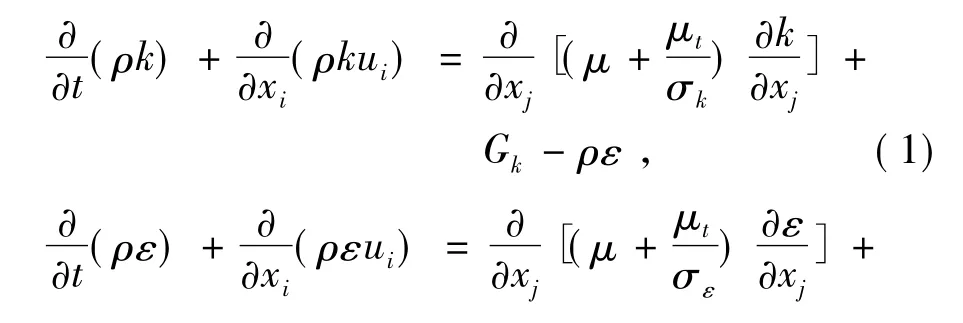
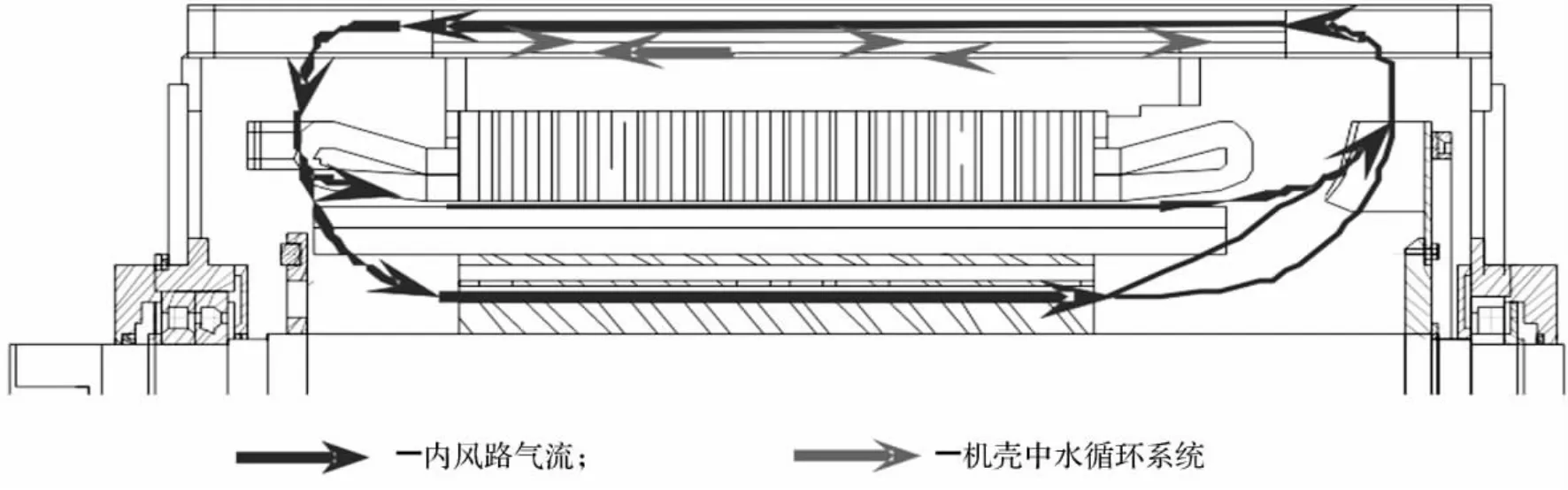
图1 发电机冷却系统

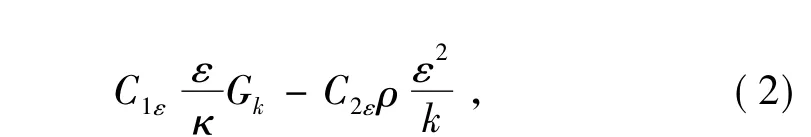
1.2 三维热传导方程

在直角坐标系下，三维热传导方程为

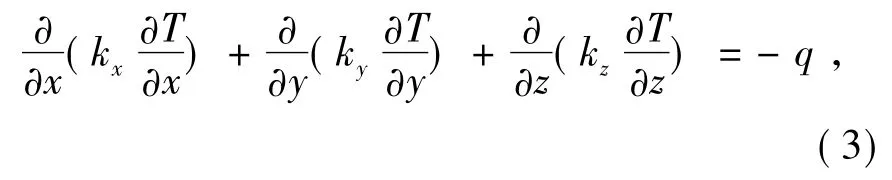
式中:T为固体待求温度，oC;kx、ky、kz分别代表x、y、z方向的导热系数，W/(m·K);q为内部热源密度，W/m3。

2 求解域模型确定

2.1 电机冷却系统结构

本文以一台双馈水冷风力发电机为研究对象，该发电机具有内外两路冷却系统。内冷却系统，即空气由设在电机端部的风扇强迫通风实现封闭式冷却。外冷却系统，发电机机壳内设有水循环系统，冷却水经过与一次冷却的热空气进行能量传递，将发电机运行时产生的热量带到外部。发电机冷却系统如图1所示。

2.2 基本假设

根据电机结构、传热和冷却系统的特点，作如下假设［2-5］:

1)将电机上层绕组和下层绕组分别按整体加以考虑。

2)电机各部件紧密接触，所有绝缘材料性质相同。

3)不考虑风扇实际存在，端部绕组用直线段取代。

4)由于电机中流体的雷诺数很大(Re＞2 300)，属于紊流，因此采用紊流模型对电机内流场进行求解。

2.3 计算区域

根据电机基本数据，在基本假设下，建立电机圆周方向1/8个区域为求解模型，求解域物理模型如图2所示。电机的基本参数如表1所示。

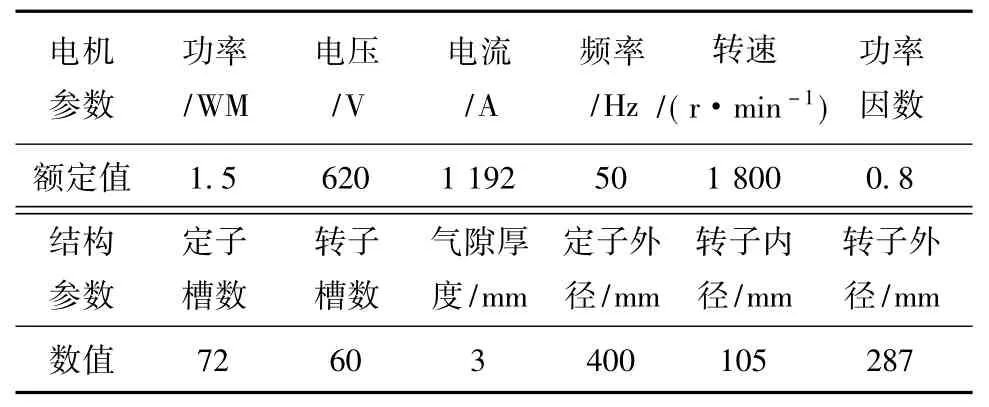
表1 电机的基本参数

图2 求解域物理模型

2.4 边界条件

边界条件为:

1)入口1及入口2为速度入口。

2)出口1及入口2为压力出口。

3)发电机机壳外圆及转子内圆为散热面，散热系数的确定有文献给定［6］。

4)冷却介质的特性由发电机所处的具体海拔高度确定。

3 流体特性分析

采用有限体积法对电机内三维流体场和温度场进行耦合求解，得出电机内流体速度分布。

3.1 空气速度分布

图3为电机内空气速度分布。

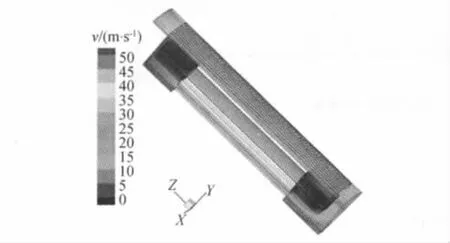
图3 空气速度分布图

通过对图3流体分布以及计算数值结果分析，空气在转子通风孔的速度最大，为49.96 m/s。电机端部空气流通空间大，流动速度相对较小，在流通空间变化大的区域速度变化较大，并有涡流产生。

3.2 水速度分布

图4为水冷系统中冷却水的流线分布。

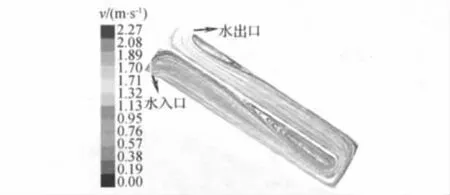
图4 水流场流线图

从图4可以看出:在求解域外冷却系统中冷却水在冷却过程中速度较低，其数值为2.27 m/s。在实际的电机中，电机的出入口均为一个，即在电机整个外冷却系统中水的最大速度也为2.27 m/s。

4 温升特性分析

4.1 电机整体温升分布

图5为风力发电机在高原极限工况下温升分布。

图5 电机温升分布图

从图5可见，电机风扇端定子股线受散热条件的影响，定子端部股线温升明显高于电机的其它部分，最高温升达100.9 K。其次是转子区域温升，最高温升为100.1 K。由于转子股线和铁心紧密接触，因此，相对应的转子铁心温升也较高。另外，空气在电机内流动到风扇端的过程中温度不断变高，所以，电机风扇端的温升明显高于非风扇端的温升。

由于液体工质的密度与比热容都远远大于气体工质，带走热量能力强，因此，机壳以及定子区域温升低于转子区域。

4.2 转子温升分布

图6为转子最热区域轴向截面温升分布图，图7为转子股线沿轴向长度温升分布图。

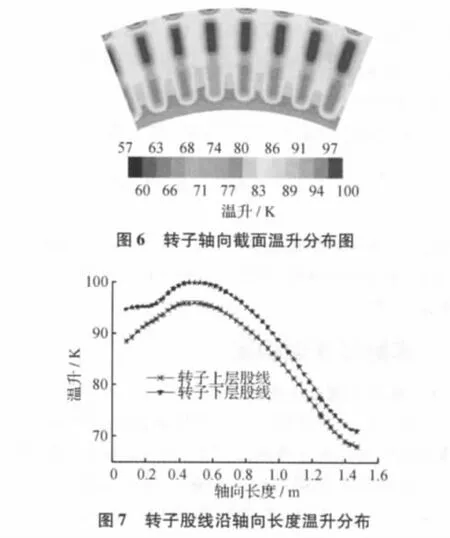
从图6、图7中可以看到:

1)转子槽内温升高于其它各个部分，槽口、齿根和轭部温升较低。

2)平面内的温升最高点位于槽中心线上，沿着两侧绝缘层温升快速下降，在铁心位置趋于稳定，并且沿着周向呈对称分布。

3)股线和铁心紧密接触，转子股线的最热位置与铁心的最热位置相对应。

4)槽内上层股线温升高于下层股线，除在风扇端外，双层绕组变化规律基本一致，温升差约为2.9～4.1 K。转子端部股线产生的热量主要由端部流动的空气带走，上层绕组在背风区，散热较下层绕组困难，上层绕组温升下降慢，上下层绕组温升相差最大为6.2 K。

4.5 水温升分布

图8为机壳中水循环系统的温升分布。

图8 水温升分布图

从图8可以看出:在求解域水冷系统中水的温升较低，最大温升为1.8 K，出水口平均温升为1.22 K。

通过对图4和图8的对比分析，水循环系统内速度分布与温升分布是相对应的。在涡流区和水流动较慢的区域水的温升较高;而水流通畅的区域水的温升低。

5 结论

通过上述建立的风力发电机数学模型与实际使用风力发电机的性能分析计算对比，其结果为:

1)平原地区工作的发电机的性能与本次实验的发电机的性能数值误差为4.24%，满足运行要求。

2)在高原极限下运行时，电机最高温升为100.9 K，远小于F级绝缘条件所允许的最高温升。由此表明电机适应高原环境风速变化，在极限工况下，可以安全、可靠运行。

3)电机气隙热阻大，径向温差大，整体温升分布呈现出了两个温差较为明显的区域:转子温升区和定子温升区。

［1］周俊杰，徐国权，张华俊.FLUENT工程技术与实例分析［M］.北京:中国水利水电出版社，2010:14-17.

［2］吴德义.大型空冷汽轮发电机通风结构中气体运动流场的合理建模［J］.大电机技术，2005(6):8-10.

［3］丁树业，李伟力，靳慧勇，等.发电机内部冷却气流状态对定子温度场的影响［J］.中国电机工程学报，2006，26(3):131-135.

［4］KOMEZA K，LóPEZ-FERNáNDEZ X M，LEFIK M.Computer modelling of 3D transient thermal field coupled with electromagnetic field in three-phase inductionmotor on load［J］.The International Journal for Computation and Mathematics in Electrical＆Electronic Engineering，2010，29(4):974-983.

［5］温志伟，顾国彪，王海峰.浸润式与强迫内冷结合的蒸发冷却汽轮发电机定子三维温度场计算［J］.中国电机工程学报，2006，26(23):133-138.

［6］丁舜年.大型电机的发热与冷却［M］.北京:科学出版社，1992.