带有工件实际加工时间上界的调度问题研究

虞先玉， 游 运， 温荣生

(东华理工大学理学院，江西 南昌 330000)

在很多的调度问题研究中，工件的加工时间都被认为是在工件加工过程中是保持不变的(Graham et al.，1979;程朋根等，2002;周珏等，2009)。在很多实际情况下，工件的实际加工时间会因为生产机器老化、生产人员不断积累生产经验等因素影响而变化。在老化因素主导的环境中，工件在生产序列中越靠后，工件的实际加工时间就越长;在学习因素主导的环境中，工件在生产序列中越靠后，工件的实际加工时间就越少。

关于老化和学习影响的调度研究在过去十年里受到越来越多学者们的关注。其中大多数研究假设工件实际加工时间服从特殊的老化或学习函数模型。在这些研究中(如 Biskup，2004;Kuo，2008;Yang et al.，2010a，2010b;Zhao，2010)使用了指数函数模型;另外一些研究(Cheng，2000;Bachman，2004;Wang，2006)考虑了不同形式的线性模型。一些学者则给出了线性函数和指数函数组合的模型(Lee，2004;Cheng et al.，2008;Wang，2007a;Wang，2007b;Cheng，2010)。Yin et al.(2009)研究了一类位置依赖的学习函数模型，其中涵盖了很多已有的相关研究成果。Lai et al.(2011)提出了一类以已加工工件的加工时间和加工位置为变量的一般性学习函数模型。Yin et al.(2009)和Lai et al.(2011)研究的函数工件实际加工时间模型仍然部分包含有加法及乘法运算。只有少数的研究(Mosheiov et al.，2003;Mosheiov，2011)包含没有任何特殊结构的工件加工时间函数模型。

在实际的车间生产过程中，生产机器往往会受到磨损或零件老化，需要定期或不定期的机器维护以防止机器持续不健康运行或损坏。因此，很多研究(Ji et al.，2006;Kuo et al.，2008;Gawiejnowicz et al.，2010;Yang et al.，2010;Zhao et al.，2010)报道了带有机器维护的调度问题。另外，在实际的食品加工或陶瓷烧制等加工过程中，每件产品往往会有一个不允许超过实际加工时间上界。如果超过时间上界，加工完的产品就会有瑕疵或缺陷。带有老化或学习时间限制的调度问题近年受到了学者们的关注。Inderfurth et al.(2006)研究了一类旧产品恢复再制造的调度问题，引入了一个给定的产品老化(或恶化)时间限制;如果某个产品没有超过这个老化时间限制，这个产品就可以回收再利用和制造新产品，否则产品则不能用于再制造。Gawiejnowicz(2007)研究了一类每个工件带有准备时间和生产期限的单机调度问题。

目前很少有同时考虑加工时间上界、一般性工件加工时间函数和机器维护的调度研究工作。由此启发，本文将分别研究带有工件实际加工时间上界限制的单机调度问题和平行机调度问题。对于单机调度问题，考虑了机器维护，研究的目标函数是最小化工件总完工时间;对于平行机调度问题，分别考虑了工件的实际加工时间函数有单调性和没有单调性两种情形，研究的目标函数为最小化机器的总负荷。

1 问题构建和符号说明

基本的模型和所研究问题表述如下:

对于单机调度问题，假设在生产车间中有n个工件J1，J2，……，Jn需要被安排在机器上生产。工件Jj(j=1，2，…，n)的正常加工时间和完工时刻分别记为pj和Cj。假设每次机器维护的时间为t。当机器进行维护时，假设机器是不运转的，进而生产过程是停止的。经过每次机器维护，机器就恢复到初始状态。机器维护频率记为m，不等式m≤μ(μ往往远小于工件个数n)，则表示机器维护次数不能超过次维护。

当一个可行的排序调度中进行了k(即m=k)次机器维护时，则所有机器上的工件就被次机器维护划分成k+1个工件组。令Mi表示第i(1≤I≤k)次维护，Gi表示第i(1≤i≤k+1)个工件组。进而，整个调度可以表示为[G1，M1，G2，M2…，Mk，Gk+1]。当工件Jj被安置在第i个工件组的第r个位置上时，其实际加工时间为:

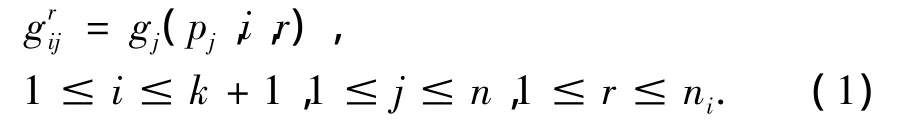
由于机器在维护后就恢复到初始状态，工件实际加工时间只同工件的正常加工时间和工件在每个组中排序位置有关，与工件组序号无关。在不引起混淆的情形下，令

当工件被排在工件组的第一个位置，位置依赖影响没有发生，因此得到:

设工件Jj的实际加工时间上界为Uj。对于每一个可行的调度，工件Jj的实际加工时间必须不大于Uj(1≤j≤n)工件的初始加工时间必须满足pj≤Uj(1≤j≤n)，否则所研究的调度问题就已经没有可行的调度方案。

对于所要研究的平行机问题，假设在生产车间中有n个工件J1，J2，…，Jn需要被安排在平行机器上生产加工。所有的工件在零时刻开始都是可用于调度的。同单机问题一样，工件Jj(j=1，2，…，n)的正常加工时间和完工时刻分别记为pj和Cj。当工件Jj安置在机器i上第r个位置上时，其实际加工时间为:

因为平行机的调度中机器是同规格的，所以同一个工件在不同机器的相同排序位置上的实际加工时间是相同的。在不引起混淆的情形下，令

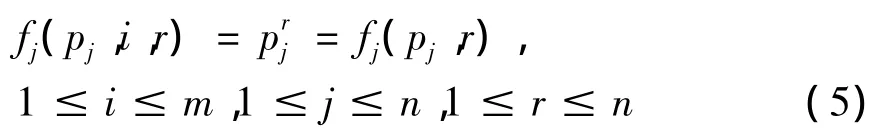
同(3)式类似，当工件排在机器第一个位置时，其实际加工时间为:

一些研究(Graham et al.，1979;Agnetis et al.，2004 和 Kuo et al.，2008)中所使用的三阶段方法表示所研究的问题。

首先考虑的是一类单机调度问题:其优化目标为总完工时刻最小化的问题;工件实际加工时间有相应的上界，机器维护的次数有上界。把这类调度问题表示为:

相似地，带有一般性位置依赖影响的最小化机器总负荷的平行机调度问题可以表示为:

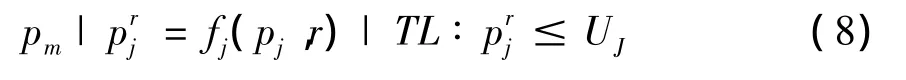
2 问题的相关性质与求解算法

2.1 单机问题

由于prj≤Uj，构建新的工件的实际加工时间函数:

证明: 这里利用类似于Mosheiov(2012)中处理一般性位置依赖的平行机调度问题的方法处理1首先，分别给出各种维护次数下的n个工件的各种分组。当维护次数m=μ时，工件被机器维护分隔成μ+1组，由Ji et al.(2010)可知，这时工件分组过程的计算复杂度为O(nμ)。显然满足维护次数约束的机器维护次数可能为 0，1，2，…，μ。因此，全部的分组过程的计算复杂度为:O(n1)+O(n2)+… +O(nμ)=O(nμ)。

接着，对于每一个工件分组，确定各个工件组内工件的排序，使目标函数∑Cj最小化。不失一般性，对于一个工件分组(n1，n2，…，nm+1)，可以把问题1转化为如下标准的任务分派问题:

其中当工件j被安排在第i组的第r个位置时xijr=1，否则xijr=0。众所周知，标准的任务分派问题得到最优调度的复杂度为O(n3)。

对于每一个工件分组都得出一个最优调度，比较所有的分组的最优调度目标函数值，得到最小的目标函数值及其对应的调度。若所得到目标函数值小于A1，则得到满足条件grj≤Uj的最优目标函数值及其对应的最优调度;否则，则不存在满足条件的调度。此过程的计算复杂度为O(nμ)。

综合以上分析，整个求解过程的计算复杂度为:O(nμ)× O(n3)+O(nμ)=O(nμ+3)证毕。

算法1

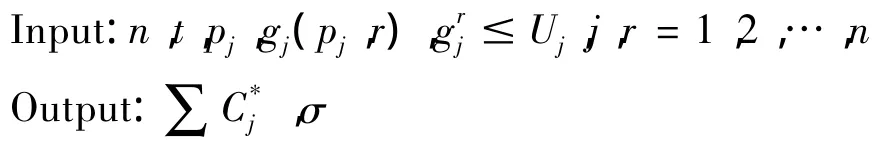
2.2 平行机问题

对于平行机问题pm|prj=fj(pj，r)|TL ∶prj≤Uj，令 J[l，r]及 p[l，r]、C[l，r]分别表示排在第 l台机器第r个位置的工件及其正常加工时间、实际加工时间、完工时刻。

对于平行机问题pm|prj=fj(pj，r)|TL:prj≤Uj，考虑到 prj≤Uj，构建新的工件的实际加工时间函数:

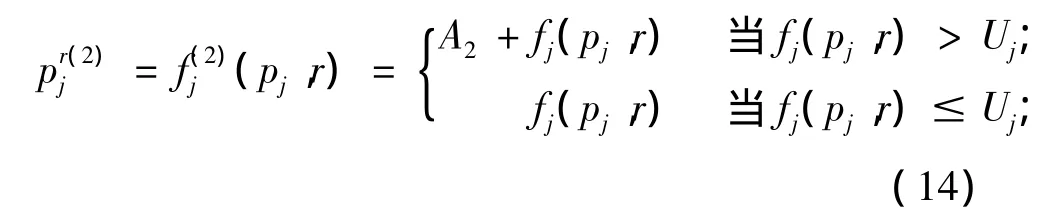
证明:把每一台机器上的工件看作一个工件组，列出n个工件的分成m组的各种分组情形。由研究Ji et al.(2010)可知，此时工件分组过程的计算复杂度为 O(nm－1)。

对于每一个工件分组，确定各个工件组内工件的排序，使目标函数TL最小化。不失一般性，对于一个工件分组(n1，n2，…，nm)，可以把问题 pm|prj=fj(pj，r)|TL:prj≤Uj转化为如下标准的任务分派问题:

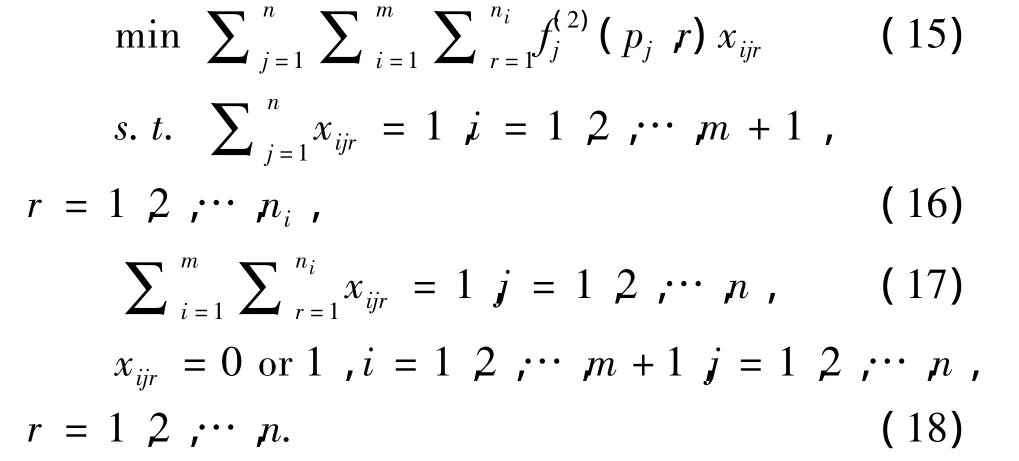
其中当工件j被安排在第i组的第r个位置时xijr=1，否则xijr=0。这一步任务分派问题寻优操作的复杂度为O(n3)。

比较所有的分组的最优调度目标函数值，得到最小的目标函数值及其对应的调度。若所得到目标函数值小于A2，则得到满足条件prj≤Uj的最优目标函数值及其对应的最优调度;否则，则不存在满足条件prj≤Uj的调度，此过程的计算复杂度为O(nm－1)。

综合以上分析，整个求解过程的计算复杂度为:O(nm－1)× O(n3)+O(nm－1)=O(nm+2)。证毕。

根据以上证明过程，给出求解问题pm|prj=fj(pj，r)|TL:prj≤Uj的算法2:

算法2

计算出 f(j2)(pj，r)

列出n个工件分成m组所有组合情形;

记所有工件分组数目为N′;

处理任务分派问题(1 5)～(1 8);

计算出T L(k);

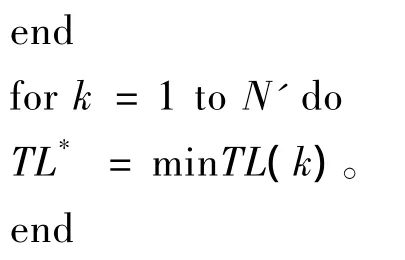
在工件实际加工时间关于排序位置而单调递增的条件下，分析平行机问题pm|prj=fj(pj，r)|TL:prj≤Uj的求解复杂度。

Kuo et al.(2008)提出的带有机器维护的单机调度问题的组平衡原则。在问题pm|prj=fj(pj，r)|TL:prj≤Uj中，一共有m台机器可供使用。则在每一个可行的调度中，工件被分成m个工件组，问题pm|prj=fj(pj，r)|TL:prj≤Uj对应的组平衡原则可以表述如下:n个工件被分成m个工件组G1，…，Gi，…，Gm;记分组Gi(1≤i≤m)的工件个数为ni(1≤i≤ m)，则满足[n/m]≤ ni≤[n/m]+1。

引理1 对于问题pm|prj=fj(pj，r)|TL ∶prj≤Uj，如果工件实际加工时间关于排序位置而单调递增，必存在其最优调度满足分组平衡原则。

证明: 由于工件实际加工时间fj(pj，r)关于排序位置而单调递增，运用类似于 Zhao et al.(2010)分析方法，容易证明存在问题pm|prj=fj(pj，r)|TL:prj≤Uj的最优调度满足分组平衡原则。证毕。

定理3 对于问题pm|prj=fj(pj，r)|TL:prj≤Uj，如果工件实际加工时间关于排序位置而单调递增，问题求解的计算复杂度为O(n3)。

证明:由引理1，当工件实际加工时间关于排序位置而单调递增时，其最优调度必满足分组平衡原则。由于考虑的平行机，各机器认为是无差异的。因此设l=n－n×[n/m](l可能为0)，令 n1=n2=… =nl= [n/m]+1，nl+1= … =nm=[n/m]。由此，得到最优调度的工件分组，问题pm|prj=fj(pj，r)|TL:prj≤Uj可以转化为任务分派问题(15)～(18)，其求解的计算复杂度为O(n3)。证毕。

由定理3的证明过程，给出工件实际加工时间关于排序位置而单调递增条件下，问题pm|prj=fj(pj，r)|TL:prj≤Uj的求解算法3。

算法3

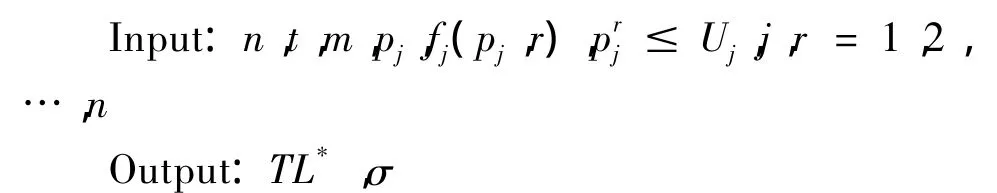
计算出 f(j2)(pj，r)

按照分组平衡原则把n个工件分成m组;

处理任务分派问题(15)～(18);

计算出最优的总负荷TL*。

3 结论

研究了带有工件实际加工时间上界的一般性位置依赖的单机调度和平行机调度决策问题。对于目标函数为总完工时刻且机器维护次数有上界μ的单机调度问题，分析得出求解问题的计算复杂度为O(nμ+3)，并给出了求解算法原码。对于目标函数为机器总负荷的台平行机的调度问题，分析得到求解问题的计算复杂度为O(nm+2)，并根据计算复杂度的分析过程，给出了求解算法原码;当工件实际加工时间关于排序位置单调递增时，则证明了求解研究平行机调度问题的计算复杂度可以下降到O(n3)。

程朋根，熊助国，韩丽华.2002.基于GPS技术的大型结构物健康动态监测[J].华东地质学院学报，25(4):324-328.

周珏，程朋根，李静.2009.基于MS4W和GPRS/GSM的车辆综合监控系统设计与实现[J].东华理工大学学报:自然科学版，32(2):177-180.

Agnetis A，Mirchandani P B，Pacciarelli D，Pacifici A.2004.Scheduling problems with two competing agents[J].Operations Research，52:229-242.

Bachman A，Janiak A.2004.Scheduling jobs with position-dependent processing times[J].Journal of the Operational Research Society，55:257-264.

Biskup D.1999.Single-machine scheduling with learning considerations[J].European Journal of Operational Research，115:173-178.

Cheng T C E，Lee W C.2010.Scheduling problems with deteriorating jobs and learning effects including proportional setup times[J].Computers＆ Industrial Engineering，58(2):326-331.

Cheng T C E，Wu C C，Lee W C.2008.Some scheduling problems with deteriorating jobs and learning effects[J].Computers and Industrial Engineering，54:972-982.

Cheng T C E，Wang G.2000.Single machine scheduling with learning effect considerations[J].Annals of Operations Research，98:273-290.

Gawiejnowicz S.2007.Scheduling deteriorating jobs subject to job or machine availability constraints[J].European Journal of Operational Research，180(1):472-478.

Graham R L，Lawler E L，Lenstra J K，et al.1979.Optimization and approximation in deterministic sequencing and scheduling:A survey[J].Annals of Discrete Mathematics，5:287-326.

Inderfurth K，Janiak A，Kovalyov M Y，Werner F.2006 Batching work and rework processes with limited deterioration of reworkables[J].Computers＆ Industrial Engineering，33:1595-1605.

Ji M，Cheng T C E.2010.Scheduling with job dependent learning effects and multiple rate-modifying activities[J].Information Processing Letters，110:460-463.

Kuo W，Yang D L.2008.Minimizing the makespan in a single machine scheduling problem with the cyclic process of an aging effect[J].Journal of the Operational Research Society，59:416-420.

Lai P J，Lee W C.2011.Single-machine scheduling with general sumof-processing-time-based and position-based learning effects[J].O-MEGA-The International Journal of Management Science，39(5):467-471.

Lee W C.2004.A note on deteriorating jobs and learning in single-machine scheduling problems[J].International Journal of Business and Economics，3:83-89.

Mosheiov G，Sidney J.2003.Scheduling with general job-dependent learning curves[J].European Journal of Operational Research，147:665-670.

Mosheiov G.2011.Proportionate flowshops with general position-dependent processing times[J].Information Processing Letters，111(4):174-177.

Mosheiov G.2012.A note:Multi-machine scheduling with general position-based deterioration to minimize total load[J].International Journal of Production Economics，135(1):523-525.

Wang J B，Xia Z Q.2006.Flow shop scheduling with deteriorating jobs under dominating machines[J].OMEGA-The International Journal of Management Science，34(4):327-336.

Wang J B.2007a.Single-machine scheduling problems with the effects of learning and deterioration[J].OMEGA-The International Journal of Management Science，35(4):397-402.

Wang，J B，Cheng T C E.2007b.Scheduling problems with the effects of deterioration and learning[J].Asia-Pacific Journal of Operational Research，24:1-17.

Yang S J，Yang D L，Cheng T C E.2010a.Single-machine due-window assignment and scheduling with job-dependent aging effects and deteriorating maintenance[J].Computers＆ Operations Research，37:1510-1514.

Yang S J，Yang D L.2010b.Minimizing the makespan on single-machine scheduling with aging effect and variable maintenance activities[J].OMEGA-The International Journal of Management Science，38:528-533.

Yin Y Q，Xu D H，Sun K B，et al.2009.Some scheduling problems with general position-dependent and time-dependent learning effects[J].Information Science，179:2416-2425.

Zhao C L，Tang H Y.2010.Single machine scheduling with general job-dependent aging effect and maintenance activities to minimize makespan.Applied Mathematical Modelling[J].34:837-841.