一种抗干扰的改进型Smith预估控制器

夏 洪

(东华理工大学机械与电子工程学院，江西 南昌 330013)

化工、炼油和制药等生产过程中的大滞后系统是很难控制的系统。Smith预估控制方法是用于大滞后系统控制的有效方法之一，然而基本型Smith预估控制方法是建立在精确数学模型基础上的。预估器根据对象的传递函数Gp(s)和滞后时间τ来计算，设计时必须精确辨识对象的Gp(s)和τ。它对误差很敏感，当辨识Gp(s)和τ有一定误差时，则控制性能较差。人们提出了多种改进型Smith控制方法，但是这些方法普遍存在抗干扰能力不够好的问题(赵东亚等，2010)。改进Smith控制系统的容差性能和抗干扰性能，是它在工程中应用的关键。

辨识被控对象的模型和滞后时间较为困难。一些文献介绍了各种辨识方法，包括各种神经网络法(韩冰等，2010;谢成清等，2011)。这类方法辨识速度较慢，且精度受对象不确定性的影响。

刘文定等(2009)介绍了一种改进型Smith预估控制器，对模型失配有补偿作用(以下简称为失配补偿Smith控制器)。它容许预估器和对象模型有一定的误差，设计时不需要知道对象的纯滞后时间;因此对辨识的要求比较低。其缺点是:抗随机干扰的性能不好。因此它难以在生产过程中广泛使用。

一些学者为了提高Smith控制器的抗干扰性能做出了努力(杨平等，2010)。例如:Uma等(2010)，姜克君等(2011)研究了Smith控制系统抗扰性能的改善方法。然而这些改进型Smith控制方法在抑制随机振荡型干扰方面还是不够理想的。

本文提出一种改进型的Smith预估控制器。它在失配补偿Smith控制器基础上，增加了一套抗干扰补偿装置，可以大大提高抗干扰能力，从而使系统容易得到满意的控制性能。本文将对该控制系统作仿真研究，以验证它的控制性能。

1 改进型Smith预估控制系统

失配补偿Smith控制系统的框图如图1。其中:τ为被控对象的滞后时间;Gp(s)为被控对象的去掉滞后的传递函数;Ge(s)为对Gp(s)的辨识结果，Ge(s)和Gp(s)之间有一定的误差，Ge(s)可以不含滞后;X(s)为系统的期望值，即系统的输入;Y(s)为控制系统的输出;N(s)为系统受到的负载干扰;Gc(s)为主控制器，一般是PID控制器;Gf(s)为反馈补偿器。可采用PI控制器;GN(s)为干扰通道的传递函数。

主控制器Gc(s)的输出u经过Ge(s)后，产生信号v，v通常不等于系统输出Y。计算出Y和v的误差后，把这项误差输给Gf(s)，经Gf(s)反馈到环节Ge(s)，再把信号v反馈到系统的输入端。这种反馈起到了补偿作用，可以补偿Ge(s)和对象模型的失配误差，从而改善系统的性能。

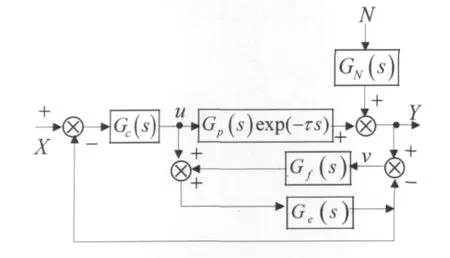
图1 失配补偿Smith控制系统的框图Fig.1 Diagram of smith control system with compensator for mismatch

从图1可知，系统中需要用器件实现的有主控制器Gc(s)、反馈补偿器Gf(s)和补偿器Ge(s)，它们都不含有对象的滞后时间τ，因此不需要辨识τ，只需要辨识Gp(s)，而且容许有一定的辨识误差。本文用仿真结果证明，这种控制系统容错性好，在没有受到较大干扰时，控制性能较好。但是受到较大干扰时，则控制性能明显变差。

2 有干扰补偿的改进型Smith预估控制器

本文提出一种有抗干扰补偿的改进型Smith预估控制系统。它是在图1所示系统上增加了干扰补偿装置Wc和Wg。选取合适的Wc和Wg，可以大大提高系统的抗干扰能力。其框图如图2所示。

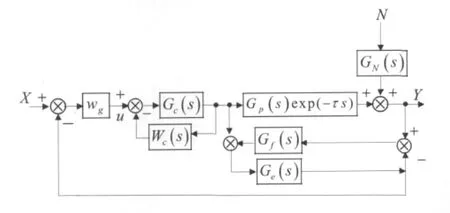
图2 有抗干扰补偿的改进型Smith控制系统的框图Fig.2 Diagram of improved Smith control system with anti－interference compensator

一般选取Wc(s)为a/(cs+d)形式，其中a、c、d为常数，用试凑法确定。Wg(s)可以是一阶环节，其参数也由试凑法确定。

本文通过simulink仿真来说明其抗干扰效果。

3 计算机仿真实例

选取某炼油厂的一个加热炉的温度控制系统作为研究对象。被控对象的传递函数为:

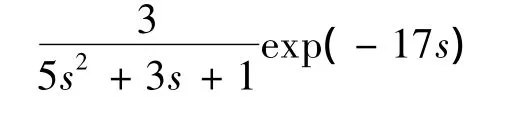
对Gp(s)的辨识结果Ge(s)为Ge(s)和Gp(s)exp(–17s)之差就是辨识误差。

系统的参考输入为幅值为5的阶跃函数。

图2中，系统受到的干扰为对象的质量变化和结构参数随机变化引起的干扰，所以在控制框图中干扰在对象之后。通常它是阶跃干扰和随机振荡干扰的叠加。仿真时取阶跃干扰幅值为11.5，随机干扰最大值为6，最小值为–6。干扰的传递函数为:这个干扰的作用是比较强的。

为使系统无静差，选取主控制器为PI(比例积分)控制器。用凑试法整定该控制器的PI参数，得:比例系数为 Kp=0.011，积分系数为 Ki=0.000 85。

把Gf(s)也选为PI控制器，用凑试法整定参数:比例系数 Kpf=0.17，积分系数 Kif=0.011。

干扰补偿器件的传递函数Wg(s)和Wc(s)对系统的抗干扰性能有较大影响。用试凑法整定得:

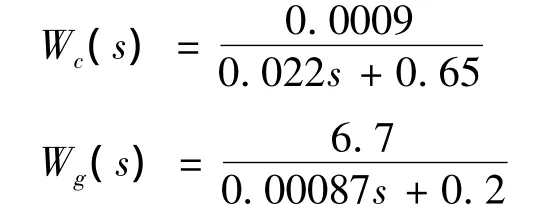
用simulink对本文的改进型Smith控制系统进行仿真研究，simulink仿真框图如图3。

图1所示控制系统的simulink框图，只须在图3的仿真框图中去掉Wc和Wg即可。经整定，失配补偿控制系统的主控制器参数为:比例系数为Kp1=0.11，积分系数为 Ki=0.008 5。Gf(s)的比例系数为 Kpf=0.17，积分系数为 Kif=0.011。

4 实例的simulink仿真结果

对图1所示的失配补偿Smith控制系统仿真，仿真时间为1 000 s。系统未受干扰时，系统输出曲线如图4。从仿真结果可知它没有稳态误差。

干扰信号的波形如图5所示。

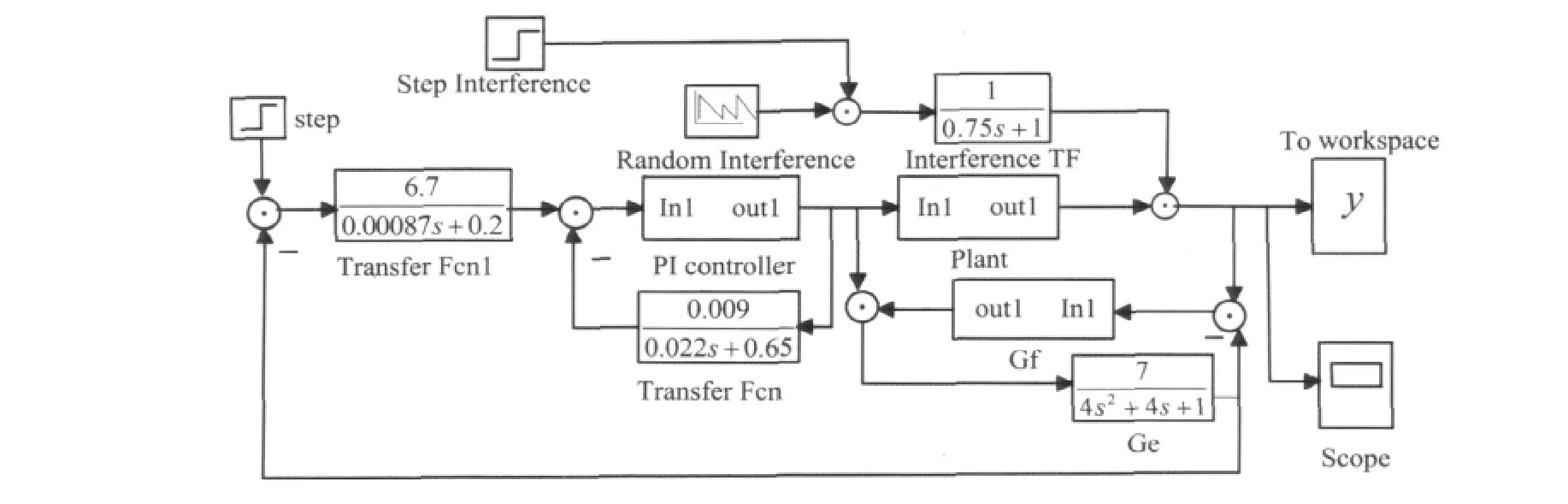
图3 本文的改进型Smith控制系统的仿真框图Fig.3 Simulation diagram of improved Smith control system in this paper

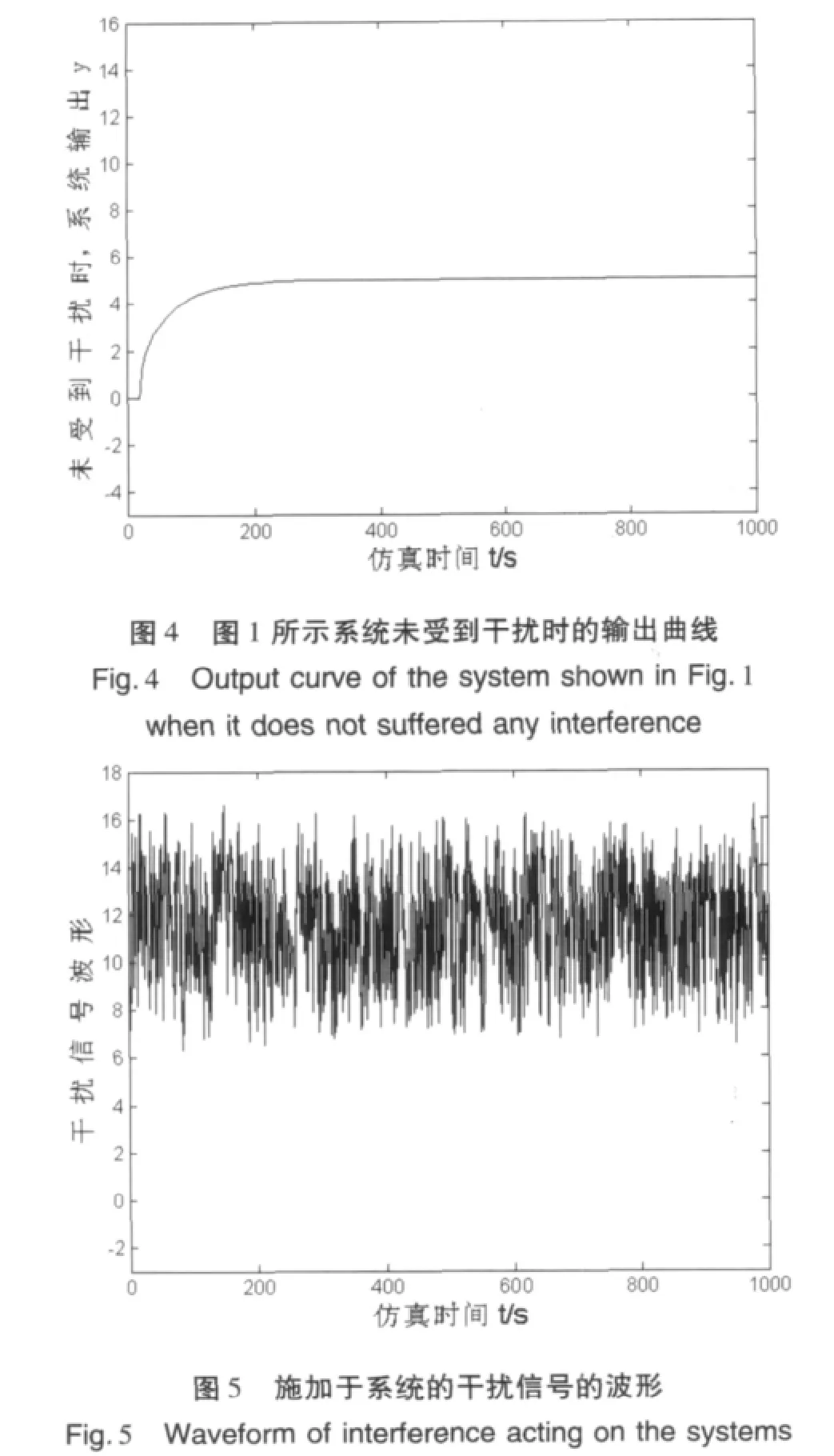
把图5所示的干扰施加于图1的控制系统，对该情况进行仿真;仿真时间1 000 s，系统的输出如图6。仿真时间20 000 s，系统的输出如图7。

把姜克君等(2011)的加了微分反馈的改进型Smith控制方法(以下简称为微分反馈Smith控制)应用于本文算例，仿真框图见图8。

图8中，预估器模型取为:

若不辨识对象的滞后时间，预估器模型取为:

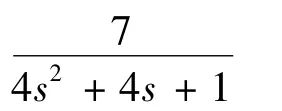
则无论怎样整定参数，都无法使系统稳定。

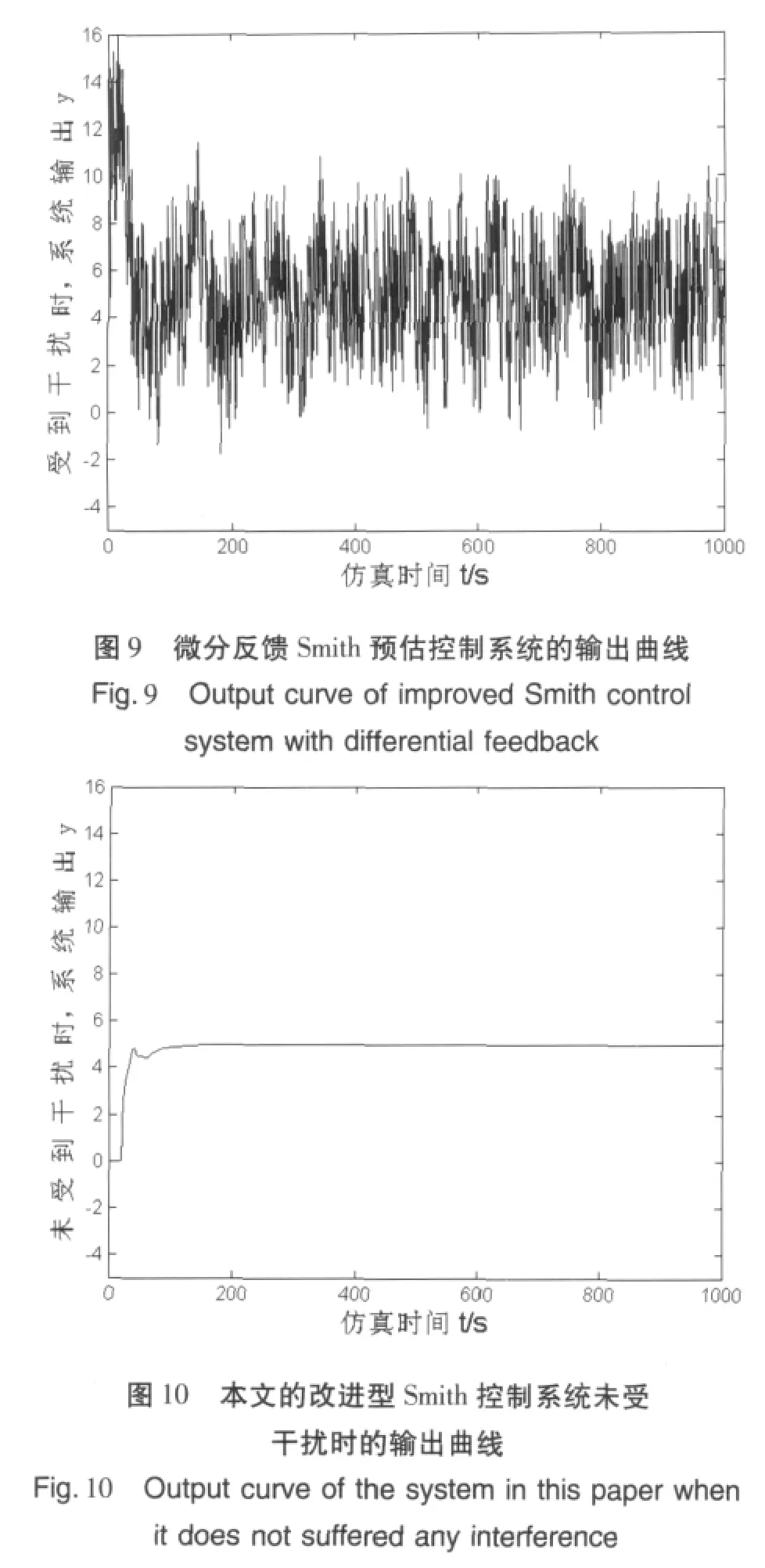
图8中，经整定，Kd取 0.000 55，PI控制器中Kp取0.001 1，Ki取0.026。仿真结果如图9。

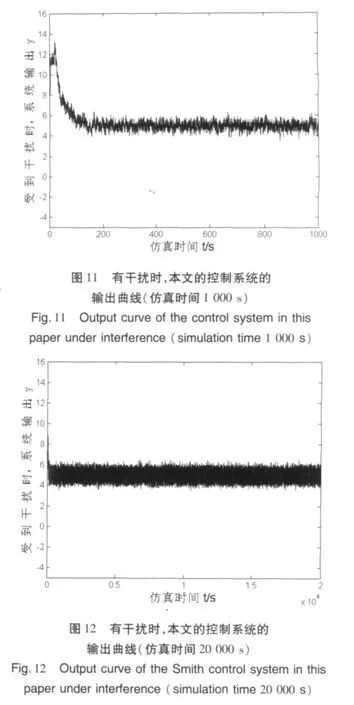
对本文的加了补偿器Wc(s)和Wg(s)的Smith控制系统使用图3的simulink框图进行仿真。先对系统未受干扰的情况进行仿真，所得结果如图10。

再对该控制系统加上图5所示的负载干扰后，进行Simulink仿真;仿真时间1 000 s的结果如图11所示，仿真时间20 000 s的结果如图12所示。

5 仿真结果分析

由仿真框图可知，失配补偿Smith控制系统和本文的改进型Smith控制系统中，控制器和补偿器都不含有被控对象的纯滞后时间τ，因此设计时不需要知道τ。理论上补偿器Ge(s)等于对象的Gp(s)时，控制效果最好。由图4和图10可见，实际上当Ge(s)和Gp(s)之间有较大误差时，在系统未受到干扰的情况下，两者的控制效果仍然很好。

由图6和图7所示的仿真结果可知，失配补偿Smith系统在受到较大的随机振荡的负载干扰时，控制性能较差。比较图5和图6可以发现，随机干扰作用于该系统后，系统输出的振荡幅度大约等于随机干扰的振荡幅度。当随机干扰振荡幅值较大时，系统将无法使用。这是这种控制器难以广泛使用的主要原因。

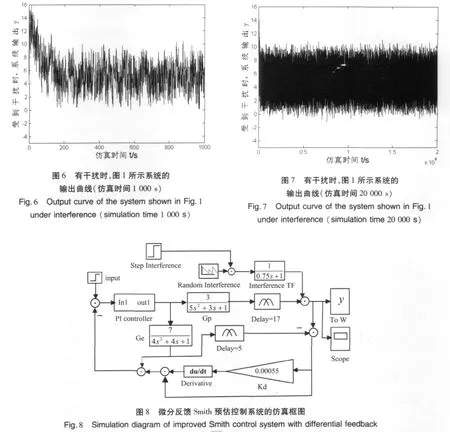
由图9可知，微分反馈Smith控制系统在受到较大的随机性的负载干扰时，其系统输出性能和失配补偿Smith控制系统基本上相同。但该系统的容错性能不如失配补偿Smith控制系统。

由图10可知，本文的改进型Smith控制系统在未受到干扰时，相比于失配补偿Smith控制系统，上升时间略有提高。稍有振荡，但不带来不良影响。

由图11和图12所示的仿真结果可见，本文的改进型Smith控制系统，在受到较大随机振荡负载干扰时，抗扰性能比失配补偿Smith控制系统和微分反馈Smith控制系统的抗扰性能优越得多。主要表现在系统输出方差大为减小，输出的振荡幅度比后两者者小得多，约为后两者的本文的Smith控制器改进了失配补偿Smith控制器等改进型smith控制器的主要缺点，解决了Smith控制器实用化的关键问题。

对其它实例作了仿真研究，得到了类似的仿真结果，限于篇幅不一一列举。

根据这些研究结果可以做出相应结论。

5 结论

本文提出了一种新的改进型Smith控制方法。它在失配补偿Smith控制系统基础上，增加了两个补偿环节。它对较强的随机性负载干扰有很好的抗干扰作用，克服了失配补偿Smith控制器的主要缺点。它容许预估器和对象模型有一定误差，所以降低了辨识被控对象的精度要求，而且不需要辨识被控对象的纯滞后时间。另外，它较为简单，容易实现。由于具有这些优点，本文的改进型Smith控制器有很好的应用价值，在化工、炼油、制药等过程的自动化设备中有其应用前景。

韩冰，韩敏.2010.基于动态BP算法的非线性滞后系统辨识[J].大连理工大学学报，50(5):777-781.

姜克君，戴丽红，郝睿，等.2011.Smith预估控制系统抗扰性能的改善[J].辽宁科技大学学报，34(5):480-485.

刘文定，王东林.2009.过程控制系统的MATLAB仿真[M].北京:机械工业出版社:234-235.

谢成清，夏洪，朱立.2011.基于RBF神经网络的自回归系统辨识模型[J].东华理工大学学报:自然科学版，34(4):392-395.

杨平，周贞.2010.论一种完全抗干扰Smith预估控制方案的可用性[J].化工自动化及仪表，37(5):13-15.

赵东亚，邹涛，王治平.2010.Smith预估控制研究进展[J].化工进展，29(8)，1406-1410.

Uma S，Chidambaram M，Rao Seshagiri A.2010.Set point weighted modified Smith predictor with PID filter controllers for non-minimumphase(NMP)integrating processes[J].Chemical Engineering Research and Design，88(55-56):592-601.